Non-Intrusive Parametrized-Background Data-Weak Reconstruction of Cardiac Displacement Fields from Sparse MRI-like Observations

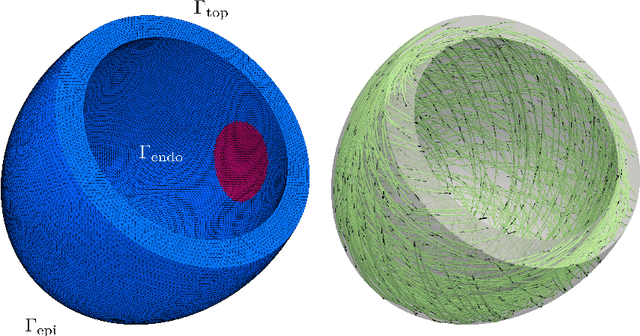
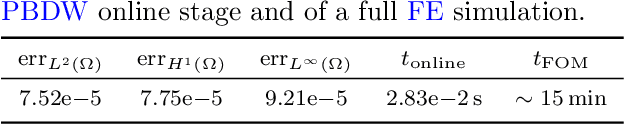
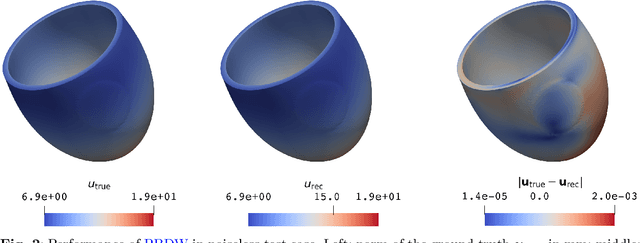
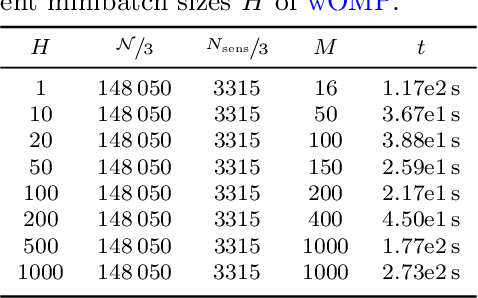
Personalized cardiac diagnostics require accurate reconstruction of myocardial displacement fields from sparse clinical imaging data, yet current methods often demand intrusive access to computational models. In this work, we apply the non-intrusive Parametrized-Background Data-Weak (PBDW) approach to three-dimensional (3D) cardiac displacement field reconstruction from limited Magnetic Resonance Image (MRI)-like observations. Our implementation requires only solution snapshots -- no governing equations, assembly routines, or solver access -- enabling immediate deployment across commercial and research codes using different constitutive models. Additionally, we introduce two enhancements: an H-size minibatch worst-case Orthogonal Matching Pursuit (wOMP) algorithm that improves Sensor Selection (SS) computational efficiency while maintaining reconstruction accuracy, and memory optimization techniques exploiting block matrix structures in vectorial problems. We demonstrate the effectiveness of the method through validation on a 3D left ventricular model with simulated scar tissue. Starting with noise-free reconstruction, we systematically incorporate Gaussian noise and spatial sparsity mimicking realistic MRI acquisition protocols. Results show exceptional accuracy in noise-free conditions (relative L2 error of order O(1e-5)), robust performance with 10% noise (relative L2 error of order O(1e-2)), and effective reconstruction from sparse measurements (relative L2 error of order O(1e-2)). The online reconstruction achieves four-order-of-magnitude computational speed-up compared to full Finite Element (FE) simulations, with reconstruction times under one tenth of second for sparse scenarios, demonstrating significant potential for integration into clinical cardiac modeling workflows.

CONSIGN: Conformal Segmentation Informed by Spatial Groupings via Decomposition

Most machine learning-based image segmentation models produce pixel-wise confidence scores - typically derived from softmax outputs - that represent the model's predicted probability for each class label at every pixel. While this information can be particularly valuable in high-stakes domains such as medical imaging, these (uncalibrated) scores are heuristic in nature and do not constitute rigorous quantitative uncertainty estimates. Conformal prediction (CP) provides a principled framework for transforming heuristic confidence scores into statistically valid uncertainty estimates. However, applying CP directly to image segmentation ignores the spatial correlations between pixels, a fundamental characteristic of image data. This can result in overly conservative and less interpretable uncertainty estimates. To address this, we propose CONSIGN (Conformal Segmentation Informed by Spatial Groupings via Decomposition), a CP-based method that incorporates spatial correlations to improve uncertainty quantification in image segmentation. Our method generates meaningful prediction sets that come with user-specified, high-probability error guarantees. It is compatible with any pre-trained segmentation model capable of generating multiple sample outputs - such as those using dropout, Bayesian modeling, or ensembles. We evaluate CONSIGN against a standard pixel-wise CP approach across three medical imaging datasets and two COCO dataset subsets, using three different pre-trained segmentation models. Results demonstrate that accounting for spatial structure significantly improves performance across multiple metrics and enhances the quality of uncertainty estimates.

Gaussian Process Emulators for Few-Shot Segmentation in Cardiac MRI

Segmentation of cardiac magnetic resonance images (MRI) is crucial for the analysis and assessment of cardiac function, helping to diagnose and treat various cardiovascular diseases. Most recent techniques rely on deep learning and usually require an extensive amount of labeled data. To overcome this problem, few-shot learning has the capability of reducing data dependency on labeled data. In this work, we introduce a new method that merges few-shot learning with a U-Net architecture and Gaussian Process Emulators (GPEs), enhancing data integration from a support set for improved performance. GPEs are trained to learn the relation between the support images and the corresponding masks in latent space, facilitating the segmentation of unseen query images given only a small labeled support set at inference. We test our model with the M&Ms-2 public dataset to assess its ability to segment the heart in cardiac magnetic resonance imaging from different orientations, and compare it with state-of-the-art unsupervised and few-shot methods. Our architecture shows higher DICE coefficients compared to these methods, especially in the more challenging setups where the size of the support set is considerably small.

Physics-informed Neural Network Estimation of Material Properties in Soft Tissue Nonlinear Biomechanical Models

The development of biophysical models for clinical applications is rapidly advancing in the research community, thanks to their predictive nature and their ability to assist the interpretation of clinical data. However, high-resolution and accurate multi-physics computational models are computationally expensive and their personalisation involves fine calibration of a large number of parameters, which may be space-dependent, challenging their clinical translation. In this work, we propose a new approach which relies on the combination of physics-informed neural networks (PINNs) with three-dimensional soft tissue nonlinear biomechanical models, capable of reconstructing displacement fields and estimating heterogeneous patient-specific biophysical properties. The proposed learning algorithm encodes information from a limited amount of displacement and, in some cases, strain data, that can be routinely acquired in the clinical setting, and combines it with the physics of the problem, represented by a mathematical model based on partial differential equations, to regularise the problem and improve its convergence properties. Several benchmarks are presented to show the accuracy and robustness of the proposed method and its great potential to enable the robust and effective identification of patient-specific, heterogeneous physical properties, s.a. tissue stiffness properties. In particular, we demonstrate the capability of the PINN to detect the presence, location and severity of scar tissue, which is beneficial to develop personalised simulation models for disease diagnosis, especially for cardiac applications.