Physics-informed Neural Network Estimation of Material Properties in Soft Tissue Nonlinear Biomechanical Models

The development of biophysical models for clinical applications is rapidly advancing in the research community, thanks to their predictive nature and their ability to assist the interpretation of clinical data. However, high-resolution and accurate multi-physics computational models are computationally expensive and their personalisation involves fine calibration of a large number of parameters, which may be space-dependent, challenging their clinical translation. In this work, we propose a new approach which relies on the combination of physics-informed neural networks (PINNs) with three-dimensional soft tissue nonlinear biomechanical models, capable of reconstructing displacement fields and estimating heterogeneous patient-specific biophysical properties. The proposed learning algorithm encodes information from a limited amount of displacement and, in some cases, strain data, that can be routinely acquired in the clinical setting, and combines it with the physics of the problem, represented by a mathematical model based on partial differential equations, to regularise the problem and improve its convergence properties. Several benchmarks are presented to show the accuracy and robustness of the proposed method and its great potential to enable the robust and effective identification of patient-specific, heterogeneous physical properties, s.a. tissue stiffness properties. In particular, we demonstrate the capability of the PINN to detect the presence, location and severity of scar tissue, which is beneficial to develop personalised simulation models for disease diagnosis, especially for cardiac applications.

Real-time whole-heart electromechanical simulations using Latent Neural Ordinary Differential Equations

Cardiac digital twins provide a physics and physiology informed framework to deliver predictive and personalized medicine. However, high-fidelity multi-scale cardiac models remain a barrier to adoption due to their extensive computational costs and the high number of model evaluations needed for patient-specific personalization. Artificial Intelligence-based methods can make the creation of fast and accurate whole-heart digital twins feasible. In this work, we use Latent Neural Ordinary Differential Equations (LNODEs) to learn the temporal pressure-volume dynamics of a heart failure patient. Our surrogate model based on LNODEs is trained from 400 3D-0D whole-heart closed-loop electromechanical simulations while accounting for 43 model parameters, describing single cell through to whole organ and cardiovascular hemodynamics. The trained LNODEs provides a compact and efficient representation of the 3D-0D model in a latent space by means of a feedforward fully-connected Artificial Neural Network that retains 3 hidden layers with 13 neurons per layer and allows for 300x real-time numerical simulations of the cardiac function on a single processor of a standard laptop. This surrogate model is employed to perform global sensitivity analysis and robust parameter estimation with uncertainty quantification in 3 hours of computations, still on a single processor. We match pressure and volume time traces unseen by the LNODEs during the training phase and we calibrate 4 to 11 model parameters while also providing their posterior distribution. This paper introduces the most advanced surrogate model of cardiac function available in the literature and opens new important venues for parameter calibration in cardiac digital twins.

Latent Dynamics Networks (LDNets): learning the intrinsic dynamics of spatio-temporal processes

Predicting the evolution of systems that exhibit spatio-temporal dynamics in response to external stimuli is a key enabling technology fostering scientific innovation. Traditional equations-based approaches leverage first principles to yield predictions through the numerical approximation of high-dimensional systems of differential equations, thus calling for large-scale parallel computing platforms and requiring large computational costs. Data-driven approaches, instead, enable the description of systems evolution in low-dimensional latent spaces, by leveraging dimensionality reduction and deep learning algorithms. We propose a novel architecture, named Latent Dynamics Network (LDNet), which is able to discover low-dimensional intrinsic dynamics of possibly non-Markovian dynamical systems, thus predicting the time evolution of space-dependent fields in response to external inputs. Unlike popular approaches, in which the latent representation of the solution manifold is learned by means of auto-encoders that map a high-dimensional discretization of the system state into itself, LDNets automatically discover a low-dimensional manifold while learning the latent dynamics, without ever operating in the high-dimensional space. Furthermore, LDNets are meshless algorithms that do not reconstruct the output on a predetermined grid of points, but rather at any point of the domain, thus enabling weight-sharing across query-points. These features make LDNets lightweight and easy-to-train, with excellent accuracy and generalization properties, even in time-extrapolation regimes. We validate our method on several test cases and we show that, for a challenging highly-nonlinear problem, LDNets outperform state-of-the-art methods in terms of accuracy (normalized error 5 times smaller), by employing a dramatically smaller number of trainable parameters (more than 10 times fewer).

Deep learning-based reduced order models in cardiac electrophysiology

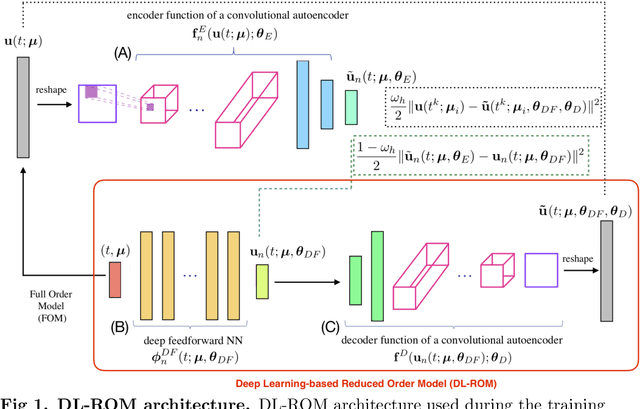
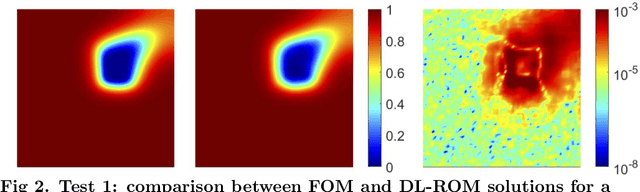
Predicting the electrical behavior of the heart, from the cellular scale to the tissue level, relies on the formulation and numerical approximation of coupled nonlinear dynamical systems. These systems describe the cardiac action potential, that is the polarization/depolarization cycle occurring at every heart beat that models the time evolution of the electrical potential across the cell membrane, as well as a set of ionic variables. Multiple solutions of these systems, corresponding to different model inputs, are required to evaluate outputs of clinical interest, such as activation maps and action potential duration. More importantly, these models feature coherent structures that propagate over time, such as wavefronts. These systems can hardly be reduced to lower dimensional problems by conventional reduced order models (ROMs) such as, e.g., the reduced basis (RB) method. This is primarily due to the low regularity of the solution manifold (with respect to the problem parameters) as well as to the nonlinear nature of the input-output maps that we intend to reconstruct numerically. To overcome this difficulty, in this paper we propose a new, nonlinear approach which exploits deep learning (DL) algorithms to obtain accurate and efficient ROMs, whose dimensionality matches the number of system parameters. Our DL approach combines deep feedforward neural networks (NNs) and convolutional autoencoders (AEs). We show that the proposed DL-ROM framework can efficiently provide solutions to parametrized electrophysiology problems, thus enabling multi-scenario analysis in pathological cases. We investigate three challenging test cases in cardiac electrophysiology and prove that DL-ROM outperforms classical projection-based ROMs.