Gaussian Process Emulators for Few-Shot Segmentation in Cardiac MRI

Segmentation of cardiac magnetic resonance images (MRI) is crucial for the analysis and assessment of cardiac function, helping to diagnose and treat various cardiovascular diseases. Most recent techniques rely on deep learning and usually require an extensive amount of labeled data. To overcome this problem, few-shot learning has the capability of reducing data dependency on labeled data. In this work, we introduce a new method that merges few-shot learning with a U-Net architecture and Gaussian Process Emulators (GPEs), enhancing data integration from a support set for improved performance. GPEs are trained to learn the relation between the support images and the corresponding masks in latent space, facilitating the segmentation of unseen query images given only a small labeled support set at inference. We test our model with the M&Ms-2 public dataset to assess its ability to segment the heart in cardiac magnetic resonance imaging from different orientations, and compare it with state-of-the-art unsupervised and few-shot methods. Our architecture shows higher DICE coefficients compared to these methods, especially in the more challenging setups where the size of the support set is considerably small.

On uniqueness in structured model learning

This paper addresses the problem of uniqueness in learning physical laws for systems of partial differential equations (PDEs). Contrary to most existing approaches, it considers a framework of structured model learning, where existing, approximately correct physical models are augmented with components that are learned from data. The main result of the paper is a uniqueness result that covers a large class of PDEs and a suitable class of neural networks used for approximating the unknown model components. The uniqueness result shows that, in the idealized setting of full, noiseless measurements, a unique identification of the unknown model components is possible as regularization-minimizing solution of the PDE system. Furthermore, the paper provides a convergence result showing that model components learned on the basis of incomplete, noisy measurements approximate the ground truth model component in the limit. These results are possible under specific properties of the approximating neural networks and due to a dedicated choice of regularization. With this, a practical contribution of this analytic paper is to provide a class of model learning frameworks different to standard settings where uniqueness can be expected in the limit of full measurements.

On the growth of the parameters of approximating ReLU neural networks

This work focuses on the analysis of fully connected feed forward ReLU neural networks as they approximate a given, smooth function. In contrast to conventionally studied universal approximation properties under increasing architectures, e.g., in terms of width or depth of the networks, we are concerned with the asymptotic growth of the parameters of approximating networks. Such results are of interest, e.g., for error analysis or consistency results for neural network training. The main result of our work is that, for a ReLU architecture with state of the art approximation error, the realizing parameters grow at most polynomially. The obtained rate with respect to a normalized network size is compared to existing results and is shown to be superior in most cases, in particular for high dimensional input.

Neural-network-based regularization methods for inverse problems in imaging

This review provides an introduction to - and overview of - the current state of the art in neural-network based regularization methods for inverse problems in imaging. It aims to introduce readers with a solid knowledge in applied mathematics and a basic understanding of neural networks to different concepts of applying neural networks for regularizing inverse problems in imaging. Distinguishing features of this review are, among others, an easily accessible introduction to learned generators and learned priors, in particular diffusion models, for inverse problems, and a section focusing explicitly on existing results in function space analysis of neural-network-based approaches in this context.

Posterior-Variance-Based Error Quantification for Inverse Problems in Imaging

In this work, a method for obtaining pixel-wise error bounds in Bayesian regularization of inverse imaging problems is introduced. The proposed method employs estimates of the posterior variance together with techniques from conformal prediction in order to obtain coverage guarantees for the error bounds, without making any assumption on the underlying data distribution. It is generally applicable to Bayesian regularization approaches, independent, e.g., of the concrete choice of the prior. Furthermore, the coverage guarantees can also be obtained in case only approximate sampling from the posterior is possible. With this in particular, the proposed framework is able to incorporate any learned prior in a black-box manner. Guaranteed coverage without assumptions on the underlying distributions is only achievable since the magnitude of the error bounds is, in general, unknown in advance. Nevertheless, experiments with multiple regularization approaches presented in the paper confirm that in practice, the obtained error bounds are rather tight. For realizing the numerical experiments, also a novel primal-dual Langevin algorithm for sampling from non-smooth distributions is introduced in this work.

Unsupervised energy disaggregation via convolutional sparse coding

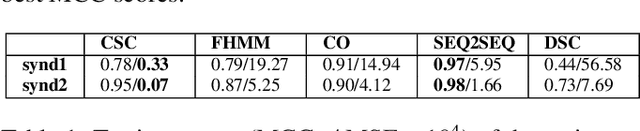
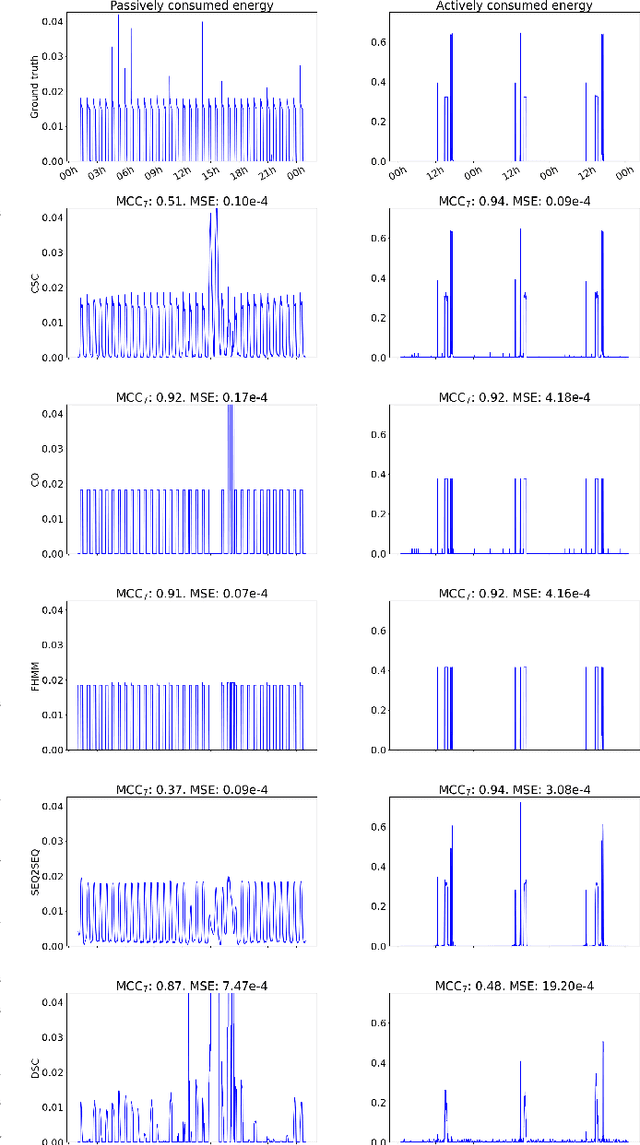
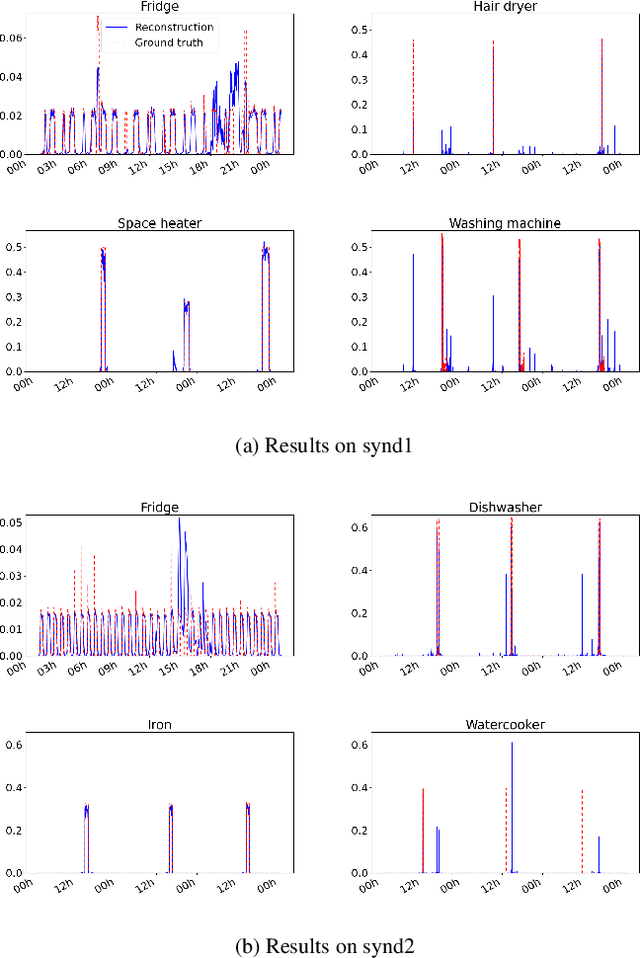
In this work, a method for unsupervised energy disaggregation in private households equipped with smart meters is proposed. This method aims to classify power consumption as active or passive, granting the ability to report on the residents' activity and presence without direct interaction. This lays the foundation for applications like non-intrusive health monitoring of private homes. The proposed method is based on minimizing a suitable energy functional, for which the iPALM (inertial proximal alternating linearized minimization) algorithm is employed, demonstrating that various conditions guaranteeing convergence are satisfied. In order to confirm feasibility of the proposed method, experiments on semi-synthetic test data sets and a comparison to existing, supervised methods are provided.

Nonlinear motion separation via untrained generator networks with disentangled latent space variables and applications to cardiac MRI

In this paper, a nonlinear approach to separate different motion types in video data is proposed. This is particularly relevant in dynamic medical imaging (e.g. PET, MRI), where patient motion poses a significant challenge due to its effects on the image reconstruction as well as for its subsequent interpretation. Here, a new method is proposed where dynamic images are represented as the forward mapping of a sequence of latent variables via a generator neural network. The latent variables are structured so that temporal variations in the data are represented via dynamic latent variables, which are independent of static latent variables characterizing the general structure of the frames. In particular, different kinds of motion are also characterized independently of each other via latent space disentanglement using one-dimensional prior information on all but one of the motion types. This representation allows to freeze any selection of motion types, and to obtain accurate independent representations of other dynamics of interest. Moreover, the proposed algorithm is training-free, i.e., all the network parameters are learned directly from a single video. We illustrate the performance of this method on phantom and real-data MRI examples, where we successfully separate respiratory and cardiac motion.

Accelerometry-based classification of circulatory states during out-of-hospital cardiac arrest

Objective: During cardiac arrest treatment, a reliable detection of spontaneous circulation, usually performed by manual pulse checks, is both vital for patient survival and practically challenging. Methods: We developed a machine learning algorithm to automatically predict the circulatory state during cardiac arrest treatment from 4-second-long snippets of accelerometry and electrocardiogram data from real-world defibrillator records. The algorithm was trained based on 917 cases from the German Resuscitation Registry, for which ground truth labels were created by a manual annotation of physicians. It uses a kernelized Support Vector Machine classifier based on 14 features, which partially reflect the correlation between accelerometry and electrocardiogram data. Results: On a test data set, the proposed algorithm exhibits an accuracy of 94.4 (93.6, 95.2)%, a sensitivity of 95.0 (93.9, 96.1)%, and a specificity of 93.9 (92.7, 95.1)%. Conclusion and significance: In application, the algorithm may be used to simplify retrospective annotation for quality management and, moreover, to support clinicians to assess circulatory state during cardiac arrest treatment.

A Note on the Regularity of Images Generated by Convolutional Neural Networks

The regularity of images generated by convolutional neural networks, such as the U-net, generative adversarial networks, or the deep image prior, is analyzed. In a resolution-independent, infinite dimensional setting, it is shown that such images, represented as functions, are always continuous and, in some circumstances, even continuously differentiable, contradicting the widely accepted modeling of sharp edges in images via jump discontinuities. While such statements require an infinite dimensional setting, the connection to (discretized) neural networks used in practice is made by considering the limit as the resolution approaches infinity. As practical consequence, the results of this paper suggest to refrain from basic L2 regularization of network weights in case of images being the network output.