Neural-network-based regularization methods for inverse problems in imaging

This review provides an introduction to - and overview of - the current state of the art in neural-network based regularization methods for inverse problems in imaging. It aims to introduce readers with a solid knowledge in applied mathematics and a basic understanding of neural networks to different concepts of applying neural networks for regularizing inverse problems in imaging. Distinguishing features of this review are, among others, an easily accessible introduction to learned generators and learned priors, in particular diffusion models, for inverse problems, and a section focusing explicitly on existing results in function space analysis of neural-network-based approaches in this context.

Posterior-Variance-Based Error Quantification for Inverse Problems in Imaging

In this work, a method for obtaining pixel-wise error bounds in Bayesian regularization of inverse imaging problems is introduced. The proposed method employs estimates of the posterior variance together with techniques from conformal prediction in order to obtain coverage guarantees for the error bounds, without making any assumption on the underlying data distribution. It is generally applicable to Bayesian regularization approaches, independent, e.g., of the concrete choice of the prior. Furthermore, the coverage guarantees can also be obtained in case only approximate sampling from the posterior is possible. With this in particular, the proposed framework is able to incorporate any learned prior in a black-box manner. Guaranteed coverage without assumptions on the underlying distributions is only achievable since the magnitude of the error bounds is, in general, unknown in advance. Nevertheless, experiments with multiple regularization approaches presented in the paper confirm that in practice, the obtained error bounds are rather tight. For realizing the numerical experiments, also a novel primal-dual Langevin algorithm for sampling from non-smooth distributions is introduced in this work.

Unsupervised energy disaggregation via convolutional sparse coding

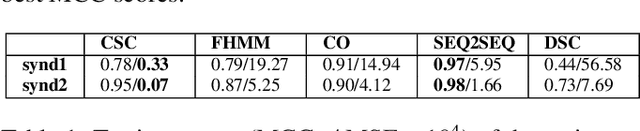
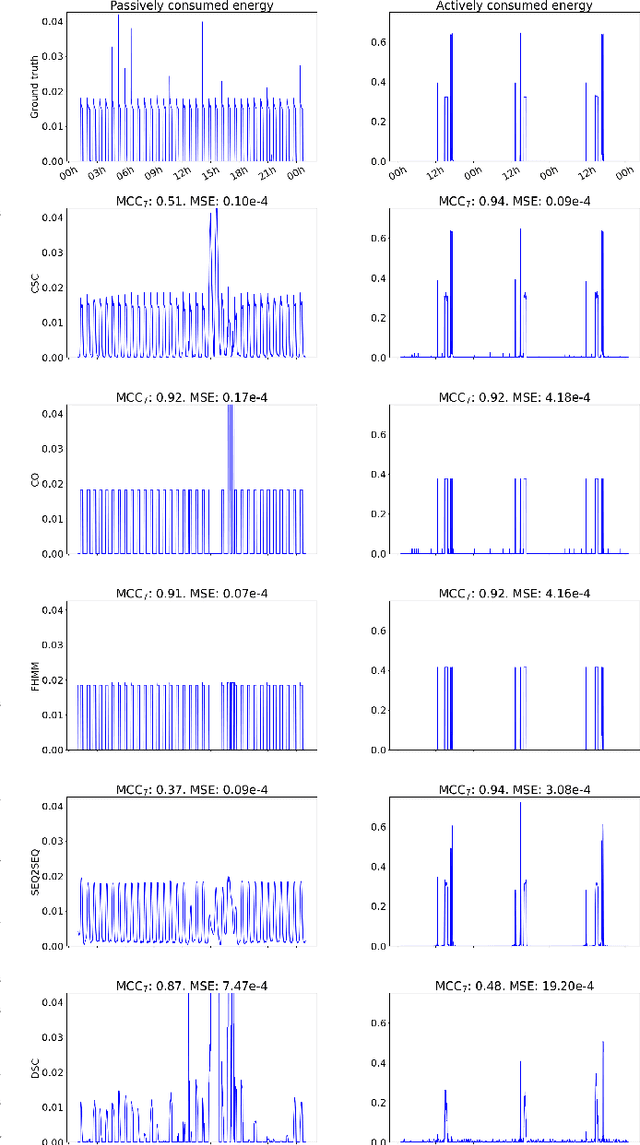
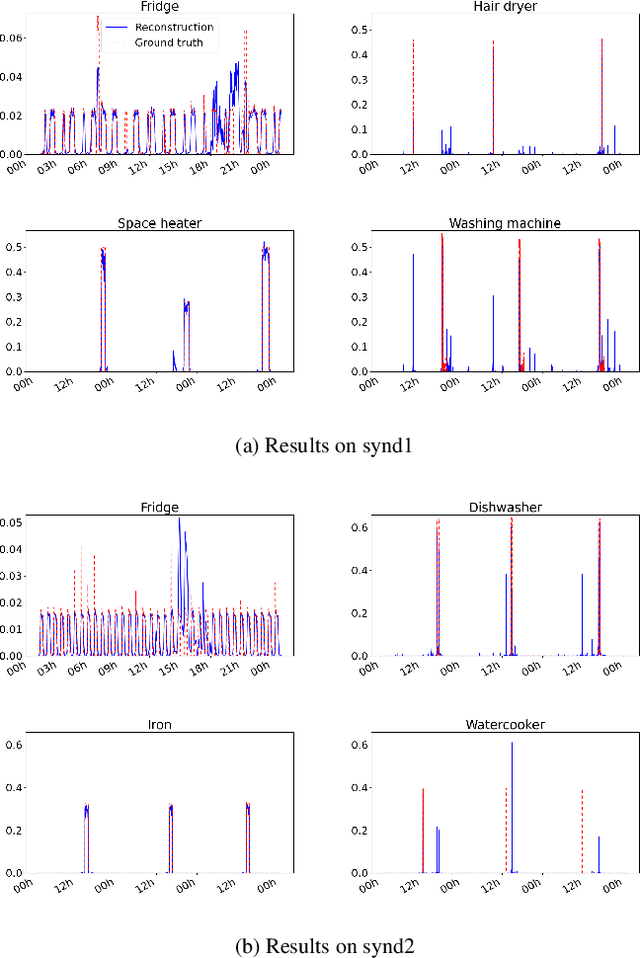
In this work, a method for unsupervised energy disaggregation in private households equipped with smart meters is proposed. This method aims to classify power consumption as active or passive, granting the ability to report on the residents' activity and presence without direct interaction. This lays the foundation for applications like non-intrusive health monitoring of private homes. The proposed method is based on minimizing a suitable energy functional, for which the iPALM (inertial proximal alternating linearized minimization) algorithm is employed, demonstrating that various conditions guaranteeing convergence are satisfied. In order to confirm feasibility of the proposed method, experiments on semi-synthetic test data sets and a comparison to existing, supervised methods are provided.

A Note on the Regularity of Images Generated by Convolutional Neural Networks

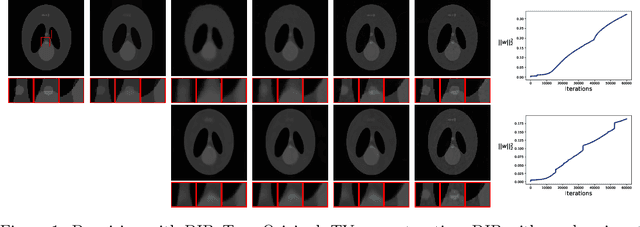
The regularity of images generated by convolutional neural networks, such as the U-net, generative adversarial networks, or the deep image prior, is analyzed. In a resolution-independent, infinite dimensional setting, it is shown that such images, represented as functions, are always continuous and, in some circumstances, even continuously differentiable, contradicting the widely accepted modeling of sharp edges in images via jump discontinuities. While such statements require an infinite dimensional setting, the connection to (discretized) neural networks used in practice is made by considering the limit as the resolution approaches infinity. As practical consequence, the results of this paper suggest to refrain from basic L2 regularization of network weights in case of images being the network output.