The Gaussian Latent Machine: Efficient Prior and Posterior Sampling for Inverse Problems

We consider the problem of sampling from a product-of-experts-type model that encompasses many standard prior and posterior distributions commonly found in Bayesian imaging. We show that this model can be easily lifted into a novel latent variable model, which we refer to as a Gaussian latent machine. This leads to a general sampling approach that unifies and generalizes many existing sampling algorithms in the literature. Most notably, it yields a highly efficient and effective two-block Gibbs sampling approach in the general case, while also specializing to direct sampling algorithms in particular cases. Finally, we present detailed numerical experiments that demonstrate the efficiency and effectiveness of our proposed sampling approach across a wide range of prior and posterior sampling problems from Bayesian imaging.

Product of Gaussian Mixture Diffusion Model for non-linear MRI Inversion

Diffusion models have recently shown remarkable results in magnetic resonance imaging reconstruction. However, the employed networks typically are black-box estimators of the (smoothed) prior score with tens of millions of parameters, restricting interpretability and increasing reconstruction time. Furthermore, parallel imaging reconstruction algorithms either rely on off-line coil sensitivity estimation, which is prone to misalignment and restricting sampling trajectories, or perform per-coil reconstruction, making the computational cost proportional to the number of coils. To overcome this, we jointly reconstruct the image and the coil sensitivities using the lightweight, parameter-efficient, and interpretable product of Gaussian mixture diffusion model as an image prior and a classical smoothness priors on the coil sensitivities. The proposed method delivers promising results while allowing for fast inference and demonstrating robustness to contrast out-of-distribution data and sampling trajectories, comparable to classical variational penalties such as total variation. Finally, the probabilistic formulation allows the calculation of the posterior expectation and pixel-wise variance.

Bigger Isn't Always Better: Towards a General Prior for Medical Image Reconstruction

Diffusion model have been successfully applied to many inverse problems, including MRI and CT reconstruction. Researchers typically re-purpose models originally designed for unconditional sampling without modifications. Using two different posterior sampling algorithms, we show empirically that such large networks are not necessary. Our smallest model, effectively a ResNet, performs almost as good as an attention U-Net on in-distribution reconstruction, while being significantly more robust towards distribution shifts. Furthermore, we introduce models trained on natural images and demonstrate that they can be used in both MRI and CT reconstruction, out-performing model trained on medical images in out-of-distribution cases. As a result of our findings, we strongly caution against simply re-using very large networks and encourage researchers to adapt the model complexity to the respective task. Moreover, we argue that a key step towards a general diffusion-based prior is training on natural images.

GMM-IKRS: Gaussian Mixture Models for Interpretable Keypoint Refinement and Scoring

The extraction of keypoints in images is at the basis of many computer vision applications, from localization to 3D reconstruction. Keypoints come with a score permitting to rank them according to their quality. While learned keypoints often exhibit better properties than handcrafted ones, their scores are not easily interpretable, making it virtually impossible to compare the quality of individual keypoints across methods. We propose a framework that can refine, and at the same time characterize with an interpretable score, the keypoints extracted by any method. Our approach leverages a modified robust Gaussian Mixture Model fit designed to both reject non-robust keypoints and refine the remaining ones. Our score comprises two components: one relates to the probability of extracting the same keypoint in an image captured from another viewpoint, the other relates to the localization accuracy of the keypoint. These two interpretable components permit a comparison of individual keypoints extracted across different methods. Through extensive experiments we demonstrate that, when applied to popular keypoint detectors, our framework consistently improves the repeatability of keypoints as well as their performance in homography and two/multiple-view pose recovery tasks.

Joint Non-Linear MRI Inversion with Diffusion Priors

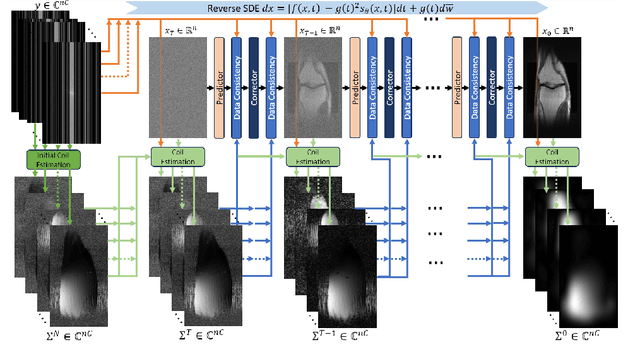
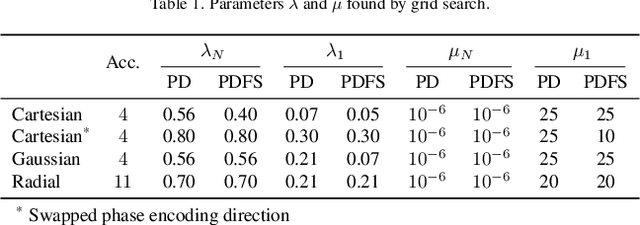
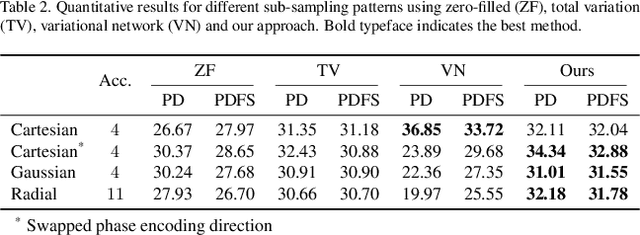
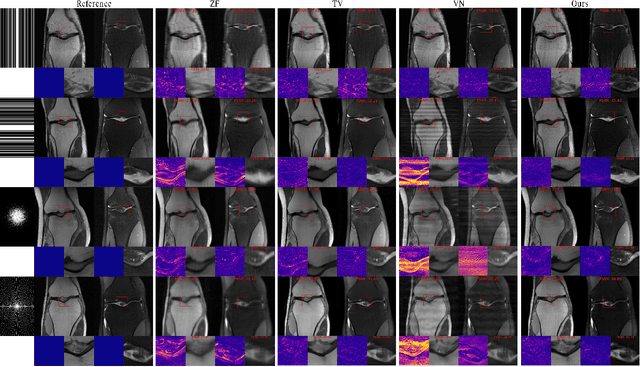
Magnetic resonance imaging (MRI) is a potent diagnostic tool, but suffers from long examination times. To accelerate the process, modern MRI machines typically utilize multiple coils that acquire sub-sampled data in parallel. Data-driven reconstruction approaches, in particular diffusion models, recently achieved remarkable success in reconstructing these data, but typically rely on estimating the coil sensitivities in an off-line step. This suffers from potential movement and misalignment artifacts and limits the application to Cartesian sampling trajectories. To obviate the need for off-line sensitivity estimation, we propose to jointly estimate the sensitivity maps with the image. In particular, we utilize a diffusion model -- trained on magnitude images only -- to generate high-fidelity images while imposing spatial smoothness of the sensitivity maps in the reverse diffusion. The proposed approach demonstrates consistent qualitative and quantitative performance across different sub-sampling patterns. In addition, experiments indicate a good fit of the estimated coil sensitivities.

Product of Gaussian Mixture Diffusion Models

In this work we tackle the problem of estimating the density $ f_X $ of a random variable $ X $ by successive smoothing, such that the smoothed random variable $ Y $ fulfills the diffusion partial differential equation $ (\partial_t - \Delta_1)f_Y(\,\cdot\,, t) = 0 $ with initial condition $ f_Y(\,\cdot\,, 0) = f_X $. We propose a product-of-experts-type model utilizing Gaussian mixture experts and study configurations that admit an analytic expression for $ f_Y (\,\cdot\,, t) $. In particular, with a focus on image processing, we derive conditions for models acting on filter-, wavelet-, and shearlet responses. Our construction naturally allows the model to be trained simultaneously over the entire diffusion horizon using empirical Bayes. We show numerical results for image denoising where our models are competitive while being tractable, interpretable, and having only a small number of learnable parameters. As a byproduct, our models can be used for reliable noise estimation, allowing blind denoising of images corrupted by heteroscedastic noise.

Explicit Diffusion of Gaussian Mixture Model Based Image Priors

In this work we tackle the problem of estimating the density $f_X$ of a random variable $X$ by successive smoothing, such that the smoothed random variable $Y$ fulfills $(\partial_t - \Delta_1)f_Y(\,\cdot\,, t) = 0$, $f_Y(\,\cdot\,, 0) = f_X$. With a focus on image processing, we propose a product/fields of experts model with Gaussian mixture experts that admits an analytic expression for $f_Y (\,\cdot\,, t)$ under an orthogonality constraint on the filters. This construction naturally allows the model to be trained simultaneously over the entire diffusion horizon using empirical Bayes. We show preliminary results on image denoising where our model leads to competitive results while being tractable, interpretable, and having only a small number of learnable parameters. As a byproduct, our model can be used for reliable noise estimation, allowing blind denoising of images corrupted by heteroscedastic noise.

Stable deep MRI reconstruction using Generative Priors

Data-driven approaches recently achieved remarkable success in medical image reconstruction, but integration into clinical routine remains challenging due to a lack of generalizability and interpretability. Existing approaches usually require high-quality data-image pairs for training, but such data is not easily available for any imaging protocol and the reconstruction quality can quickly degrade even if only minor changes are made to the protocol. In addition, data-driven methods may create artificial features that can influence the clinicians decision-making. This is unacceptable if the clinician is unaware of the uncertainty associated with the reconstruction. In this paper, we address these challenges in a unified framework based on generative image priors. We propose a novel deep neural network based regularizer which is trained in an unsupervised setting on reference images without requiring any data-image pairs. After training, the regularizer can be used as part of a classical variational approach in combination with any acquisition protocols and shows stable behavior even if the test data deviates significantly from the training data. Furthermore, our probabilistic interpretation provides a distribution of reconstructions and hence allows uncertainty quantification. We demonstrate our approach on parallel magnetic resonance imaging, where results show competitive performance with SotA end-to-end deep learning methods, while preserving the flexibility of the acquisition protocol and allowing for uncertainty quantification.

Computed Tomography Reconstruction using Generative Energy-Based Priors

In the past decades, Computed Tomography (CT) has established itself as one of the most important imaging techniques in medicine. Today, the applicability of CT is only limited by the deposited radiation dose, reduction of which manifests in noisy or incomplete measurements. Thus, the need for robust reconstruction algorithms arises. In this work, we learn a parametric regularizer with a global receptive field by maximizing it's likelihood on reference CT data. Due to this unsupervised learning strategy, our trained regularizer truly represents higher-level domain statistics, which we empirically demonstrate by synthesizing CT images. Moreover, this regularizer can easily be applied to different CT reconstruction problems by embedding it in a variational framework, which increases flexibility and interpretability compared to feed-forward learning-based approaches. In addition, the accompanying probabilistic perspective enables experts to explore the full posterior distribution and may quantify uncertainty of the reconstruction approach. We apply the regularizer to limited-angle and few-view CT reconstruction problems, where it outperforms traditional reconstruction algorithms by a large margin.