Construction of Grid Operators for Multilevel Solvers: a Neural Network Approach
Paper and Code
Sep 13, 2021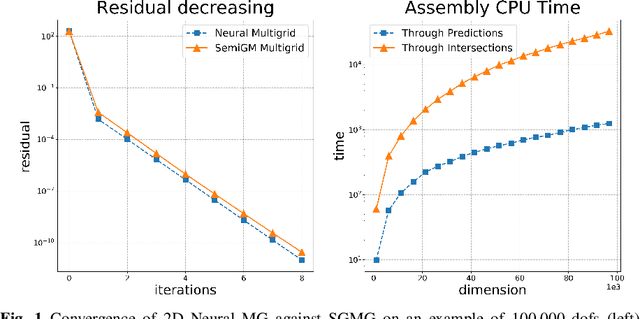
In this paper, we investigate the combination of multigrid methods and neural networks, starting from a Finite Element discretization of an elliptic PDE. Multigrid methods use interpolation operators to transfer information between different levels of approximation. These operators are crucial for fast convergence of multigrid, but they are generally unknown. We propose Deep Neural Network models for learning interpolation operators and we build a multilevel hierarchy based on the output of the network. We investigate the accuracy of the interpolation operator predicted by the Neural Network, testing it with different network architectures. This Neural Network approach for the construction of grid operators can then be extended for an automatic definition of multilevel solvers, allowing a portable solution in scientific computing
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge