Reward Redistribution for CVaR MDPs using a Bellman Operator on L-infinity

Tail-end risk measures such as static conditional value-at-risk (CVaR) are used in safety-critical applications to prevent rare, yet catastrophic events. Unlike risk-neutral objectives, the static CVaR of the return depends on entire trajectories without admitting a recursive Bellman decomposition in the underlying Markov decision process. A classical resolution relies on state augmentation with a continuous variable. However, unless restricted to a specialized class of admissible value functions, this formulation induces sparse rewards and degenerate fixed points. In this work, we propose a novel formulation of the static CVaR objective based on augmentation. Our alternative approach leads to a Bellman operator with: (1) dense per-step rewards; (2) contracting properties on the full space of bounded value functions. Building on this theoretical foundation, we develop risk-averse value iteration and model-free Q-learning algorithms that rely on discretized augmented states. We further provide convergence guarantees and approximation error bounds due to discretization. Empirical results demonstrate that our algorithms successfully learn CVaR-sensitive policies and achieve effective performance-safety trade-offs.

Designing Biological Sequences via Meta-Reinforcement Learning and Bayesian Optimization

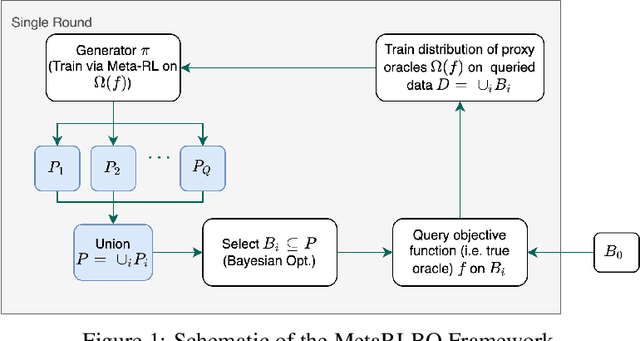
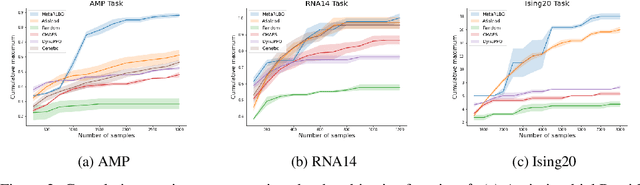
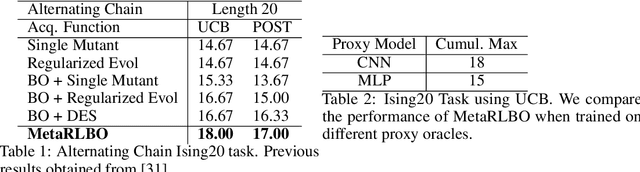
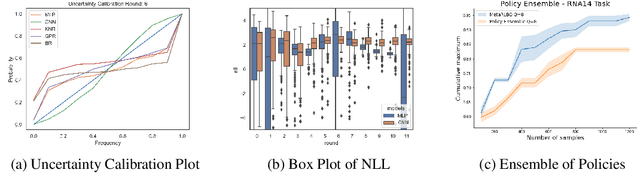
The ability to accelerate the design of biological sequences can have a substantial impact on the progress of the medical field. The problem can be framed as a global optimization problem where the objective is an expensive black-box function such that we can query large batches restricted with a limitation of a low number of rounds. Bayesian Optimization is a principled method for tackling this problem. However, the astronomically large state space of biological sequences renders brute-force iterating over all possible sequences infeasible. In this paper, we propose MetaRLBO where we train an autoregressive generative model via Meta-Reinforcement Learning to propose promising sequences for selection via Bayesian Optimization. We pose this problem as that of finding an optimal policy over a distribution of MDPs induced by sampling subsets of the data acquired in the previous rounds. Our in-silico experiments show that meta-learning over such ensembles provides robustness against reward misspecification and achieves competitive results compared to existing strong baselines.

On the adaptation of recurrent neural networks for system identification

This paper presents a transfer learning approach which enables fast and efficient adaptation of Recurrent Neural Network (RNN) models of dynamical systems. A nominal RNN model is first identified using available measurements. The system dynamics are then assumed to change, leading to an unacceptable degradation of the nominal model performance on the perturbed system. To cope with the mismatch, the model is augmented with an additive correction term trained on fresh data from the new dynamic regime. The correction term is learned through a Jacobian Feature Regression (JFR) method defined in terms of the features spanned by the model's Jacobian with respect to its nominal parameters. A non-parametric view of the approach is also proposed, which extends recent work on Gaussian Process (GP) with Neural Tangent Kernel (NTK-GP) to the RNN case (RNTK-GP). This can be more efficient for very large networks or when only few data points are available. Implementation aspects for fast and efficient computation of the correction term, as well as the initial state estimation for the RNN model are described. Numerical examples show the effectiveness of the proposed methodology in presence of significant system variations.