SPIKANs: Separable Physics-Informed Kolmogorov-Arnold Networks

Physics-Informed Neural Networks (PINNs) have emerged as a promising method for solving partial differential equations (PDEs) in scientific computing. While PINNs typically use multilayer perceptrons (MLPs) as their underlying architecture, recent advancements have explored alternative neural network structures. One such innovation is the Kolmogorov-Arnold Network (KAN), which has demonstrated benefits over traditional MLPs, including faster neural scaling and better interpretability. The application of KANs to physics-informed learning has led to the development of Physics-Informed KANs (PIKANs), enabling the use of KANs to solve PDEs. However, despite their advantages, KANs often suffer from slower training speeds, particularly in higher-dimensional problems where the number of collocation points grows exponentially with the dimensionality of the system. To address this challenge, we introduce Separable Physics-Informed Kolmogorov-Arnold Networks (SPIKANs). This novel architecture applies the principle of separation of variables to PIKANs, decomposing the problem such that each dimension is handled by an individual KAN. This approach drastically reduces the computational complexity of training without sacrificing accuracy, facilitating their application to higher-dimensional PDEs. Through a series of benchmark problems, we demonstrate the effectiveness of SPIKANs, showcasing their superior scalability and performance compared to PIKANs and highlighting their potential for solving complex, high-dimensional PDEs in scientific computing.

Multifidelity Kolmogorov-Arnold Networks

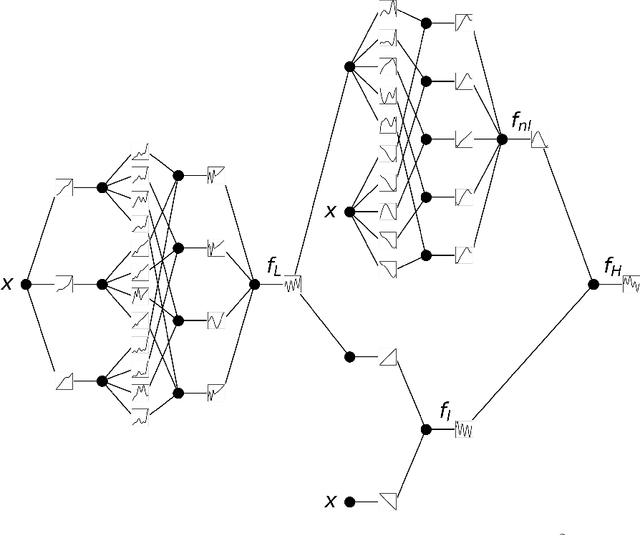
We develop a method for multifidelity Kolmogorov-Arnold networks (KANs), which use a low-fidelity model along with a small amount of high-fidelity data to train a model for the high-fidelity data accurately. Multifidelity KANs (MFKANs) reduce the amount of expensive high-fidelity data needed to accurately train a KAN by exploiting the correlations between the low- and high-fidelity data to give accurate and robust predictions in the absence of a large high-fidelity dataset. In addition, we show that multifidelity KANs can be used to increase the accuracy of physics-informed KANs (PIKANs), without the use of training data.

Finite basis Kolmogorov-Arnold networks: domain decomposition for data-driven and physics-informed problems

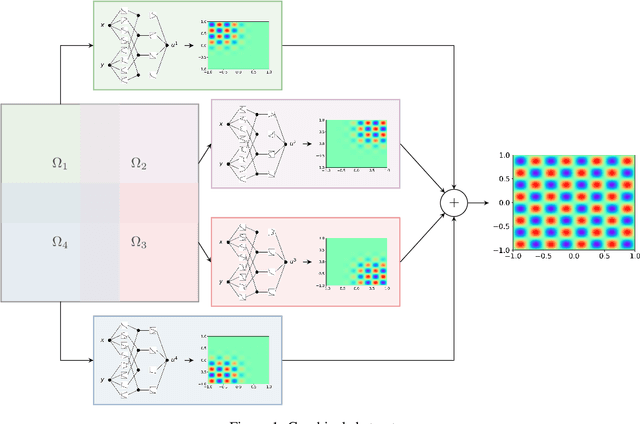
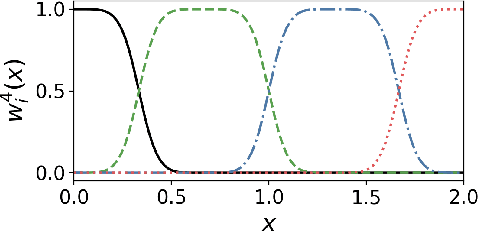
Kolmogorov-Arnold networks (KANs) have attracted attention recently as an alternative to multilayer perceptrons (MLPs) for scientific machine learning. However, KANs can be expensive to train, even for relatively small networks. Inspired by finite basis physics-informed neural networks (FBPINNs), in this work, we develop a domain decomposition method for KANs that allows for several small KANs to be trained in parallel to give accurate solutions for multiscale problems. We show that finite basis KANs (FBKANs) can provide accurate results with noisy data and for physics-informed training.