STARS: Sensor-agnostic Transformer Architecture for Remote Sensing

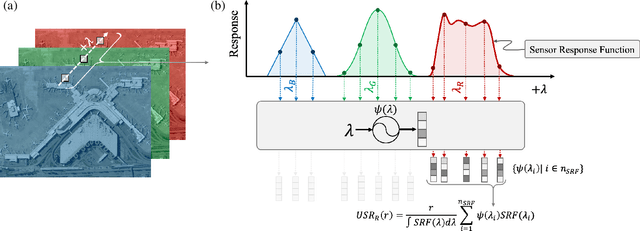
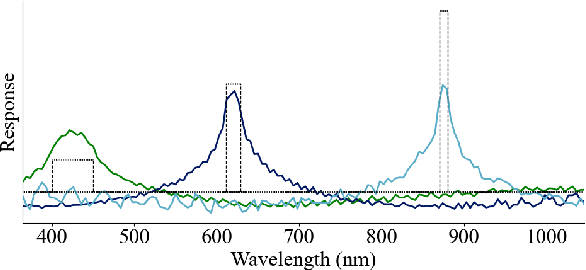
We present a sensor-agnostic spectral transformer as the basis for spectral foundation models. To that end, we introduce a Universal Spectral Representation (USR) that leverages sensor meta-data, such as sensing kernel specifications and sensing wavelengths, to encode spectra obtained from any spectral instrument into a common representation, such that a single model can ingest data from any sensor. Furthermore, we develop a methodology for pre-training such models in a self-supervised manner using a novel random sensor-augmentation and reconstruction pipeline to learn spectral features independent of the sensing paradigm. We demonstrate that our architecture can learn sensor independent spectral features that generalize effectively to sensors not seen during training. This work sets the stage for training foundation models that can both leverage and be effective for the growing diversity of spectral data.

Metric Learning to Accelerate Convergence of Operator Splitting Methods for Differentiable Parametric Programming

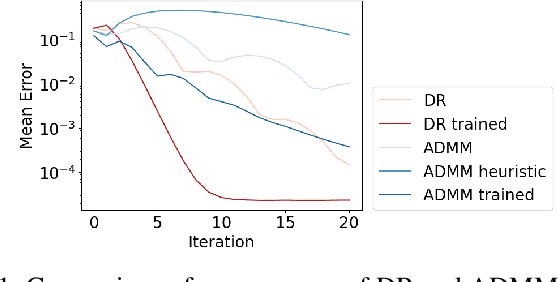
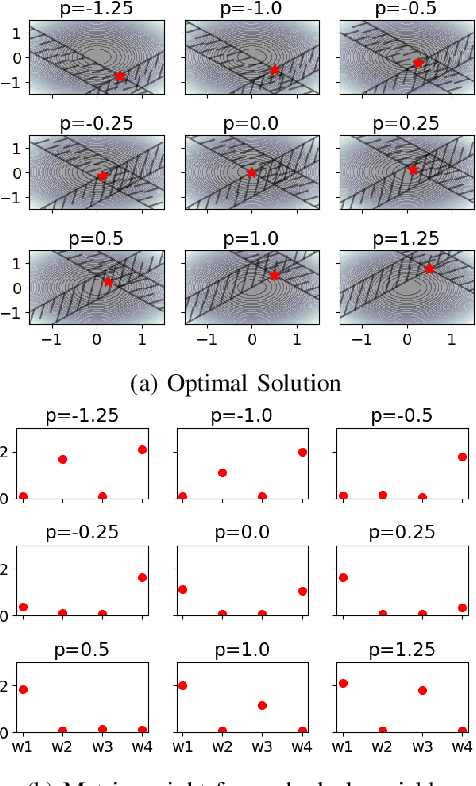
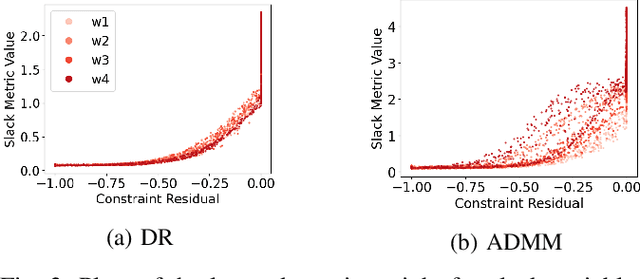
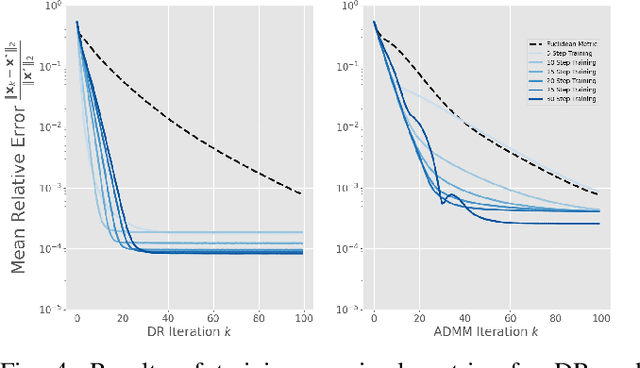
Recent work has shown a variety of ways in which machine learning can be used to accelerate the solution of constrained optimization problems. Increasing demand for real-time decision-making capabilities in applications such as artificial intelligence and optimal control has led to a variety of approaches, based on distinct strategies. This work proposes a novel approach to learning optimization, in which the underlying metric space of a proximal operator splitting algorithm is learned so as to maximize its convergence rate. While prior works in optimization theory have derived optimal metrics for limited classes of problems, the results do not extend to many practical problem forms including general Quadratic Programming (QP). This paper shows how differentiable optimization can enable the end-to-end learning of proximal metrics, enhancing the convergence of proximal algorithms for QP problems beyond what is possible based on known theory. Additionally, the results illustrate a strong connection between the learned proximal metrics and active constraints at the optima, leading to an interpretation in which the learning of proximal metrics can be viewed as a form of active set learning.

Neural Lumped Parameter Differential Equations with Application in Friction-Stir Processing

Lumped parameter methods aim to simplify the evolution of spatially-extended or continuous physical systems to that of a "lumped" element representative of the physical scales of the modeled system. For systems where the definition of a lumped element or its associated physics may be unknown, modeling tasks may be restricted to full-fidelity simulations of the physics of a system. In this work, we consider data-driven modeling tasks with limited point-wise measurements of otherwise continuous systems. We build upon the notion of the Universal Differential Equation (UDE) to construct data-driven models for reducing dynamics to that of a lumped parameter and inferring its properties. The flexibility of UDEs allow for composing various known physical priors suitable for application-specific modeling tasks, including lumped parameter methods. The motivating example for this work is the plunge and dwell stages for friction-stir welding; specifically, (i) mapping power input into the tool to a point-measurement of temperature and (ii) using this learned mapping for process control.