Keerti Kappagantula
Neural Lumped Parameter Differential Equations with Application in Friction-Stir Processing
Apr 18, 2023Abstract:Lumped parameter methods aim to simplify the evolution of spatially-extended or continuous physical systems to that of a "lumped" element representative of the physical scales of the modeled system. For systems where the definition of a lumped element or its associated physics may be unknown, modeling tasks may be restricted to full-fidelity simulations of the physics of a system. In this work, we consider data-driven modeling tasks with limited point-wise measurements of otherwise continuous systems. We build upon the notion of the Universal Differential Equation (UDE) to construct data-driven models for reducing dynamics to that of a lumped parameter and inferring its properties. The flexibility of UDEs allow for composing various known physical priors suitable for application-specific modeling tasks, including lumped parameter methods. The motivating example for this work is the plunge and dwell stages for friction-stir welding; specifically, (i) mapping power input into the tool to a point-measurement of temperature and (ii) using this learned mapping for process control.
Fiber Bundle Morphisms as a Framework for Modeling Many-to-Many Maps
Mar 15, 2022


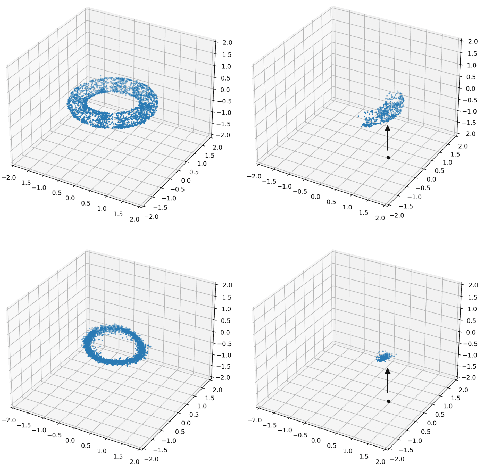
Abstract:While it is not generally reflected in the `nice' datasets used for benchmarking machine learning algorithms, the real-world is full of processes that would be best described as many-to-many. That is, a single input can potentially yield many different outputs (whether due to noise, imperfect measurement, or intrinsic stochasticity in the process) and many different inputs can yield the same output (that is, the map is not injective). For example, imagine a sentiment analysis task where, due to linguistic ambiguity, a single statement can have a range of different sentiment interpretations while at the same time many distinct statements can represent the same sentiment. When modeling such a multivalued function $f: X \rightarrow Y$, it is frequently useful to be able to model the distribution on $f(x)$ for specific input $x$ as well as the distribution on fiber $f^{-1}(y)$ for specific output $y$. Such an analysis helps the user (i) better understand the variance intrinsic to the process they are studying and (ii) understand the range of specific input $x$ that can be used to achieve output $y$. Following existing work which used a fiber bundle framework to better model many-to-one processes, we describe how morphisms of fiber bundles provide a template for building models which naturally capture the structure of many-to-many processes.
Differential Property Prediction: A Machine Learning Approach to Experimental Design in Advanced Manufacturing
Dec 03, 2021



Abstract:Advanced manufacturing techniques have enabled the production of materials with state-of-the-art properties. In many cases however, the development of physics-based models of these techniques lags behind their use in the lab. This means that designing and running experiments proceeds largely via trial and error. This is sub-optimal since experiments are cost-, time-, and labor-intensive. In this work we propose a machine learning framework, differential property classification (DPC), which enables an experimenter to leverage machine learning's unparalleled pattern matching capability to pursue data-driven experimental design. DPC takes two possible experiment parameter sets and outputs a prediction of which will produce a material with a more desirable property specified by the operator. We demonstrate the success of DPC on AA7075 tube manufacturing process and mechanical property data using shear assisted processing and extrusion (ShAPE), a solid phase processing technology. We show that by focusing on the experimenter's need to choose between multiple candidate experimental parameters, we can reframe the challenging regression task of predicting material properties from processing parameters, into a classification task on which machine learning models can achieve good performance.
A Topological-Framework to Improve Analysis of Machine Learning Model Performance
Jul 09, 2021

Abstract:As both machine learning models and the datasets on which they are evaluated have grown in size and complexity, the practice of using a few summary statistics to understand model performance has become increasingly problematic. This is particularly true in real-world scenarios where understanding model failure on certain subpopulations of the data is of critical importance. In this paper we propose a topological framework for evaluating machine learning models in which a dataset is treated as a "space" on which a model operates. This provides us with a principled way to organize information about model performance at both the global level (over the entire test set) and also the local level (on specific subpopulations). Finally, we describe a topological data structure, presheaves, which offer a convenient way to store and analyze model performance between different subpopulations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge