Colby Wight
Fiber Bundle Morphisms as a Framework for Modeling Many-to-Many Maps
Mar 15, 2022


Abstract:While it is not generally reflected in the `nice' datasets used for benchmarking machine learning algorithms, the real-world is full of processes that would be best described as many-to-many. That is, a single input can potentially yield many different outputs (whether due to noise, imperfect measurement, or intrinsic stochasticity in the process) and many different inputs can yield the same output (that is, the map is not injective). For example, imagine a sentiment analysis task where, due to linguistic ambiguity, a single statement can have a range of different sentiment interpretations while at the same time many distinct statements can represent the same sentiment. When modeling such a multivalued function $f: X \rightarrow Y$, it is frequently useful to be able to model the distribution on $f(x)$ for specific input $x$ as well as the distribution on fiber $f^{-1}(y)$ for specific output $y$. Such an analysis helps the user (i) better understand the variance intrinsic to the process they are studying and (ii) understand the range of specific input $x$ that can be used to achieve output $y$. Following existing work which used a fiber bundle framework to better model many-to-one processes, we describe how morphisms of fiber bundles provide a template for building models which naturally capture the structure of many-to-many processes.
Differential Property Prediction: A Machine Learning Approach to Experimental Design in Advanced Manufacturing
Dec 03, 2021



Abstract:Advanced manufacturing techniques have enabled the production of materials with state-of-the-art properties. In many cases however, the development of physics-based models of these techniques lags behind their use in the lab. This means that designing and running experiments proceeds largely via trial and error. This is sub-optimal since experiments are cost-, time-, and labor-intensive. In this work we propose a machine learning framework, differential property classification (DPC), which enables an experimenter to leverage machine learning's unparalleled pattern matching capability to pursue data-driven experimental design. DPC takes two possible experiment parameter sets and outputs a prediction of which will produce a material with a more desirable property specified by the operator. We demonstrate the success of DPC on AA7075 tube manufacturing process and mechanical property data using shear assisted processing and extrusion (ShAPE), a solid phase processing technology. We show that by focusing on the experimenter's need to choose between multiple candidate experimental parameters, we can reframe the challenging regression task of predicting material properties from processing parameters, into a classification task on which machine learning models can achieve good performance.
A Topological-Framework to Improve Analysis of Machine Learning Model Performance
Jul 09, 2021

Abstract:As both machine learning models and the datasets on which they are evaluated have grown in size and complexity, the practice of using a few summary statistics to understand model performance has become increasingly problematic. This is particularly true in real-world scenarios where understanding model failure on certain subpopulations of the data is of critical importance. In this paper we propose a topological framework for evaluating machine learning models in which a dataset is treated as a "space" on which a model operates. This provides us with a principled way to organize information about model performance at both the global level (over the entire test set) and also the local level (on specific subpopulations). Finally, we describe a topological data structure, presheaves, which offer a convenient way to store and analyze model performance between different subpopulations.
Constrained Block Nonlinear Neural Dynamical Models
Jan 06, 2021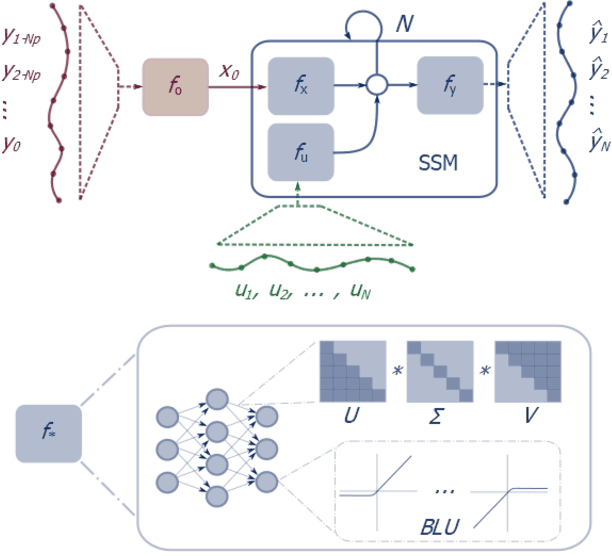


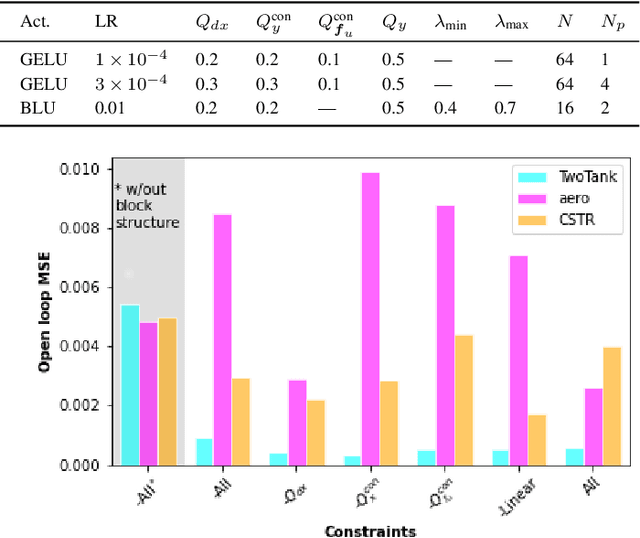
Abstract:Neural network modules conditioned by known priors can be effectively trained and combined to represent systems with nonlinear dynamics. This work explores a novel formulation for data-efficient learning of deep control-oriented nonlinear dynamical models by embedding local model structure and constraints. The proposed method consists of neural network blocks that represent input, state, and output dynamics with constraints placed on the network weights and system variables. For handling partially observable dynamical systems, we utilize a state observer neural network to estimate the states of the system's latent dynamics. We evaluate the performance of the proposed architecture and training methods on system identification tasks for three nonlinear systems: a continuous stirred tank reactor, a two tank interacting system, and an aerodynamics body. Models optimized with a few thousand system state observations accurately represent system dynamics in open loop simulation over thousands of time steps from a single set of initial conditions. Experimental results demonstrate an order of magnitude reduction in open-loop simulation mean squared error for our constrained, block-structured neural models when compared to traditional unstructured and unconstrained neural network models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge