In What Ways Are Deep Neural Networks Invariant and How Should We Measure This?

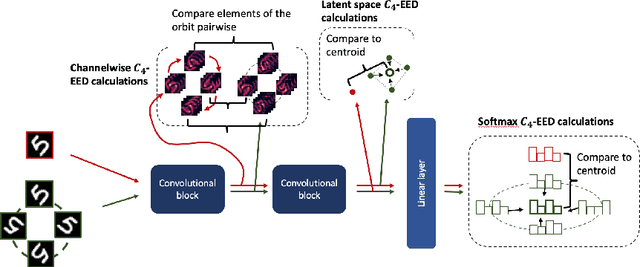
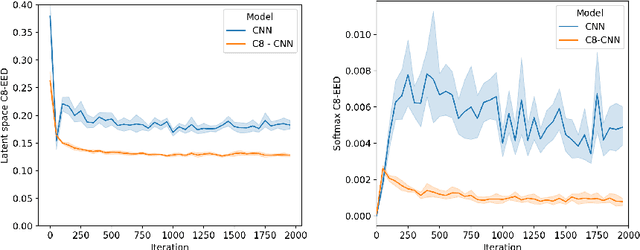
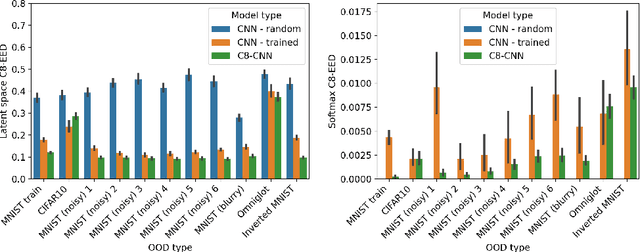
It is often said that a deep learning model is "invariant" to some specific type of transformation. However, what is meant by this statement strongly depends on the context in which it is made. In this paper we explore the nature of invariance and equivariance of deep learning models with the goal of better understanding the ways in which they actually capture these concepts on a formal level. We introduce a family of invariance and equivariance metrics that allows us to quantify these properties in a way that disentangles them from other metrics such as loss or accuracy. We use our metrics to better understand the two most popular methods used to build invariance into networks: data augmentation and equivariant layers. We draw a range of conclusions about invariance and equivariance in deep learning models, ranging from whether initializing a model with pretrained weights has an effect on a trained model's invariance, to the extent to which invariance learned via training can generalize to out-of-distribution data.

A Topological-Framework to Improve Analysis of Machine Learning Model Performance

As both machine learning models and the datasets on which they are evaluated have grown in size and complexity, the practice of using a few summary statistics to understand model performance has become increasingly problematic. This is particularly true in real-world scenarios where understanding model failure on certain subpopulations of the data is of critical importance. In this paper we propose a topological framework for evaluating machine learning models in which a dataset is treated as a "space" on which a model operates. This provides us with a principled way to organize information about model performance at both the global level (over the entire test set) and also the local level (on specific subpopulations). Finally, we describe a topological data structure, presheaves, which offer a convenient way to store and analyze model performance between different subpopulations.