Understanding the Inner Workings of Language Models Through Representation Dissimilarity

As language models are applied to an increasing number of real-world applications, understanding their inner workings has become an important issue in model trust, interpretability, and transparency. In this work we show that representation dissimilarity measures, which are functions that measure the extent to which two model's internal representations differ, can be a valuable tool for gaining insight into the mechanics of language models. Among our insights are: (i) an apparent asymmetry in the internal representations of model using SoLU and GeLU activation functions, (ii) evidence that dissimilarity measures can identify and locate generalization properties of models that are invisible via in-distribution test set performance, and (iii) new evaluations of how language model features vary as width and depth are increased. Our results suggest that dissimilarity measures are a promising set of tools for shedding light on the inner workings of language models.

Attributing Learned Concepts in Neural Networks to Training Data

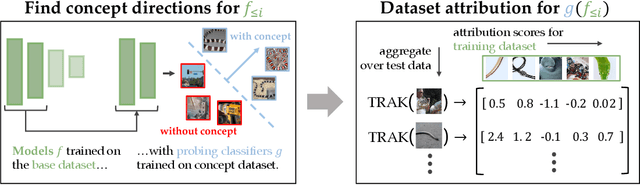
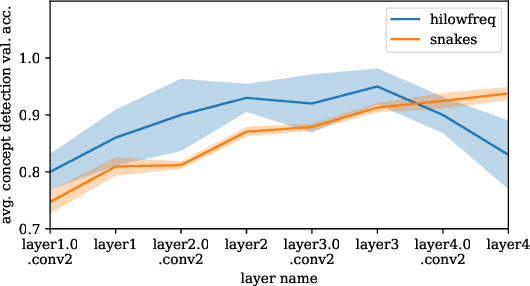
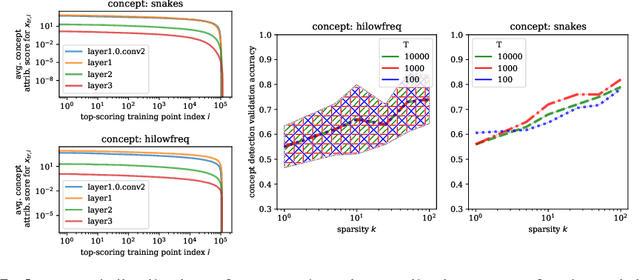
By now there is substantial evidence that deep learning models learn certain human-interpretable features as part of their internal representations of data. As having the right (or wrong) concepts is critical to trustworthy machine learning systems, it is natural to ask which inputs from the model's original training set were most important for learning a concept at a given layer. To answer this, we combine data attribution methods with methods for probing the concepts learned by a model. Training network and probe ensembles for two concept datasets on a range of network layers, we use the recently developed TRAK method for large-scale data attribution. We find some evidence for convergence, where removing the 10,000 top attributing images for a concept and retraining the model does not change the location of the concept in the network nor the probing sparsity of the concept. This suggests that rather than being highly dependent on a few specific examples, the features that inform the development of a concept are spread in a more diffuse manner across its exemplars, implying robustness in concept formation.

Impact of architecture on robustness and interpretability of multispectral deep neural networks

Including information from additional spectral bands (e.g., near-infrared) can improve deep learning model performance for many vision-oriented tasks. There are many possible ways to incorporate this additional information into a deep learning model, but the optimal fusion strategy has not yet been determined and can vary between applications. At one extreme, known as "early fusion," additional bands are stacked as extra channels to obtain an input image with more than three channels. At the other extreme, known as "late fusion," RGB and non-RGB bands are passed through separate branches of a deep learning model and merged immediately before a final classification or segmentation layer. In this work, we characterize the performance of a suite of multispectral deep learning models with different fusion approaches, quantify their relative reliance on different input bands and evaluate their robustness to naturalistic image corruptions affecting one or more input channels.

Neural Image Compression: Generalization, Robustness, and Spectral Biases

Recent neural image compression (NIC) advances have produced models which are starting to outperform traditional codecs. While this has led to growing excitement about using NIC in real-world applications, the successful adoption of any machine learning system in the wild requires it to generalize (and be robust) to unseen distribution shifts at deployment. Unfortunately, current research lacks comprehensive datasets and informative tools to evaluate and understand NIC performance in real-world settings. To bridge this crucial gap, first, this paper presents a comprehensive benchmark suite to evaluate the out-of-distribution (OOD) performance of image compression methods. Specifically, we provide CLIC-C and Kodak-C by introducing 15 corruptions to popular CLIC and Kodak benchmarks. Next, we propose spectrally inspired inspection tools to gain deeper insight into errors introduced by image compression methods as well as their OOD performance. We then carry out a detailed performance comparison of a classical codec with several NIC variants, revealing intriguing findings that challenge our current understanding of the strengths and limitations of NIC. Finally, we corroborate our empirical findings with theoretical analysis, providing an in-depth view of the OOD performance of NIC and its dependence on the spectral properties of the data. Our benchmarks, spectral inspection tools, and findings provide a crucial bridge to the real-world adoption of NIC. We hope that our work will propel future efforts in designing robust and generalizable NIC methods. Code and data will be made available at https://github.com/klieberman/ood_nic.

Quantifying the robustness of deep multispectral segmentation models against natural perturbations and data poisoning

In overhead image segmentation tasks, including additional spectral bands beyond the traditional RGB channels can improve model performance. However, it is still unclear how incorporating this additional data impacts model robustness to adversarial attacks and natural perturbations. For adversarial robustness, the additional information could improve the model's ability to distinguish malicious inputs, or simply provide new attack avenues and vulnerabilities. For natural perturbations, the additional information could better inform model decisions and weaken perturbation effects or have no significant influence at all. In this work, we seek to characterize the performance and robustness of a multispectral (RGB and near infrared) image segmentation model subjected to adversarial attacks and natural perturbations. While existing adversarial and natural robustness research has focused primarily on digital perturbations, we prioritize on creating realistic perturbations designed with physical world conditions in mind. For adversarial robustness, we focus on data poisoning attacks whereas for natural robustness, we focus on extending ImageNet-C common corruptions for fog and snow that coherently and self-consistently perturbs the input data. Overall, we find both RGB and multispectral models are vulnerable to data poisoning attacks regardless of input or fusion architectures and that while physically realizable natural perturbations still degrade model performance, the impact differs based on fusion architecture and input data.

How many dimensions are required to find an adversarial example?

Past work exploring adversarial vulnerability have focused on situations where an adversary can perturb all dimensions of model input. On the other hand, a range of recent works consider the case where either (i) an adversary can perturb a limited number of input parameters or (ii) a subset of modalities in a multimodal problem. In both of these cases, adversarial examples are effectively constrained to a subspace $V$ in the ambient input space $\mathcal{X}$. Motivated by this, in this work we investigate how adversarial vulnerability depends on $\dim(V)$. In particular, we show that the adversarial success of standard PGD attacks with $\ell^p$ norm constraints behaves like a monotonically increasing function of $\epsilon (\frac{\dim(V)}{\dim \mathcal{X}})^{\frac{1}{q}}$ where $\epsilon$ is the perturbation budget and $\frac{1}{p} + \frac{1}{q} =1$, provided $p > 1$ (the case $p=1$ presents additional subtleties which we analyze in some detail). This functional form can be easily derived from a simple toy linear model, and as such our results land further credence to arguments that adversarial examples are endemic to locally linear models on high dimensional spaces.

Fast computation of permutation equivariant layers with the partition algebra

Linear neural network layers that are either equivariant or invariant to permutations of their inputs form core building blocks of modern deep learning architectures. Examples include the layers of DeepSets, as well as linear layers occurring in attention blocks of transformers and some graph neural networks. The space of permutation equivariant linear layers can be identified as the invariant subspace of a certain symmetric group representation, and recent work parameterized this space by exhibiting a basis whose vectors are sums over orbits of standard basis elements with respect to the symmetric group action. A parameterization opens up the possibility of learning the weights of permutation equivariant linear layers via gradient descent. The space of permutation equivariant linear layers is a generalization of the partition algebra, an object first discovered in statistical physics with deep connections to the representation theory of the symmetric group, and the basis described above generalizes the so-called orbit basis of the partition algebra. We exhibit an alternative basis, generalizing the diagram basis of the partition algebra, with computational benefits stemming from the fact that the tensors making up the basis are low rank in the sense that they naturally factorize into Kronecker products. Just as multiplication by a rank one matrix is far less expensive than multiplication by an arbitrary matrix, multiplication with these low rank tensors is far less expensive than multiplication with elements of the orbit basis. Finally, we describe an algorithm implementing multiplication with these basis elements.

Robustness of edited neural networks

Successful deployment in uncertain, real-world environments requires that deep learning models can be efficiently and reliably modified in order to adapt to unexpected issues. However, the current trend toward ever-larger models makes standard retraining procedures an ever-more expensive burden. For this reason, there is growing interest in model editing, which enables computationally inexpensive, interpretable, post-hoc model modifications. While many model editing techniques are promising, research on the properties of edited models is largely limited to evaluation of validation accuracy. The robustness of edited models is an important and yet mostly unexplored topic. In this paper, we employ recently developed techniques from the field of deep learning robustness to investigate both how model editing affects the general robustness of a model, as well as the robustness of the specific behavior targeted by the edit. We find that edits tend to reduce general robustness, but that the degree of degradation depends on the editing algorithm chosen. In particular, robustness is best preserved by more constrained techniques that modify less of the model. Motivated by these observations, we introduce two new model editing algorithms, direct low-rank model editing and 1-layer interpolation (1-LI), which each exhibit strong generalization performance.

Exploring the Representation Manifolds of Stable Diffusion Through the Lens of Intrinsic Dimension

Prompting has become an important mechanism by which users can more effectively interact with many flavors of foundation model. Indeed, the last several years have shown that well-honed prompts can sometimes unlock emergent capabilities within such models. While there has been a substantial amount of empirical exploration of prompting within the community, relatively few works have studied prompting at a mathematical level. In this work we aim to take a first step towards understanding basic geometric properties induced by prompts in Stable Diffusion, focusing on the intrinsic dimension of internal representations within the model. We find that choice of prompt has a substantial impact on the intrinsic dimension of representations at both layers of the model which we explored, but that the nature of this impact depends on the layer being considered. For example, in certain bottleneck layers of the model, intrinsic dimension of representations is correlated with prompt perplexity (measured using a surrogate model), while this correlation is not apparent in the latent layers. Our evidence suggests that intrinsic dimension could be a useful tool for future studies of the impact of different prompts on text-to-image models.

Neural frames: A Tool for Studying the Tangent Bundles Underlying Image Datasets and How Deep Learning Models Process Them

The assumption that many forms of high-dimensional data, such as images, actually live on low-dimensional manifolds, sometimes known as the manifold hypothesis, underlies much of our intuition for how and why deep learning works. Despite the central role that they play in our intuition, data manifolds are surprisingly hard to measure in the case of high-dimensional, sparsely sampled image datasets. This is particularly frustrating since the capability to measure data manifolds would provide a revealing window into the inner workings and dynamics of deep learning models. Motivated by this, we introduce neural frames, a novel and easy to use tool inspired by the notion of a frame from differential geometry. Neural frames can be used to explore the local neighborhoods of data manifolds as they pass through the hidden layers of neural networks even when one only has a single datapoint available. We present a mathematical framework for neural frames and explore some of their properties. We then use them to make a range of observations about how modern model architectures and training routines, such as heavy augmentation and adversarial training, affect the local behavior of a model.