Reproducing Kernel Hilbert Space Pruning for Sparse Hyperspectral Abundance Prediction

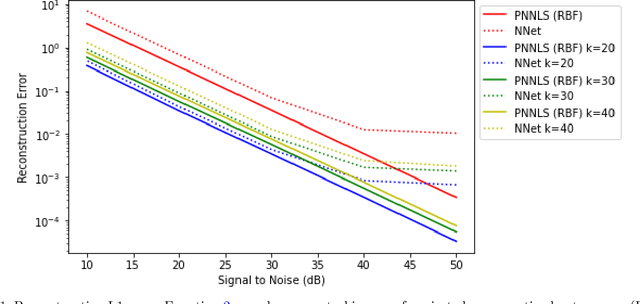
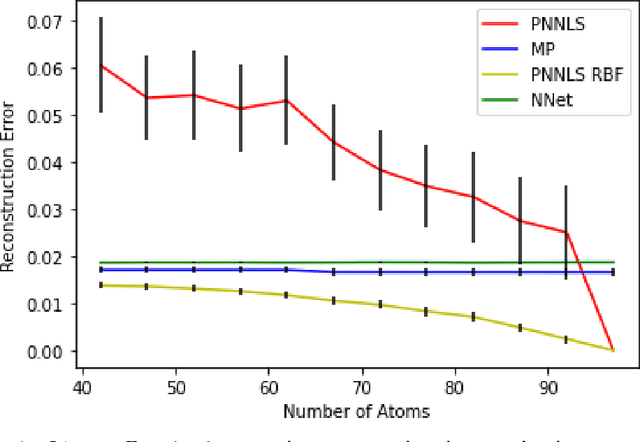
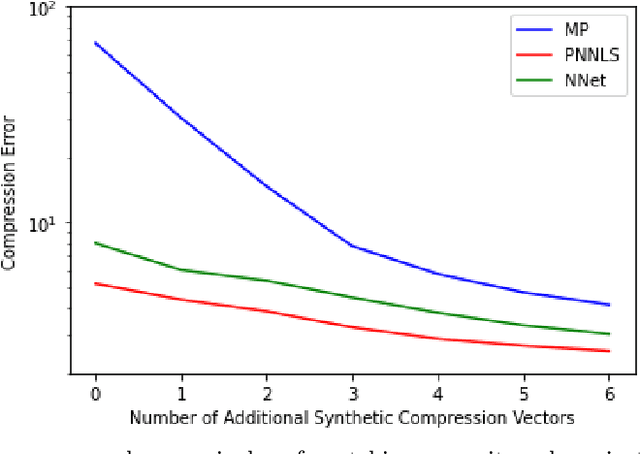
Hyperspectral measurements from long range sensors can give a detailed picture of the items, materials, and chemicals in a scene but analysis can be difficult, slow, and expensive due to high spatial and spectral resolutions of state-of-the-art sensors. As such, sparsity is important to enable the future of spectral compression and analytics. It has been observed that environmental and atmospheric effects, including scattering, can produce nonlinear effects posing challenges for existing source separation and compression methods. We present a novel transformation into Hilbert spaces for pruning and constructing sparse representations via non-negative least squares minimization. Then we introduce max likelihood compression vectors to decrease information loss. Our approach is benchmarked against standard pruning and least squares as well as deep learning methods. Our methods are evaluated in terms of overall spectral reconstruction error and compression rate using real and synthetic data. We find that pruning least squares methods converge quickly unlike matching pursuit methods. We find that Hilbert space pruning can reduce error by as much as 40% of the error of standard pruning and also outperform neural network autoencoders.

Fast computation of permutation equivariant layers with the partition algebra

Linear neural network layers that are either equivariant or invariant to permutations of their inputs form core building blocks of modern deep learning architectures. Examples include the layers of DeepSets, as well as linear layers occurring in attention blocks of transformers and some graph neural networks. The space of permutation equivariant linear layers can be identified as the invariant subspace of a certain symmetric group representation, and recent work parameterized this space by exhibiting a basis whose vectors are sums over orbits of standard basis elements with respect to the symmetric group action. A parameterization opens up the possibility of learning the weights of permutation equivariant linear layers via gradient descent. The space of permutation equivariant linear layers is a generalization of the partition algebra, an object first discovered in statistical physics with deep connections to the representation theory of the symmetric group, and the basis described above generalizes the so-called orbit basis of the partition algebra. We exhibit an alternative basis, generalizing the diagram basis of the partition algebra, with computational benefits stemming from the fact that the tensors making up the basis are low rank in the sense that they naturally factorize into Kronecker products. Just as multiplication by a rank one matrix is far less expensive than multiplication by an arbitrary matrix, multiplication with these low rank tensors is far less expensive than multiplication with elements of the orbit basis. Finally, we describe an algorithm implementing multiplication with these basis elements.

Renormalized Sparse Neural Network Pruning

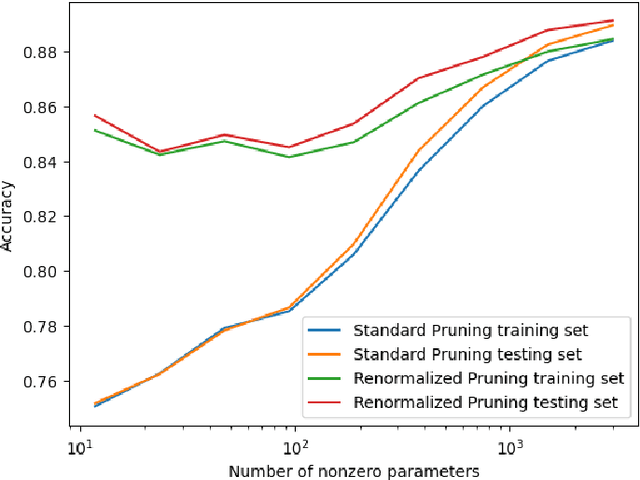
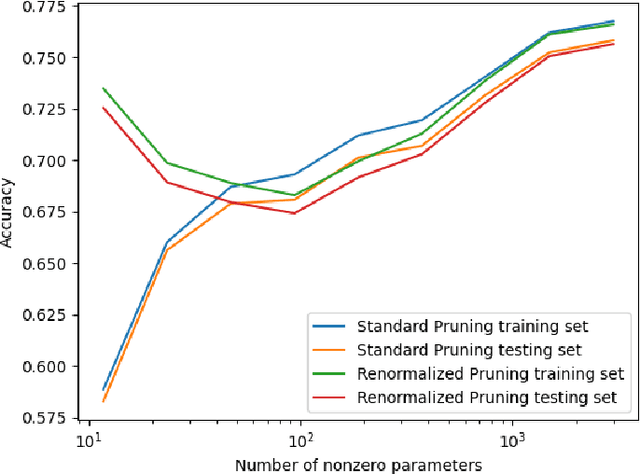
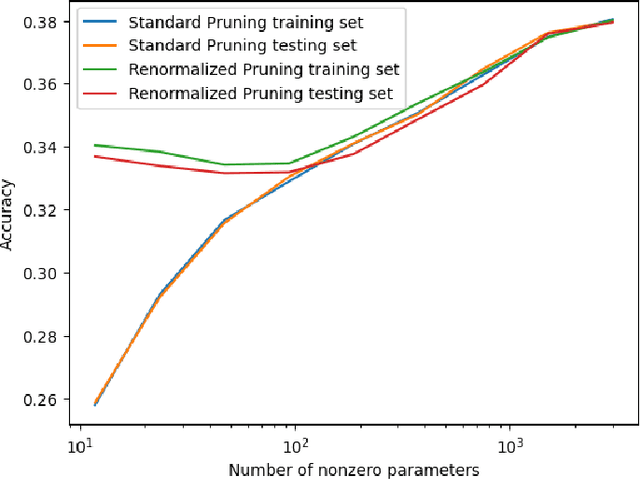
Large neural networks are heavily over-parameterized. This is done because it improves training to optimality. However once the network is trained, this means many parameters can be zeroed, or pruned, leaving an equivalent sparse neural network. We propose renormalizing sparse neural networks in order to improve accuracy. We prove that our method's error converges to 0 as network parameters cluster or concentrate. We prove that without renormalizing, the error does not converge to zero in general. We experiment with our method on real world datasets MNIST, Fashion MNIST, and CIFAR-10 and confirm a large improvement in accuracy with renormalization versus standard pruning.