Neural Differential Algebraic Equations
Paper and Code
Mar 19, 2024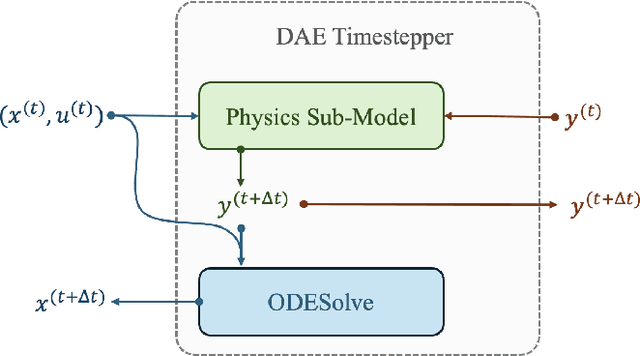
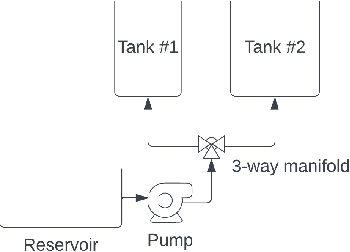
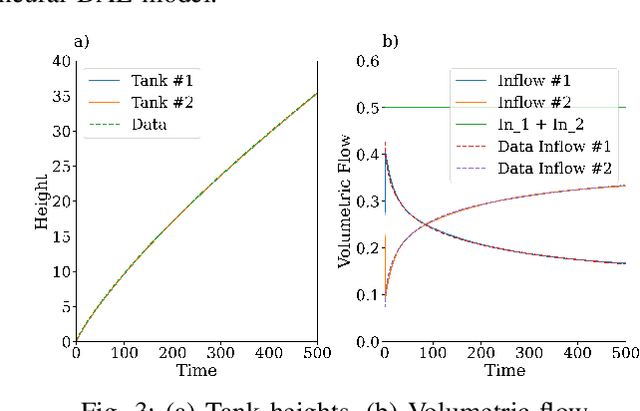
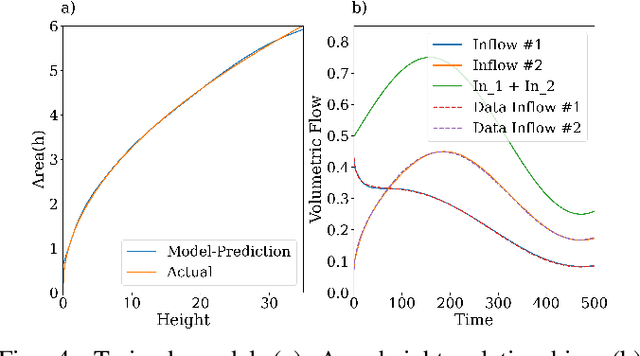
Differential-Algebraic Equations (DAEs) describe the temporal evolution of systems that obey both differential and algebraic constraints. Of particular interest are systems that contain implicit relationships between their components, such as conservation relationships. Here, we present Neural Differential-Algebraic Equations (NDAEs) suitable for data-driven modeling of DAEs. This methodology is built upon the concept of the Universal Differential Equation; that is, a model constructed as a system of Neural Ordinary Differential Equations informed by theory from particular science domains. In this work, we show that the proposed NDAEs abstraction is suitable for relevant system-theoretic data-driven modeling tasks. Presented examples include (i) the inverse problem of tank-manifold dynamics and (ii) discrepancy modeling of a network of pumps, tanks, and pipes. Our experiments demonstrate the proposed method's robustness to noise and extrapolation ability to (i) learn the behaviors of the system components and their interaction physics and (ii) disambiguate between data trends and mechanistic relationships contained in the system.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge