NervePool: A Simplicial Pooling Layer

For deep learning problems on graph-structured data, pooling layers are important for down sampling, reducing computational cost, and to minimize overfitting. We define a pooling layer, NervePool, for data structured as simplicial complexes, which are generalizations of graphs that include higher-dimensional simplices beyond vertices and edges; this structure allows for greater flexibility in modeling higher-order relationships. The proposed simplicial coarsening scheme is built upon partitions of vertices, which allow us to generate hierarchical representations of simplicial complexes, collapsing information in a learned fashion. NervePool builds on the learned vertex cluster assignments and extends to coarsening of higher dimensional simplices in a deterministic fashion. While in practice, the pooling operations are computed via a series of matrix operations, the topological motivation is a set-theoretic construction based on unions of stars of simplices and the nerve complex

Do Neural Networks Trained with Topological Features Learn Different Internal Representations?

There is a growing body of work that leverages features extracted via topological data analysis to train machine learning models. While this field, sometimes known as topological machine learning (TML), has seen some notable successes, an understanding of how the process of learning from topological features differs from the process of learning from raw data is still limited. In this work, we begin to address one component of this larger issue by asking whether a model trained with topological features learns internal representations of data that are fundamentally different than those learned by a model trained with the original raw data. To quantify ``different'', we exploit two popular metrics that can be used to measure the similarity of the hidden representations of data within neural networks, neural stitching and centered kernel alignment. From these we draw a range of conclusions about how training with topological features does and does not change the representations that a model learns. Perhaps unsurprisingly, we find that structurally, the hidden representations of models trained and evaluated on topological features differ substantially compared to those trained and evaluated on the corresponding raw data. On the other hand, our experiments show that in some cases, these representations can be reconciled (at least to the degree required to solve the corresponding task) using a simple affine transformation. We conjecture that this means that neural networks trained on raw data may extract some limited topological features in the process of making predictions.

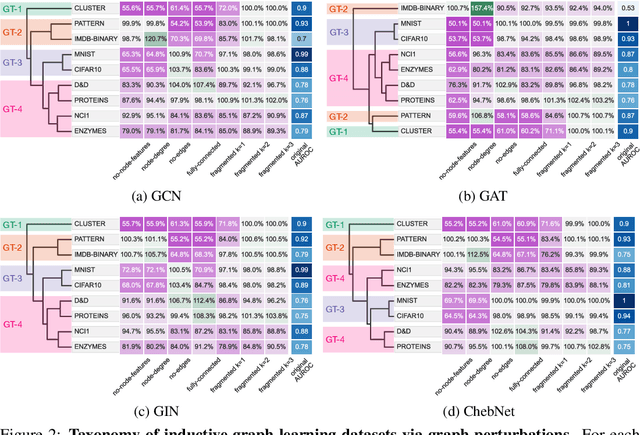
Taxonomy of Benchmarks in Graph Representation Learning

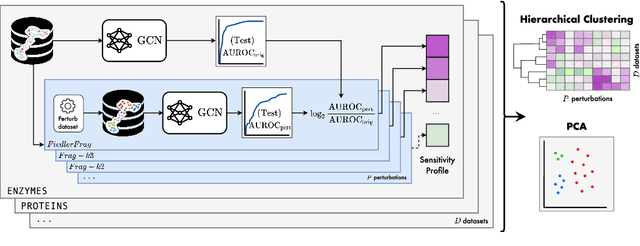
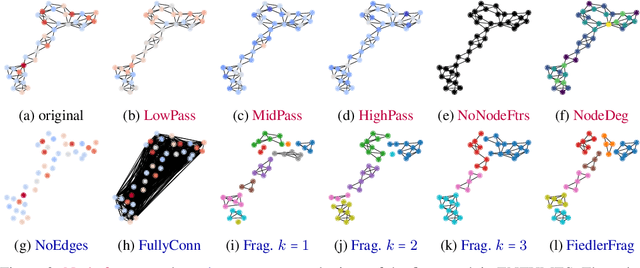
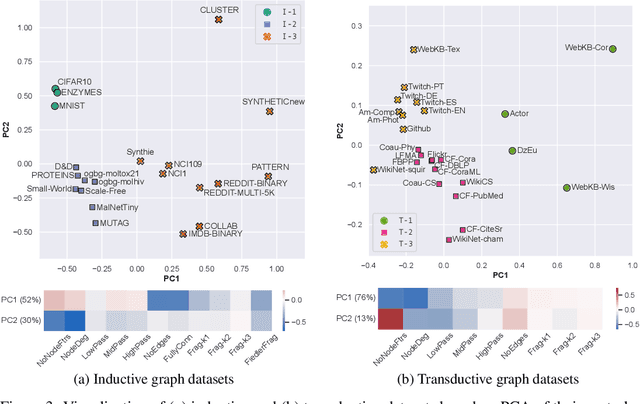
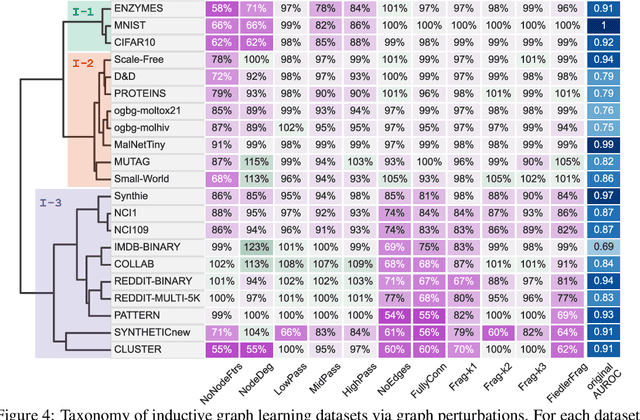
Graph Neural Networks (GNNs) extend the success of neural networks to graph-structured data by accounting for their intrinsic geometry. While extensive research has been done on developing GNN models with superior performance according to a collection of graph representation learning benchmarks, it is currently not well understood what aspects of a given model are probed by them. For example, to what extent do they test the ability of a model to leverage graph structure vs. node features? Here, we develop a principled approach to taxonomize benchmarking datasets according to a $\textit{sensitivity profile}$ that is based on how much GNN performance changes due to a collection of graph perturbations. Our data-driven analysis provides a deeper understanding of which benchmarking data characteristics are leveraged by GNNs. Consequently, our taxonomy can aid in selection and development of adequate graph benchmarks, and better informed evaluation of future GNN methods. Finally, our approach and implementation in $\texttt{GTaxoGym}$ package are extendable to multiple graph prediction task types and future datasets.

Towards a Taxonomy of Graph Learning Datasets

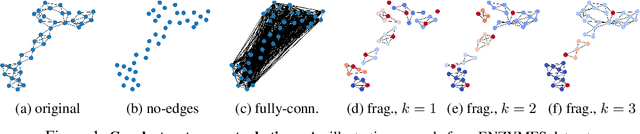
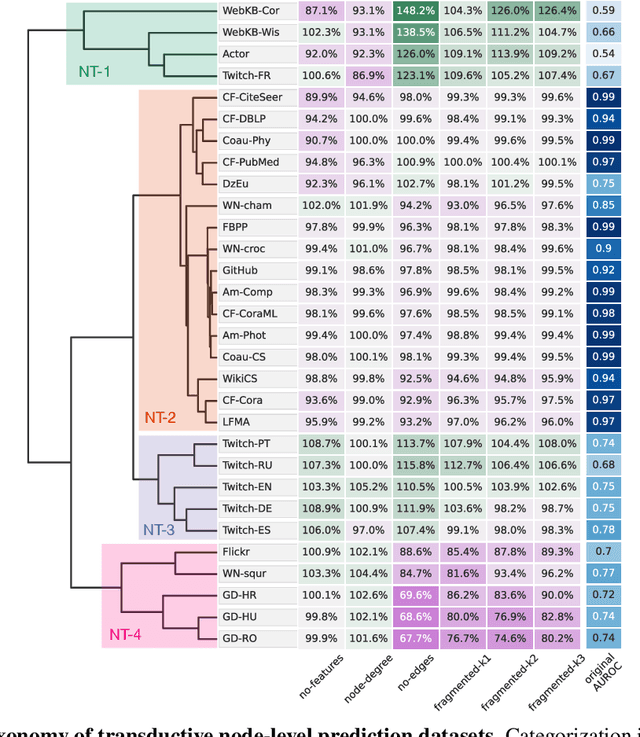
Graph neural networks (GNNs) have attracted much attention due to their ability to leverage the intrinsic geometries of the underlying data. Although many different types of GNN models have been developed, with many benchmarking procedures to demonstrate the superiority of one GNN model over the others, there is a lack of systematic understanding of the underlying benchmarking datasets, and what aspects of the model are being tested. Here, we provide a principled approach to taxonomize graph benchmarking datasets by carefully designing a collection of graph perturbations to probe the essential data characteristics that GNN models leverage to perform predictions. Our data-driven taxonomization of graph datasets provides a new understanding of critical dataset characteristics that will enable better model evaluation and the development of more specialized GNN models.