Functional Multi-Reference Alignment via Deconvolution

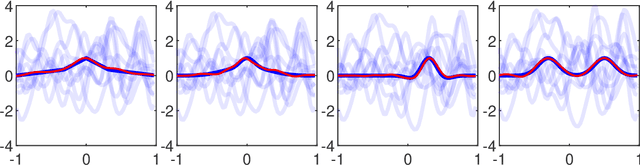
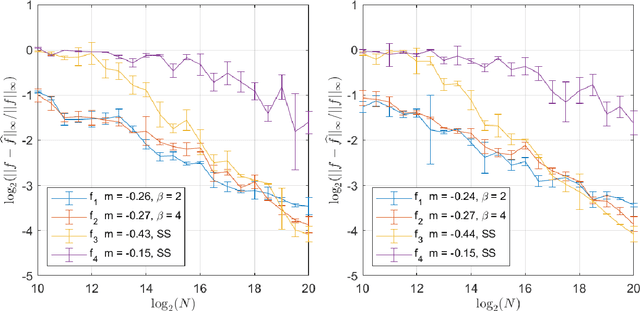
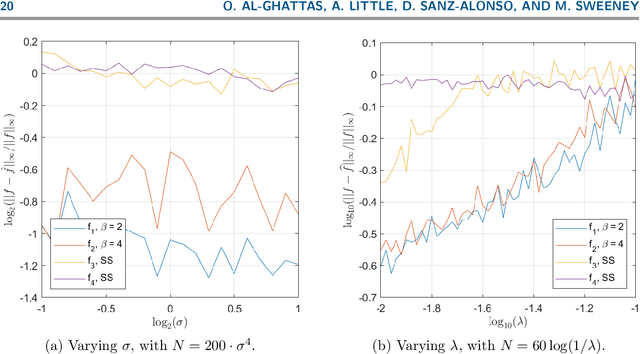
This paper studies the multi-reference alignment (MRA) problem of estimating a signal function from shifted, noisy observations. Our functional formulation reveals a new connection between MRA and deconvolution: the signal can be estimated from second-order statistics via Kotlarski's formula, an important identification result in deconvolution with replicated measurements. To design our MRA algorithms, we extend Kotlarski's formula to general dimension and study the estimation of signals with vanishing Fourier transform, thus also contributing to the deconvolution literature. We validate our deconvolution approach to MRA through both theory and numerical experiments.

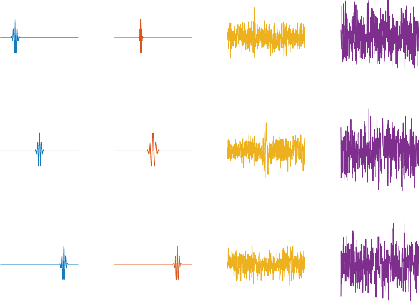
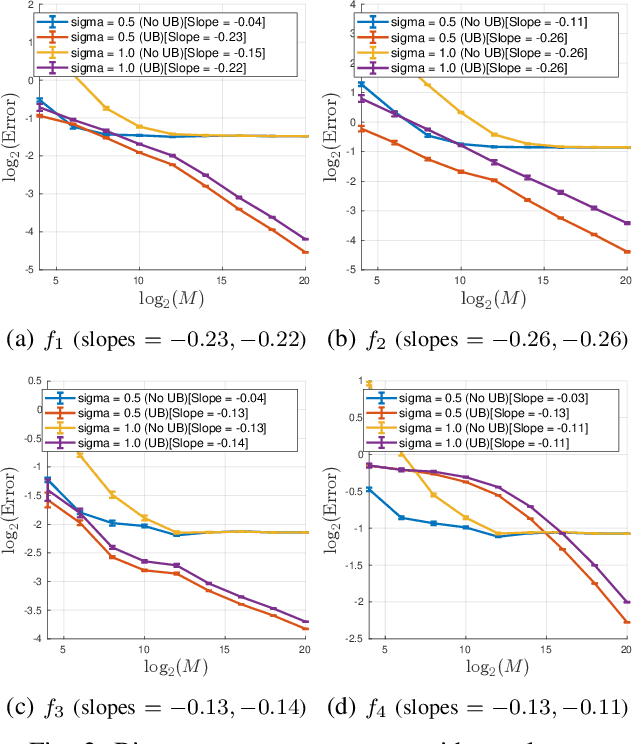
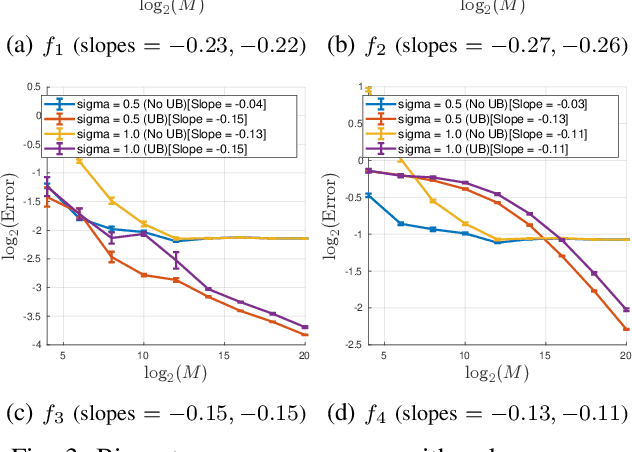
Bispectrum Unbiasing for Dilation-Invariant Multi-reference Alignment

Motivated by modern data applications such as cryo-electron microscopy, the goal of classic multi-reference alignment (MRA) is to recover an unknown signal $f: \mathbb{R} \to \mathbb{R}$ from many observations that have been randomly translated and corrupted by additive noise. We consider a generalization of classic MRA where signals are also corrupted by a random scale change, i.e. dilation. We propose a novel data-driven unbiasing procedure which can recover an unbiased estimator of the bispectrum of the unknown signal, given knowledge of the dilation distribution. Lastly, we invert the recovered bispectrum to achieve full signal recovery, and validate our methodology on a set of synthetic signals.

Fermat Distances: Metric Approximation, Spectral Convergence, and Clustering Algorithms

We analyze the convergence properties of Fermat distances, a family of density-driven metrics defined on Riemannian manifolds with an associated probability measure. Fermat distances may be defined either on discrete samples from the underlying measure, in which case they are random, or in the continuum setting, in which they are induced by geodesics under a density-distorted Riemannian metric. We prove that discrete, sample-based Fermat distances converge to their continuum analogues in small neighborhoods with a precise rate that depends on the intrinsic dimensionality of the data and the parameter governing the extent of density weighting in Fermat distances. This is done by leveraging novel geometric and statistical arguments in percolation theory that allow for non-uniform densities and curved domains. Our results are then used to prove that discrete graph Laplacians based on discrete, sample-driven Fermat distances converge to corresponding continuum operators. In particular, we show the discrete eigenvalues and eigenvectors converge to their continuum analogues at a dimension-dependent rate, which allows us to interpret the efficacy of discrete spectral clustering using Fermat distances in terms of the resulting continuum limit. The perspective afforded by our discrete-to-continuum Fermat distance analysis leads to new clustering algorithms for data and related insights into efficient computations associated to density-driven spectral clustering. Our theoretical analysis is supported with numerical simulations and experiments on synthetic and real image data.

Linear Distance Metric Learning with Noisy Labels

In linear distance metric learning, we are given data in one Euclidean metric space and the goal is to find an appropriate linear map to another Euclidean metric space which respects certain distance conditions as much as possible. In this paper, we formalize a simple and elegant method which reduces to a general continuous convex loss optimization problem, and for different noise models we derive the corresponding loss functions. We show that even if the data is noisy, the ground truth linear metric can be learned with any precision provided access to enough samples, and we provide a corresponding sample complexity bound. Moreover, we present an effective way to truncate the learned model to a low-rank model that can provably maintain the accuracy in loss function and in parameters -- the first such results of this type. Several experimental observations on synthetic and real data sets support and inform our theoretical results.

Taxonomy of Benchmarks in Graph Representation Learning

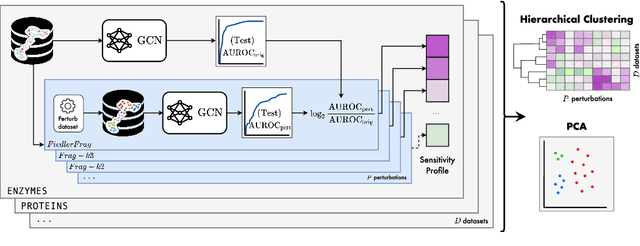
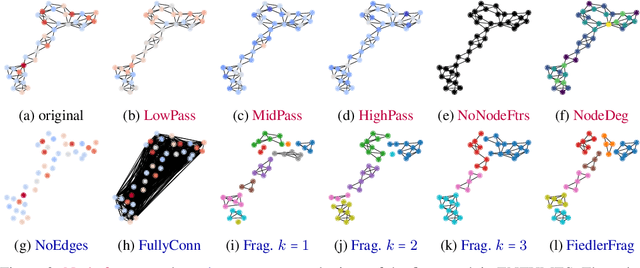
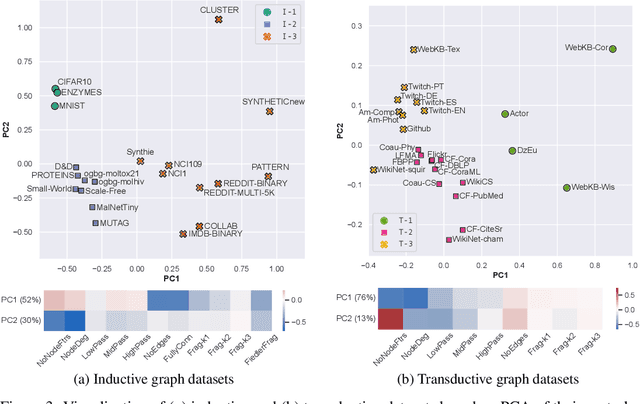
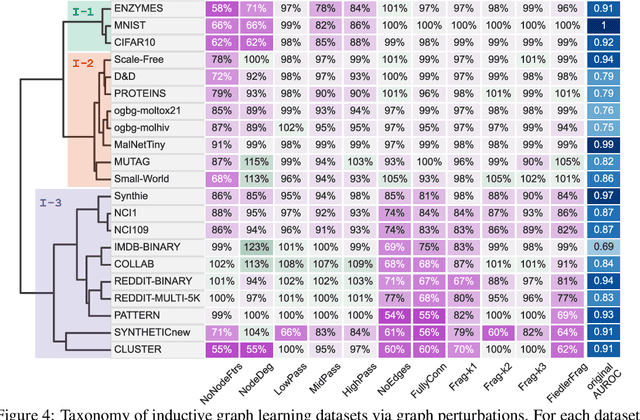
Graph Neural Networks (GNNs) extend the success of neural networks to graph-structured data by accounting for their intrinsic geometry. While extensive research has been done on developing GNN models with superior performance according to a collection of graph representation learning benchmarks, it is currently not well understood what aspects of a given model are probed by them. For example, to what extent do they test the ability of a model to leverage graph structure vs. node features? Here, we develop a principled approach to taxonomize benchmarking datasets according to a $\textit{sensitivity profile}$ that is based on how much GNN performance changes due to a collection of graph perturbations. Our data-driven analysis provides a deeper understanding of which benchmarking data characteristics are leveraged by GNNs. Consequently, our taxonomy can aid in selection and development of adequate graph benchmarks, and better informed evaluation of future GNN methods. Finally, our approach and implementation in $\texttt{GTaxoGym}$ package are extendable to multiple graph prediction task types and future datasets.

Towards a Taxonomy of Graph Learning Datasets

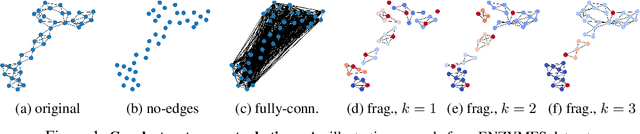
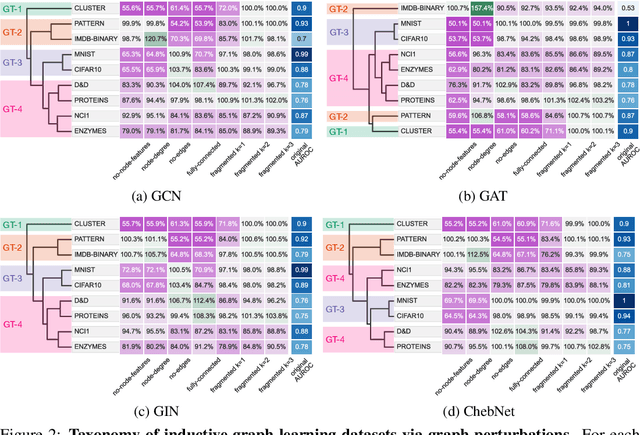
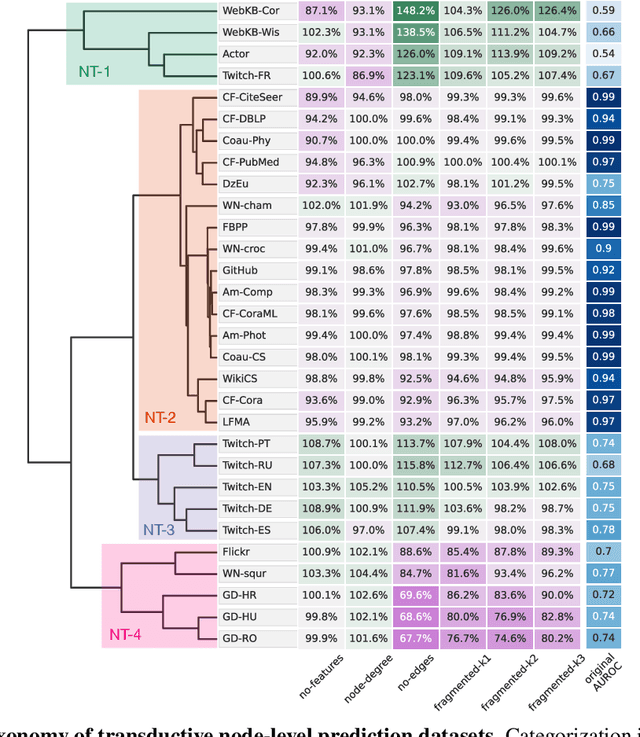
Graph neural networks (GNNs) have attracted much attention due to their ability to leverage the intrinsic geometries of the underlying data. Although many different types of GNN models have been developed, with many benchmarking procedures to demonstrate the superiority of one GNN model over the others, there is a lack of systematic understanding of the underlying benchmarking datasets, and what aspects of the model are being tested. Here, we provide a principled approach to taxonomize graph benchmarking datasets by carefully designing a collection of graph perturbations to probe the essential data characteristics that GNN models leverage to perform predictions. Our data-driven taxonomization of graph datasets provides a new understanding of critical dataset characteristics that will enable better model evaluation and the development of more specialized GNN models.

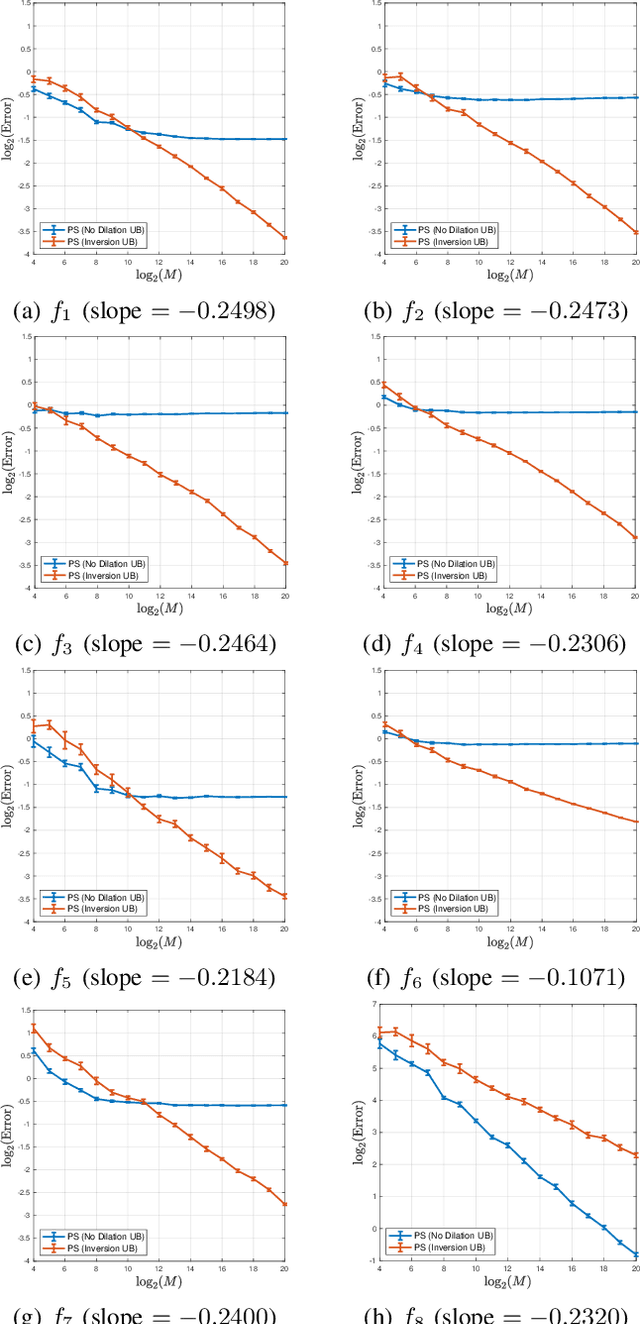
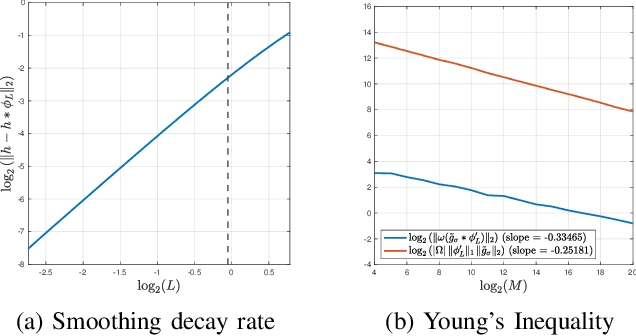
Unbiasing Procedures for Scale-invariant Multi-reference Alignment

This article discusses a generalization of the 1-dimensional multi-reference alignment problem. The goal is to recover a hidden signal from many noisy observations, where each noisy observation includes a random translation and random dilation of the hidden signal, as well as high additive noise. We propose a method that recovers the power spectrum of the hidden signal by applying a data-driven, nonlinear unbiasing procedure, and thus the hidden signal is obtained up to an unknown phase. An unbiased estimator of the power spectrum is defined, whose error depends on the sample size and noise levels, and we precisely quantify the convergence rate of the proposed estimator. The unbiasing procedure relies on knowledge of the dilation distribution, and we implement an optimization procedure to learn the dilation variance when this parameter is unknown. Our theoretical work is supported by extensive numerical experiments on a wide range of signals.

Balancing Geometry and Density: Path Distances on High-Dimensional Data

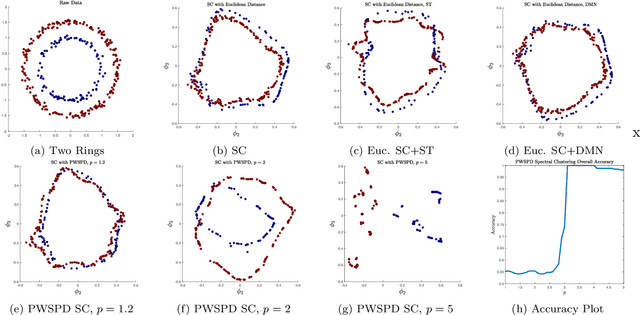
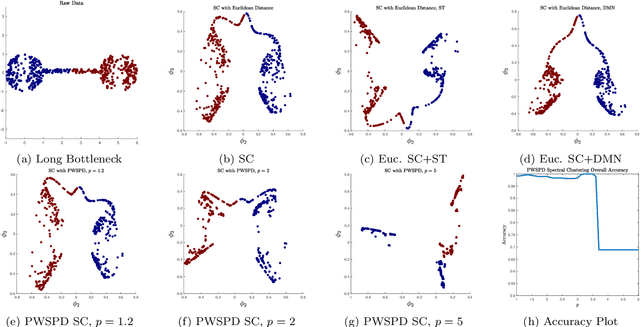
New geometric and computational analyses of power-weighted shortest-path distances (PWSPDs) are presented. By illuminating the way these metrics balance density and geometry in the underlying data, we clarify their key parameters and discuss how they may be chosen in practice. Comparisons are made with related data-driven metrics, which illustrate the broader role of density in kernel-based unsupervised and semi-supervised machine learning. Computationally, we relate PWSPDs on complete weighted graphs to their analogues on weighted nearest neighbor graphs, providing high probability guarantees on their equivalence that are near-optimal. Connections with percolation theory are developed to establish estimates on the bias and variance of PWSPDs in the finite sample setting. The theoretical results are bolstered by illustrative experiments, demonstrating the versatility of PWSPDs for a wide range of data settings. Throughout the paper, our results require only that the underlying data is sampled from a low-dimensional manifold, and depend crucially on the intrinsic dimension of this manifold, rather than its ambient dimension.

An Analysis of Classical Multidimensional Scaling

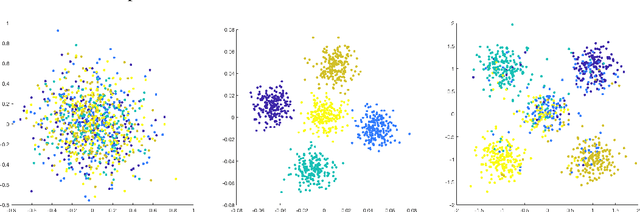
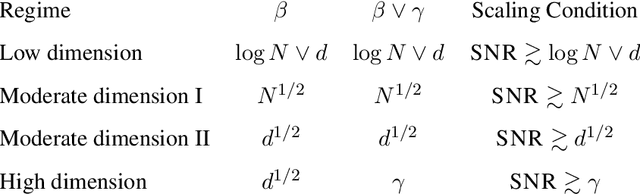
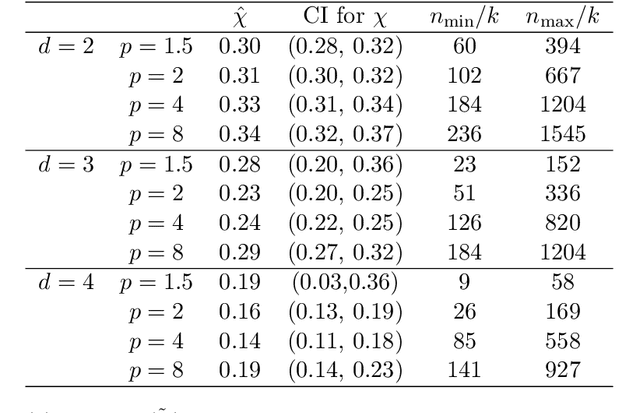
Classical multidimensional scaling is an important tool for dimension reduction in many applications. Yet few theoretical results characterizing its statistical performance exist. In this paper, we provide a theoretical framework for analyzing the quality of embedded samples produced by classical multidimensional scaling. This lays down the foundation for various downstream statistical analysis. As an application, we study its performance in the setting of clustering noisy data. Our results provide scaling conditions on the sample size, ambient dimensionality, between-class distance and noise level under which classical multidimensional scaling followed by a clustering algorithm can recover the cluster labels of all samples with high probability. Numerical simulations confirm these scaling conditions are sharp in low, moderate, and high dimensional regimes. Applications to both human RNAseq data and natural language data lend strong support to the methodology and theory.

Path-Based Spectral Clustering: Guarantees, Robustness to Outliers, and Fast Algorithms

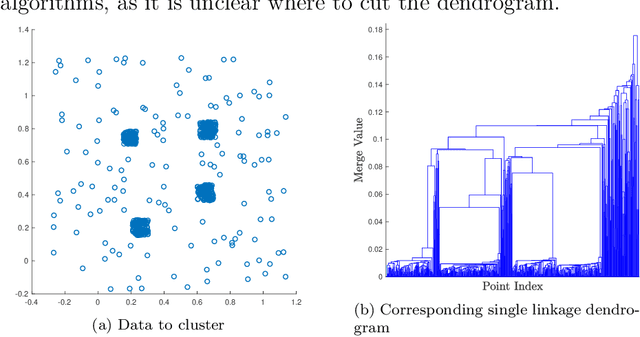
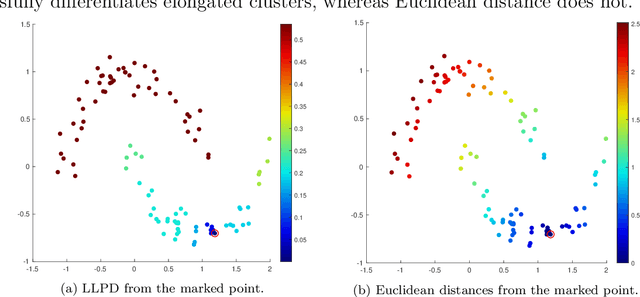
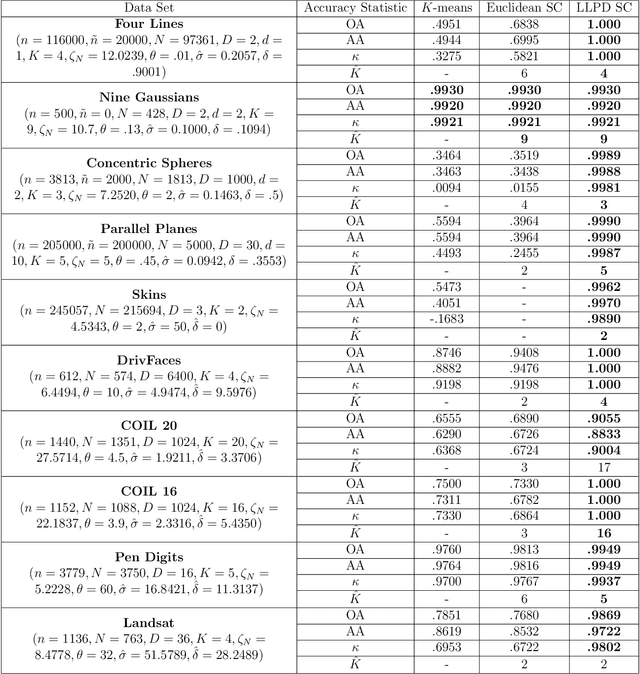
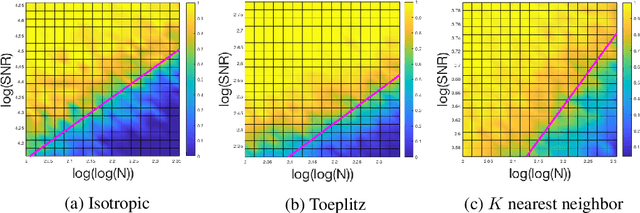
We consider the problem of clustering with the longest leg path distance (LLPD) metric, which is informative for elongated and irregularly shaped clusters. We prove finite-sample guarantees on the performance of clustering with respect to this metric when random samples are drawn from multiple intrinsically low-dimensional clusters in high-dimensional space, in the presence of a large number of high-dimensional outliers. By combining these results with spectral clustering with respect to LLPD, we provide conditions under which the eigengap statistic correctly determines the number of clusters for a large class of data sets, and prove guarantees on the number of points mislabeled by the proposed algorithm. Our methods are quite general and provide performance guarantees for spectral clustering with any ultrametric. We also introduce an efficient approximation algorithm, easy to implement, for the LLPD, based on a multiscale analysis of adjacency graphs.