An Analysis of Classical Multidimensional Scaling

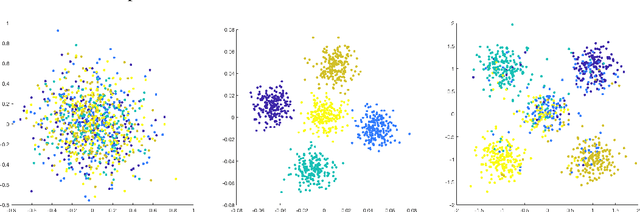
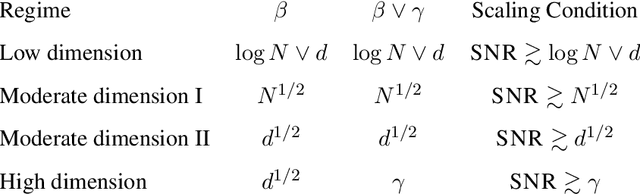
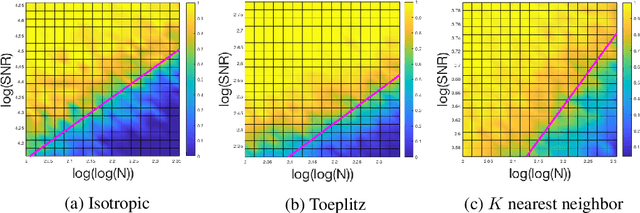
Classical multidimensional scaling is an important tool for dimension reduction in many applications. Yet few theoretical results characterizing its statistical performance exist. In this paper, we provide a theoretical framework for analyzing the quality of embedded samples produced by classical multidimensional scaling. This lays down the foundation for various downstream statistical analysis. As an application, we study its performance in the setting of clustering noisy data. Our results provide scaling conditions on the sample size, ambient dimensionality, between-class distance and noise level under which classical multidimensional scaling followed by a clustering algorithm can recover the cluster labels of all samples with high probability. Numerical simulations confirm these scaling conditions are sharp in low, moderate, and high dimensional regimes. Applications to both human RNAseq data and natural language data lend strong support to the methodology and theory.