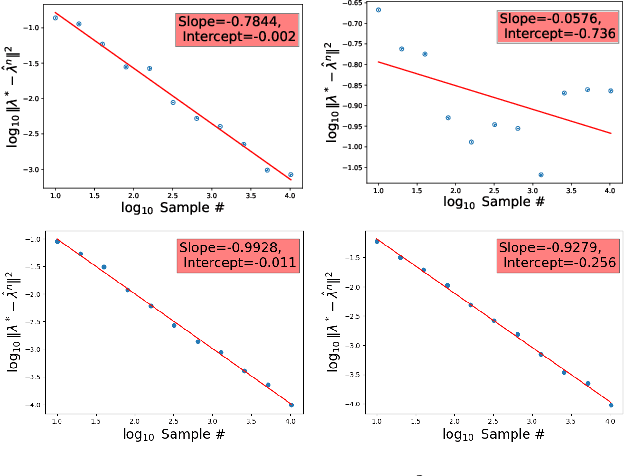
Synthesis and Analysis of Data as Probability Measures with Entropy-Regularized Optimal Transport

We consider synthesis and analysis of probability measures using the entropy-regularized Wasserstein-2 cost and its unbiased version, the Sinkhorn divergence. The synthesis problem consists of computing the barycenter, with respect to these costs, of $m$ reference measures given a set of coefficients belonging to the $m$-dimensional simplex. The analysis problem consists of finding the coefficients for the closest barycenter in the Wasserstein-2 distance to a given measure $\mu$. Under the weakest assumptions on the measures thus far in the literature, we compute the derivative of the entropy-regularized Wasserstein-2 cost. We leverage this to establish a characterization of regularized barycenters as solutions to a fixed-point equation for the average of the entropic maps from the barycenter to the reference measures. This characterization yields a finite-dimensional, convex, quadratic program for solving the analysis problem when $\mu$ is a barycenter. It is shown that these coordinates, as well as the value of the barycenter functional, can be estimated from samples with dimension-independent rates of convergence, a hallmark of entropy-regularized optimal transport, and we verify these rates experimentally. We also establish that barycentric coordinates are stable with respect to perturbations in the Wasserstein-2 metric, suggesting a robustness of these coefficients to corruptions. We employ the barycentric coefficients as features for classification of corrupted point cloud data, and show that compared to neural network baselines, our approach is more efficient in small training data regimes.

Linearized Wasserstein Barycenters: Synthesis, Analysis, Representational Capacity, and Applications

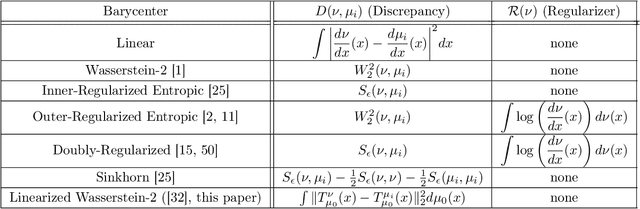
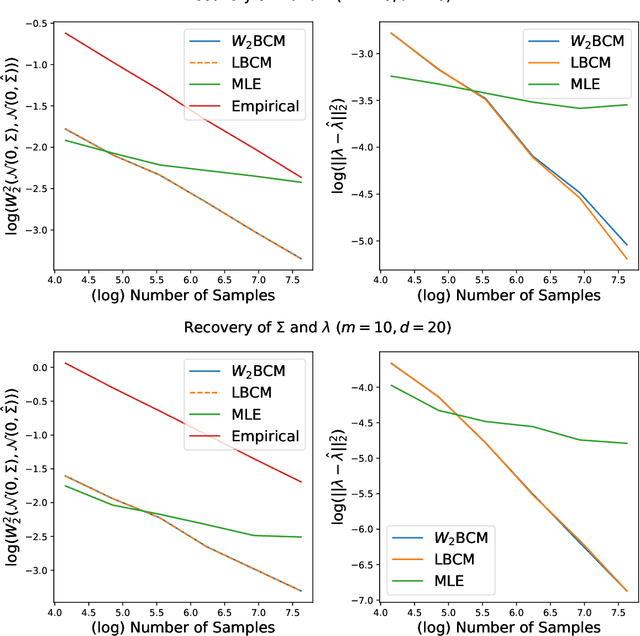
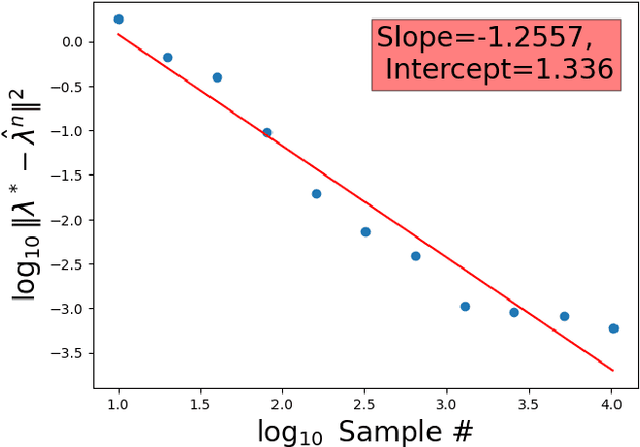
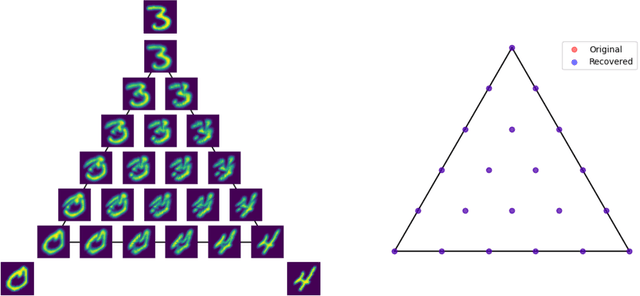
We propose the \textit{linear barycentric coding model (LBCM)} that utilizes the linear optimal transport (LOT) metric for analysis and synthesis of probability measures. We provide a closed-form solution to the variational problem characterizing the probability measures in the LBCM and establish equivalence of the LBCM to the set of Wasserstein-2 barycenters in the special case of compatible measures. Computational methods for synthesizing and analyzing measures in the LBCM are developed with finite sample guarantees. One of our main theoretical contributions is to identify an LBCM, expressed in terms of a simple family, which is sufficient to express all probability measures on the interval $[0,1]$. We show that a natural analogous construction of an LBCM in $\mathbb{R}^2$ fails, and we leave it as an open problem to identify the proper extension in more than one dimension. We conclude by demonstrating the utility of LBCM for covariance estimation and data imputation.

Locality Regularized Reconstruction: Structured Sparsity and Delaunay Triangulations

Linear representation learning is widely studied due to its conceptual simplicity and empirical utility in tasks such as compression, classification, and feature extraction. Given a set of points $[\mathbf{x}_1, \mathbf{x}_2, \ldots, \mathbf{x}_n] = \mathbf{X} \in \mathbb{R}^{d \times n}$ and a vector $\mathbf{y} \in \mathbb{R}^d$, the goal is to find coefficients $\mathbf{w} \in \mathbb{R}^n$ so that $\mathbf{X} \mathbf{w} \approx \mathbf{y}$, subject to some desired structure on $\mathbf{w}$. In this work we seek $\mathbf{w}$ that forms a local reconstruction of $\mathbf{y}$ by solving a regularized least squares regression problem. We obtain local solutions through a locality function that promotes the use of columns of $\mathbf{X}$ that are close to $\mathbf{y}$ when used as a regularization term. We prove that, for all levels of regularization and under a mild condition that the columns of $\mathbf{X}$ have a unique Delaunay triangulation, the optimal coefficients' number of non-zero entries is upper bounded by $d+1$, thereby providing local sparse solutions when $d \ll n$. Under the same condition we also show that for any $\mathbf{y}$ contained in the convex hull of $\mathbf{X}$ there exists a regime of regularization parameter such that the optimal coefficients are supported on the vertices of the Delaunay simplex containing $\mathbf{y}$. This provides an interpretation of the sparsity as having structure obtained implicitly from the Delaunay triangulation of $\mathbf{X}$. We demonstrate that our locality regularized problem can be solved in comparable time to other methods that identify the containing Delaunay simplex.

Superpixel-based and Spatially-regularized Diffusion Learning for Unsupervised Hyperspectral Image Clustering

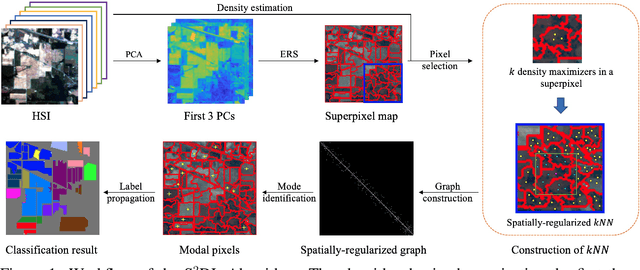
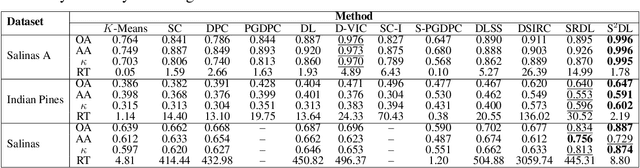
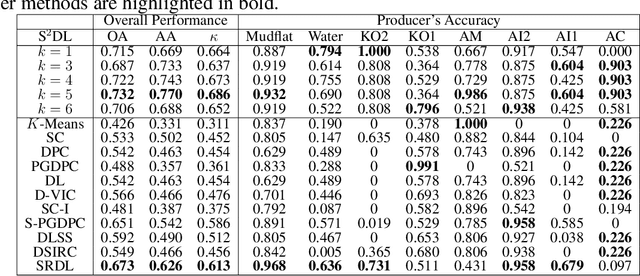
Hyperspectral images (HSIs) provide exceptional spatial and spectral resolution of a scene, crucial for various remote sensing applications. However, the high dimensionality, presence of noise and outliers, and the need for precise labels of HSIs present significant challenges to HSIs analysis, motivating the development of performant HSI clustering algorithms. This paper introduces a novel unsupervised HSI clustering algorithm, Superpixel-based and Spatially-regularized Diffusion Learning (S2DL), which addresses these challenges by incorporating rich spatial information encoded in HSIs into diffusion geometry-based clustering. S2DL employs the Entropy Rate Superpixel (ERS) segmentation technique to partition an image into superpixels, then constructs a spatially-regularized diffusion graph using the most representative high-density pixels. This approach reduces computational burden while preserving accuracy. Cluster modes, serving as exemplars for underlying cluster structure, are identified as the highest-density pixels farthest in diffusion distance from other highest-density pixels. These modes guide the labeling of the remaining representative pixels from ERS superpixels. Finally, majority voting is applied to the labels assigned within each superpixel to propagate labels to the rest of the image. This spatial-spectral approach simultaneously simplifies graph construction, reduces computational cost, and improves clustering performance. S2DL's performance is illustrated with extensive experiments on three publicly available, real-world HSIs: Indian Pines, Salinas, and Salinas A. Additionally, we apply S2DL to landscape-scale, unsupervised mangrove species mapping in the Mai Po Nature Reserve, Hong Kong, using a Gaofen-5 HSI. The success of S2DL in these diverse numerical experiments indicates its efficacy on a wide range of important unsupervised remote sensing analysis tasks.

Estimation of entropy-regularized optimal transport maps between non-compactly supported measures

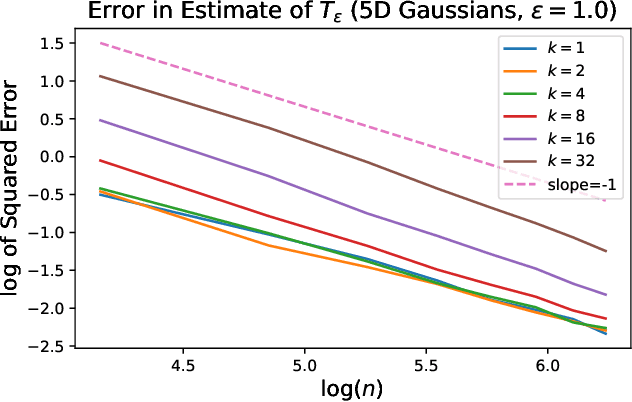
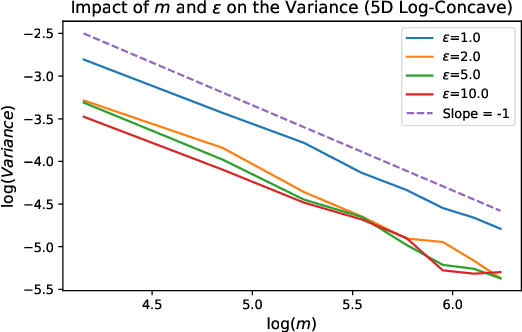
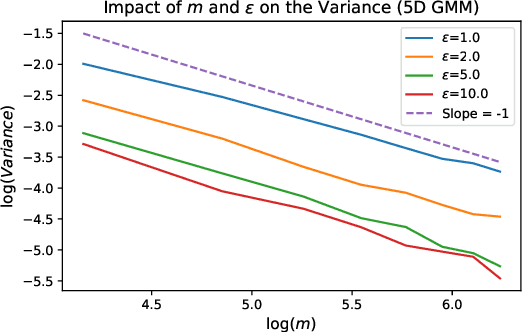
This paper addresses the problem of estimating entropy-regularized optimal transport (EOT) maps with squared-Euclidean cost between source and target measures that are subGaussian. In the case that the target measure is compactly supported or strongly log-concave, we show that for a recently proposed in-sample estimator, the expected squared $L^2$-error decays at least as fast as $O(n^{-1/3})$ where $n$ is the sample size. For the general subGaussian case we show that the expected $L^1$-error decays at least as fast as $O(n^{-1/6})$, and in both cases we have polynomial dependence on the regularization parameter. While these results are suboptimal compared to known results in the case of compactness of both the source and target measures (squared $L^2$-error converging at a rate $O(n^{-1})$) and for when the source is subGaussian while the target is compactly supported (squared $L^2$-error converging at a rate $O(n^{-1/2})$), their importance lie in eliminating the compact support requirements. The proof technique makes use of a bias-variance decomposition where the variance is controlled using standard concentration of measure results and the bias is handled by T1-transport inequalities along with sample complexity results in estimation of EOT cost under subGaussian assumptions. Our experimental results point to a looseness in controlling the variance terms and we conclude by posing several open problems.

Fermat Distances: Metric Approximation, Spectral Convergence, and Clustering Algorithms

We analyze the convergence properties of Fermat distances, a family of density-driven metrics defined on Riemannian manifolds with an associated probability measure. Fermat distances may be defined either on discrete samples from the underlying measure, in which case they are random, or in the continuum setting, in which they are induced by geodesics under a density-distorted Riemannian metric. We prove that discrete, sample-based Fermat distances converge to their continuum analogues in small neighborhoods with a precise rate that depends on the intrinsic dimensionality of the data and the parameter governing the extent of density weighting in Fermat distances. This is done by leveraging novel geometric and statistical arguments in percolation theory that allow for non-uniform densities and curved domains. Our results are then used to prove that discrete graph Laplacians based on discrete, sample-driven Fermat distances converge to corresponding continuum operators. In particular, we show the discrete eigenvalues and eigenvectors converge to their continuum analogues at a dimension-dependent rate, which allows us to interpret the efficacy of discrete spectral clustering using Fermat distances in terms of the resulting continuum limit. The perspective afforded by our discrete-to-continuum Fermat distance analysis leads to new clustering algorithms for data and related insights into efficient computations associated to density-driven spectral clustering. Our theoretical analysis is supported with numerical simulations and experiments on synthetic and real image data.

On Rank Energy Statistics via Optimal Transport: Continuity, Convergence, and Change Point Detection

This paper considers the use of recently proposed optimal transport-based multivariate test statistics, namely rank energy and its variant the soft rank energy derived from entropically regularized optimal transport, for the unsupervised nonparametric change point detection (CPD) problem. We show that the soft rank energy enjoys both fast rates of statistical convergence and robust continuity properties which lead to strong performance on real datasets. Our theoretical analyses remove the need for resampling and out-of-sample extensions previously required to obtain such rates. In contrast the rank energy suffers from the curse of dimensionality in statistical estimation and moreover can signal a change point from arbitrarily small perturbations, which leads to a high rate of false alarms in CPD. Additionally, under mild regularity conditions, we quantify the discrepancy between soft rank energy and rank energy in terms of the regularization parameter. Finally, we show our approach performs favorably in numerical experiments compared to several other optimal transport-based methods as well as maximum mean discrepancy.

Unsupervised Spatial-spectral Hyperspectral Image Reconstruction and Clustering with Diffusion Geometry

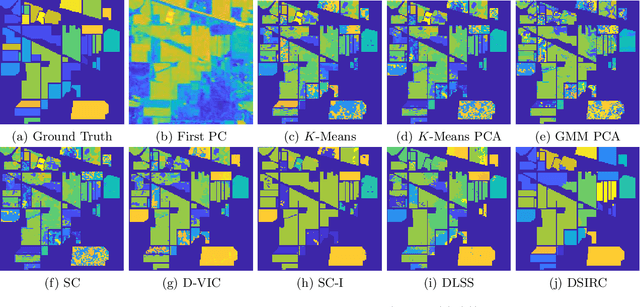
Hyperspectral images, which store a hundred or more spectral bands of reflectance, have become an important data source in natural and social sciences. Hyperspectral images are often generated in large quantities at a relatively coarse spatial resolution. As such, unsupervised machine learning algorithms incorporating known structure in hyperspectral imagery are needed to analyze these images automatically. This work introduces the Spatial-Spectral Image Reconstruction and Clustering with Diffusion Geometry (DSIRC) algorithm for partitioning highly mixed hyperspectral images. DSIRC reduces measurement noise through a shape-adaptive reconstruction procedure. In particular, for each pixel, DSIRC locates spectrally correlated pixels within a data-adaptive spatial neighborhood and reconstructs that pixel's spectral signature using those of its neighbors. DSIRC then locates high-density, high-purity pixels far in diffusion distance (a data-dependent distance metric) from other high-density, high-purity pixels and treats these as cluster exemplars, giving each a unique label. Non-modal pixels are assigned the label of their diffusion distance-nearest neighbor of higher density and purity that is already labeled. Strong numerical results indicate that incorporating spatial information through image reconstruction substantially improves the performance of pixel-wise clustering.

Unsupervised detection of ash dieback disease (Hymenoscyphus fraxineus) using diffusion-based hyperspectral image clustering

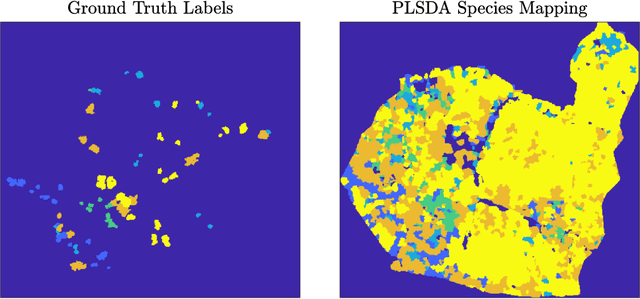
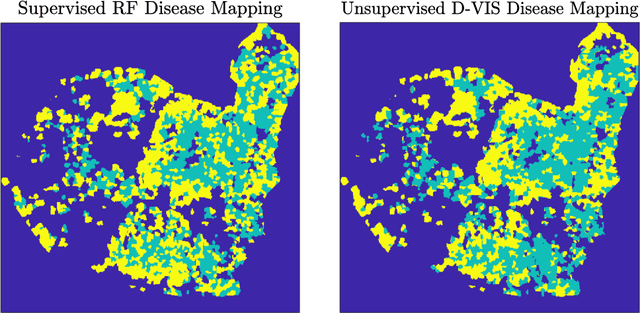
Ash dieback (Hymenoscyphus fraxineus) is an introduced fungal disease that is causing the widespread death of ash trees across Europe. Remote sensing hyperspectral images encode rich structure that has been exploited for the detection of dieback disease in ash trees using supervised machine learning techniques. However, to understand the state of forest health at landscape-scale, accurate unsupervised approaches are needed. This article investigates the use of the unsupervised Diffusion and VCA-Assisted Image Segmentation (D-VIS) clustering algorithm for the detection of ash dieback disease in a forest site near Cambridge, United Kingdom. The unsupervised clustering presented in this work has high overlap with the supervised classification of previous work on this scene (overall accuracy = 71%). Thus, unsupervised learning may be used for the remote detection of ash dieback disease without the need for expert labeling.

Active Diffusion and VCA-Assisted Image Segmentation of Hyperspectral Images

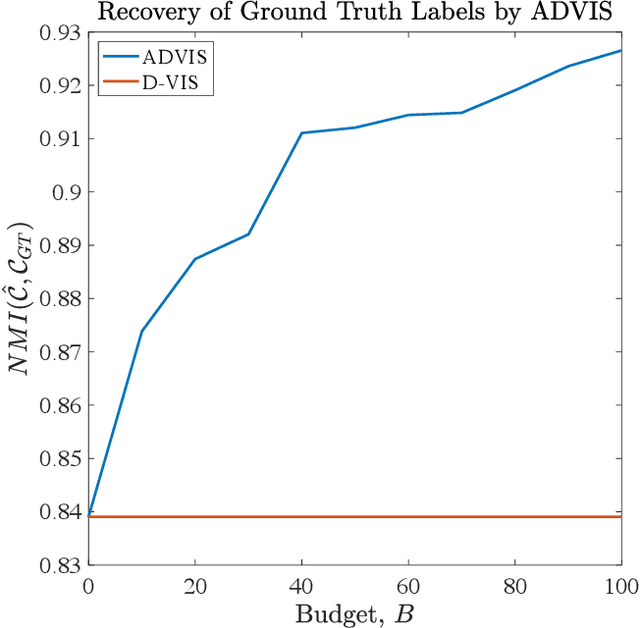
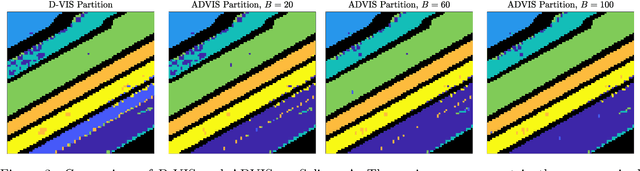
Hyperspectral images encode rich structure that can be exploited for material discrimination by machine learning algorithms. This article introduces the Active Diffusion and VCA-Assisted Image Segmentation (ADVIS) for active material discrimination. ADVIS selects high-purity, high-density pixels that are far in diffusion distance (a data-dependent metric) from other high-purity, high-density pixels in the hyperspectral image. The ground truth labels of these pixels are queried and propagated to the rest of the image. The ADVIS active learning algorithm is shown to strongly outperform its fully unsupervised clustering algorithm counterpart, suggesting that the incorporation of a very small number of carefully-selected ground truth labels can result in substantially superior material discrimination in hyperspectral images.