On Rank Energy Statistics via Optimal Transport: Continuity, Convergence, and Change Point Detection

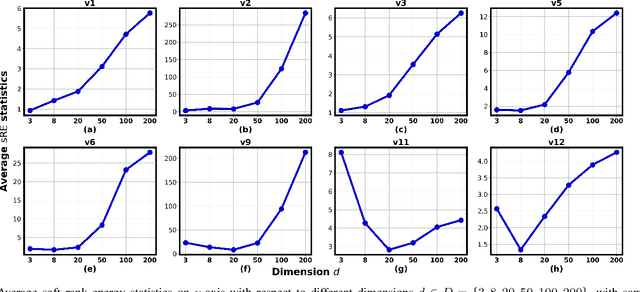
This paper considers the use of recently proposed optimal transport-based multivariate test statistics, namely rank energy and its variant the soft rank energy derived from entropically regularized optimal transport, for the unsupervised nonparametric change point detection (CPD) problem. We show that the soft rank energy enjoys both fast rates of statistical convergence and robust continuity properties which lead to strong performance on real datasets. Our theoretical analyses remove the need for resampling and out-of-sample extensions previously required to obtain such rates. In contrast the rank energy suffers from the curse of dimensionality in statistical estimation and moreover can signal a change point from arbitrarily small perturbations, which leads to a high rate of false alarms in CPD. Additionally, under mild regularity conditions, we quantify the discrepancy between soft rank energy and rank energy in terms of the regularization parameter. Finally, we show our approach performs favorably in numerical experiments compared to several other optimal transport-based methods as well as maximum mean discrepancy.

Robust and efficient change point detection using novel multivariate rank-energy GoF test

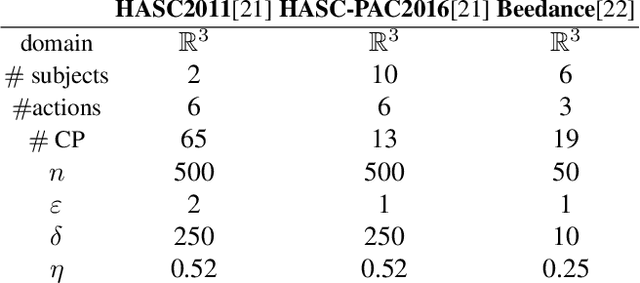
In this paper, we use and further develop upon a recently proposed multivariate, distribution-free Goodness-of-Fit (GoF) test based on the theory of Optimal Transport (OT) called the Rank Energy (RE) [1], for non-parametric and unsupervised Change Point Detection (CPD) in multivariate time series data. We show that directly using RE leads to high sensitivity to very small changes in distributions (causing high false alarms) and it requires large sample complexity and huge computational cost. To alleviate these drawbacks, we propose a new GoF test statistic called as soft-Rank Energy (sRE) that is based on entropy regularized OT and employ it towards CPD. We discuss the advantages of using sRE over RE and demonstrate that the proposed sRE based CPD outperforms all the existing methods in terms of Area Under the Curve (AUC) and F1-score on real and synthetic data sets.

Learning generative models for valid knockoffs using novel multivariate-rank based statistics

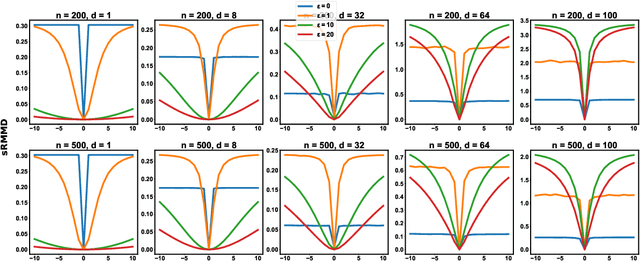
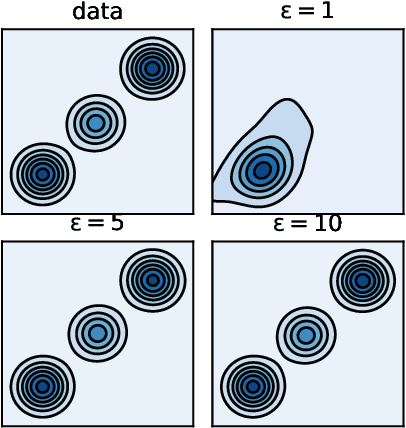
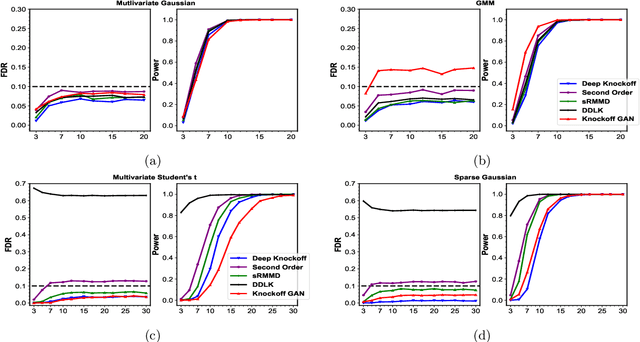
We consider the problem of generating valid knockoffs for knockoff filtering which is a statistical method that provides provable false discovery rate guarantees for any model selection procedure. To this end, we are motivated by recent advances in multivariate distribution-free goodness-of-fit tests namely, the rank energy (RE), that is derived using theoretical results characterizing the optimal maps in the Monge's Optimal Transport (OT) problem. However, direct use of use RE for learning generative models is not feasible because of its high computational and sample complexity, saturation under large support discrepancy between distributions, and non-differentiability in generative parameters. To alleviate these, we begin by proposing a variant of the RE, dubbed as soft rank energy (sRE), and its kernel variant called as soft rank maximum mean discrepancy (sRMMD) using entropic regularization of Monge's OT problem. We then use sRMMD to generate deep knockoffs and show via extensive evaluation that it is a novel and effective method to produce valid knockoffs, achieving comparable, or in some cases improved tradeoffs between detection power Vs false discoveries.

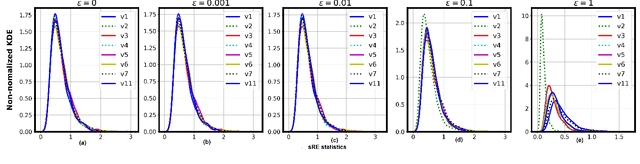
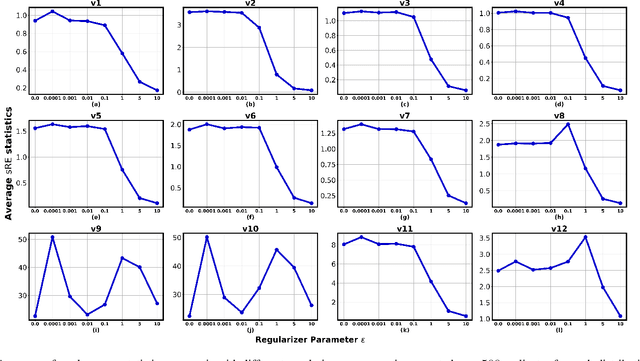
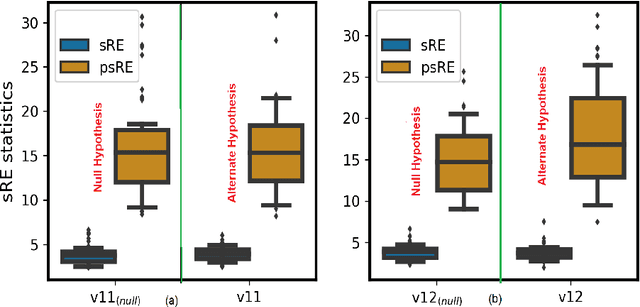
Soft and subspace robust multivariate rank tests based on entropy regularized optimal transport

In this paper, we extend the recently proposed multivariate rank energy distance, based on the theory of optimal transport, for statistical testing of distributional similarity, to soft rank energy distance. Being differentiable, this in turn allows us to extend the rank energy to a subspace robust rank energy distance, dubbed Projected soft-Rank Energy distance, which can be computed via optimization over the Stiefel manifold. We show via experiments that using projected soft rank energy one can trade-off the detection power vs the false alarm via projections onto an appropriately selected low dimensional subspace. We also show the utility of the proposed tests on unsupervised change point detection in multivariate time series data. All codes are publicly available at the link provided in the experiment section.