Linearized Wasserstein Barycenters: Synthesis, Analysis, Representational Capacity, and Applications

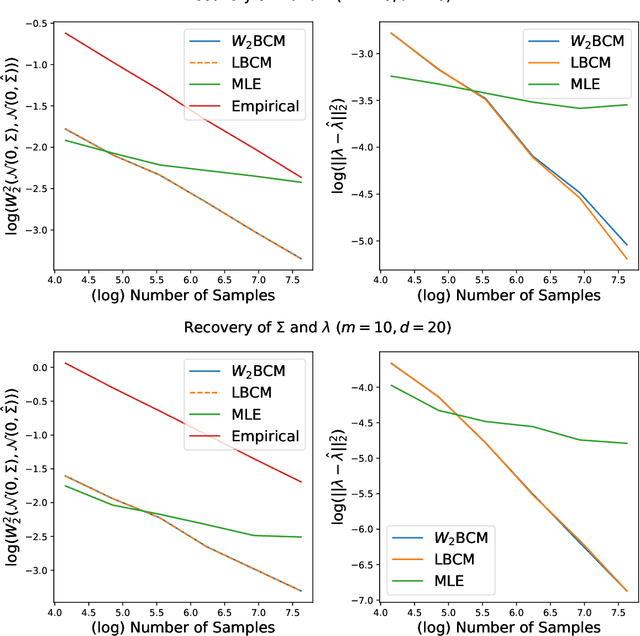
We propose the \textit{linear barycentric coding model (LBCM)} that utilizes the linear optimal transport (LOT) metric for analysis and synthesis of probability measures. We provide a closed-form solution to the variational problem characterizing the probability measures in the LBCM and establish equivalence of the LBCM to the set of Wasserstein-2 barycenters in the special case of compatible measures. Computational methods for synthesizing and analyzing measures in the LBCM are developed with finite sample guarantees. One of our main theoretical contributions is to identify an LBCM, expressed in terms of a simple family, which is sufficient to express all probability measures on the interval $[0,1]$. We show that a natural analogous construction of an LBCM in $\mathbb{R}^2$ fails, and we leave it as an open problem to identify the proper extension in more than one dimension. We conclude by demonstrating the utility of LBCM for covariance estimation and data imputation.

An Optimal Transport Approach for Computing Adversarial Training Lower Bounds in Multiclass Classification

Despite the success of deep learning-based algorithms, it is widely known that neural networks may fail to be robust. A popular paradigm to enforce robustness is adversarial training (AT), however, this introduces many computational and theoretical difficulties. Recent works have developed a connection between AT in the multiclass classification setting and multimarginal optimal transport (MOT), unlocking a new set of tools to study this problem. In this paper, we leverage the MOT connection to propose computationally tractable numerical algorithms for computing universal lower bounds on the optimal adversarial risk and identifying optimal classifiers. We propose two main algorithms based on linear programming (LP) and entropic regularization (Sinkhorn). Our key insight is that one can harmlessly truncate the higher order interactions between classes, preventing the combinatorial run times typically encountered in MOT problems. We validate these results with experiments on MNIST and CIFAR-$10$, which demonstrate the tractability of our approach.

Estimation of entropy-regularized optimal transport maps between non-compactly supported measures

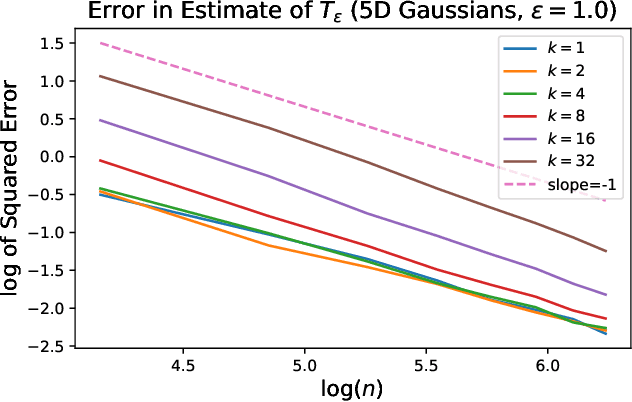
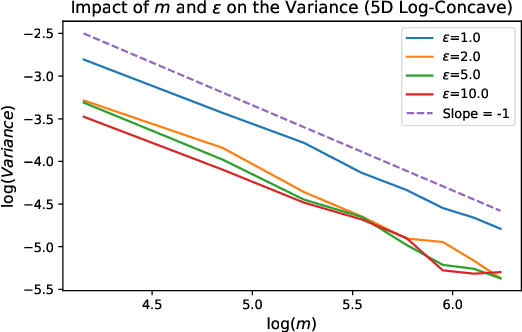
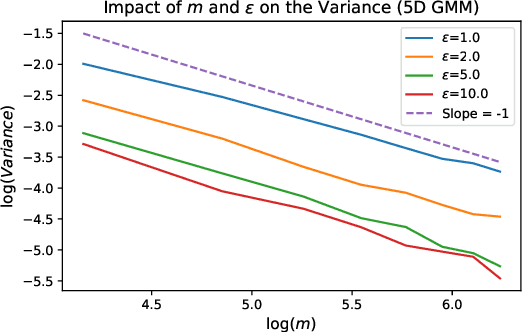
This paper addresses the problem of estimating entropy-regularized optimal transport (EOT) maps with squared-Euclidean cost between source and target measures that are subGaussian. In the case that the target measure is compactly supported or strongly log-concave, we show that for a recently proposed in-sample estimator, the expected squared $L^2$-error decays at least as fast as $O(n^{-1/3})$ where $n$ is the sample size. For the general subGaussian case we show that the expected $L^1$-error decays at least as fast as $O(n^{-1/6})$, and in both cases we have polynomial dependence on the regularization parameter. While these results are suboptimal compared to known results in the case of compactness of both the source and target measures (squared $L^2$-error converging at a rate $O(n^{-1})$) and for when the source is subGaussian while the target is compactly supported (squared $L^2$-error converging at a rate $O(n^{-1/2})$), their importance lie in eliminating the compact support requirements. The proof technique makes use of a bias-variance decomposition where the variance is controlled using standard concentration of measure results and the bias is handled by T1-transport inequalities along with sample complexity results in estimation of EOT cost under subGaussian assumptions. Our experimental results point to a looseness in controlling the variance terms and we conclude by posing several open problems.

On Rank Energy Statistics via Optimal Transport: Continuity, Convergence, and Change Point Detection

This paper considers the use of recently proposed optimal transport-based multivariate test statistics, namely rank energy and its variant the soft rank energy derived from entropically regularized optimal transport, for the unsupervised nonparametric change point detection (CPD) problem. We show that the soft rank energy enjoys both fast rates of statistical convergence and robust continuity properties which lead to strong performance on real datasets. Our theoretical analyses remove the need for resampling and out-of-sample extensions previously required to obtain such rates. In contrast the rank energy suffers from the curse of dimensionality in statistical estimation and moreover can signal a change point from arbitrarily small perturbations, which leads to a high rate of false alarms in CPD. Additionally, under mild regularity conditions, we quantify the discrepancy between soft rank energy and rank energy in terms of the regularization parameter. Finally, we show our approach performs favorably in numerical experiments compared to several other optimal transport-based methods as well as maximum mean discrepancy.

Measure Estimation in the Barycentric Coding Model

This paper considers the problem of measure estimation under the barycentric coding model (BCM), in which an unknown measure is assumed to belong to the set of Wasserstein-2 barycenters of a finite set of known measures. Estimating a measure under this model is equivalent to estimating the unknown barycenteric coordinates. We provide novel geometrical, statistical, and computational insights for measure estimation under the BCM, consisting of three main results. Our first main result leverages the Riemannian geometry of Wasserstein-2 space to provide a procedure for recovering the barycentric coordinates as the solution to a quadratic optimization problem assuming access to the true reference measures. The essential geometric insight is that the parameters of this quadratic problem are determined by inner products between the optimal displacement maps from the given measure to the reference measures defining the BCM. Our second main result then establishes an algorithm for solving for the coordinates in the BCM when all the measures are observed empirically via i.i.d. samples. We prove precise rates of convergence for this algorithm -- determined by the smoothness of the underlying measures and their dimensionality -- thereby guaranteeing its statistical consistency. Finally, we demonstrate the utility of the BCM and associated estimation procedures in three application areas: (i) covariance estimation for Gaussian measures; (ii) image processing; and (iii) natural language processing.