An Optimal Transport Approach for Computing Adversarial Training Lower Bounds in Multiclass Classification

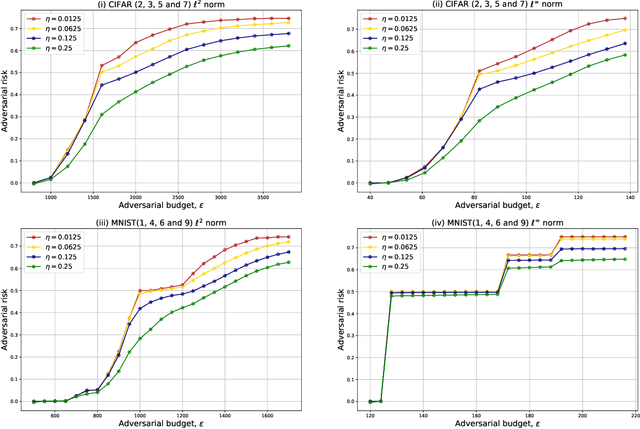
Despite the success of deep learning-based algorithms, it is widely known that neural networks may fail to be robust. A popular paradigm to enforce robustness is adversarial training (AT), however, this introduces many computational and theoretical difficulties. Recent works have developed a connection between AT in the multiclass classification setting and multimarginal optimal transport (MOT), unlocking a new set of tools to study this problem. In this paper, we leverage the MOT connection to propose computationally tractable numerical algorithms for computing universal lower bounds on the optimal adversarial risk and identifying optimal classifiers. We propose two main algorithms based on linear programming (LP) and entropic regularization (Sinkhorn). Our key insight is that one can harmlessly truncate the higher order interactions between classes, preventing the combinatorial run times typically encountered in MOT problems. We validate these results with experiments on MNIST and CIFAR-$10$, which demonstrate the tractability of our approach.

On the existence of solutions to adversarial training in multiclass classification

We study three models of the problem of adversarial training in multiclass classification designed to construct robust classifiers against adversarial perturbations of data in the agnostic-classifier setting. We prove the existence of Borel measurable robust classifiers in each model and provide a unified perspective of the adversarial training problem, expanding the connections with optimal transport initiated by the authors in previous work and developing new connections between adversarial training in the multiclass setting and total variation regularization. As a corollary of our results, we prove the existence of Borel measurable solutions to the agnostic adversarial training problem in the binary classification setting, a result that improves results in the literature of adversarial training, where robust classifiers were only known to exist within the enlarged universal $\sigma$-algebra of the feature space.

The Multimarginal Optimal Transport Formulation of Adversarial Multiclass Classification

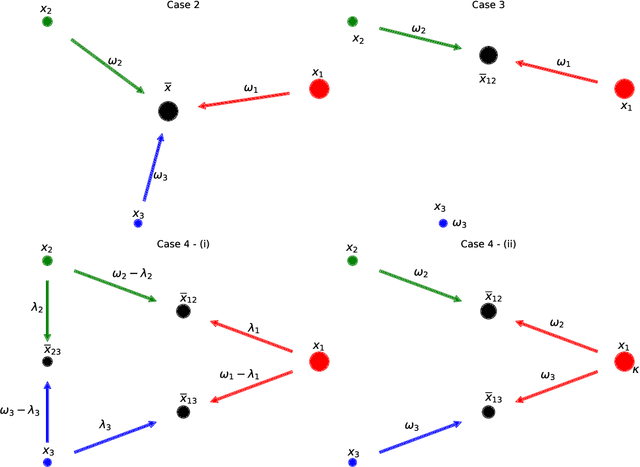
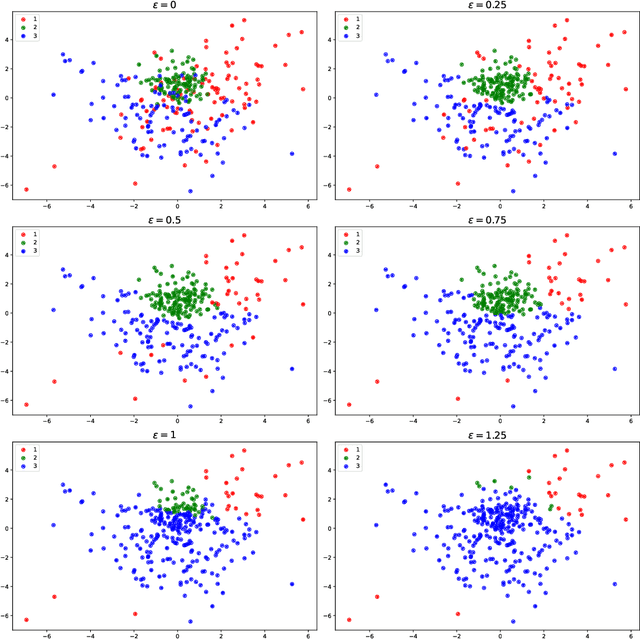
We study a family of adversarial multiclass classification problems and provide equivalent reformulations in terms of: 1) a family of generalized barycenter problems introduced in the paper and 2) a family of multimarginal optimal transport problems where the number of marginals is equal to the number of classes in the original classification problem. These new theoretical results reveal a rich geometric structure of adversarial learning problems in multiclass classification and extend recent results restricted to the binary classification setting. A direct computational implication of our results is that by solving either the barycenter problem and its dual, or the MOT problem and its dual, we can recover the optimal robust classification rule and the optimal adversarial strategy for the original adversarial problem. Examples with synthetic and real data illustrate our results.