Lower Bounds on Adversarial Robustness for Multiclass Classification with General Loss Functions

We consider adversarially robust classification in a multiclass setting under arbitrary loss functions and derive dual and barycentric reformulations of the corresponding learner-agnostic robust risk minimization problem. We provide explicit characterizations for important cases such as the cross-entropy loss, loss functions with a power form, and the quadratic loss, extending in this way available results for the 0-1 loss. These reformulations enable efficient computation of sharp lower bounds for adversarial risks and facilitate the design of robust classifiers beyond the 0-1 loss setting. Our paper uncovers interesting connections between adversarial robustness, $\alpha$-fair packing problems, and generalized barycenter problems for arbitrary positive measures where Kullback-Leibler and Tsallis entropies are used as penalties. Our theoretical results are accompanied with illustrative numerical experiments where we obtain tighter lower bounds for adversarial risks with the cross-entropy loss function.

Vector valued optimal transport: from dynamic to static formulations

Motivated by applications in classification of vector valued measures and multispecies PDE, we develop a theory that unifies existing notions of vector valued optimal transport, from dynamic formulations (\`a la Benamou-Brenier) to static formulations (\`a la Kantorovich). In our framework, vector valued measures are modeled as probability measures on a product space $\mathbb{R}^d \times G$, where $G$ is a weighted graph over a finite set of nodes and the graph geometry strongly influences the associated dynamic and static distances. We obtain sharp inequalities relating four notions of vector valued optimal transport and prove that the distances are mutually bi-H\"older equivalent. We discuss the theoretical and practical advantages of each metric and indicate potential applications in multispecies PDE and data analysis. In particular, one of the static formulations discussed in the paper is amenable to linearization, a technique that has been explored in recent years to accelerate the computation of pairwise optimal transport distances.

Defending Against Diverse Attacks in Federated Learning Through Consensus-Based Bi-Level Optimization

Adversarial attacks pose significant challenges in many machine learning applications, particularly in the setting of distributed training and federated learning, where malicious agents seek to corrupt the training process with the goal of jeopardizing and compromising the performance and reliability of the final models. In this paper, we address the problem of robust federated learning in the presence of such attacks by formulating the training task as a bi-level optimization problem. We conduct a theoretical analysis of the resilience of consensus-based bi-level optimization (CB$^2$O), an interacting multi-particle metaheuristic optimization method, in adversarial settings. Specifically, we provide a global convergence analysis of CB$^2$O in mean-field law in the presence of malicious agents, demonstrating the robustness of CB$^2$O against a diverse range of attacks. Thereby, we offer insights into how specific hyperparameter choices enable to mitigate adversarial effects. On the practical side, we extend CB$^2$O to the clustered federated learning setting by proposing FedCB$^2$O, a novel interacting multi-particle system, and design a practical algorithm that addresses the demands of real-world applications. Extensive experiments demonstrate the robustness of the FedCB$^2$O algorithm against label-flipping attacks in decentralized clustered federated learning scenarios, showcasing its effectiveness in practical contexts.

Fermat Distances: Metric Approximation, Spectral Convergence, and Clustering Algorithms

We analyze the convergence properties of Fermat distances, a family of density-driven metrics defined on Riemannian manifolds with an associated probability measure. Fermat distances may be defined either on discrete samples from the underlying measure, in which case they are random, or in the continuum setting, in which they are induced by geodesics under a density-distorted Riemannian metric. We prove that discrete, sample-based Fermat distances converge to their continuum analogues in small neighborhoods with a precise rate that depends on the intrinsic dimensionality of the data and the parameter governing the extent of density weighting in Fermat distances. This is done by leveraging novel geometric and statistical arguments in percolation theory that allow for non-uniform densities and curved domains. Our results are then used to prove that discrete graph Laplacians based on discrete, sample-driven Fermat distances converge to corresponding continuum operators. In particular, we show the discrete eigenvalues and eigenvectors converge to their continuum analogues at a dimension-dependent rate, which allows us to interpret the efficacy of discrete spectral clustering using Fermat distances in terms of the resulting continuum limit. The perspective afforded by our discrete-to-continuum Fermat distance analysis leads to new clustering algorithms for data and related insights into efficient computations associated to density-driven spectral clustering. Our theoretical analysis is supported with numerical simulations and experiments on synthetic and real image data.

It begins with a boundary: A geometric view on probabilistically robust learning

Although deep neural networks have achieved super-human performance on many classification tasks, they often exhibit a worrying lack of robustness towards adversarially generated examples. Thus, considerable effort has been invested into reformulating Empirical Risk Minimization (ERM) into an adversarially robust framework. Recently, attention has shifted towards approaches which interpolate between the robustness offered by adversarial training and the higher clean accuracy and faster training times of ERM. In this paper, we take a fresh and geometric view on one such method -- Probabilistically Robust Learning (PRL) (Robey et al., ICML, 2022). We propose a geometric framework for understanding PRL, which allows us to identify a subtle flaw in its original formulation and to introduce a family of probabilistic nonlocal perimeter functionals to address this. We prove existence of solutions using novel relaxation methods and study properties as well as local limits of the introduced perimeters.

Wasserstein Barycenter-based Model Fusion and Linear Mode Connectivity of Neural Networks

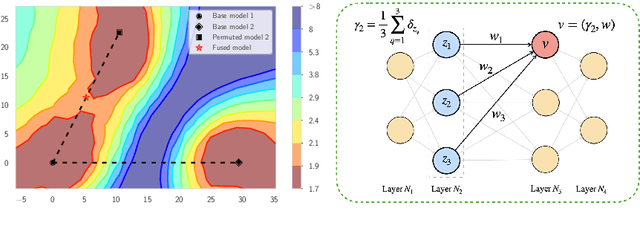
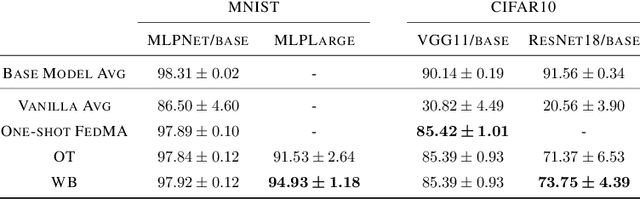
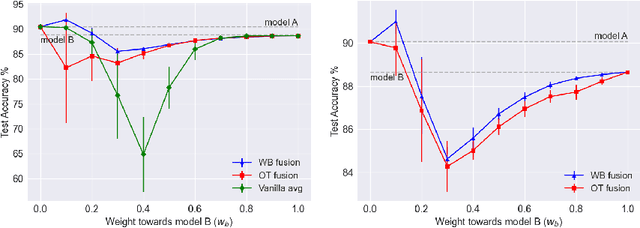
Based on the concepts of Wasserstein barycenter (WB) and Gromov-Wasserstein barycenter (GWB), we propose a unified mathematical framework for neural network (NN) model fusion and utilize it to reveal new insights about the linear mode connectivity of SGD solutions. In our framework, the fusion occurs in a layer-wise manner and builds on an interpretation of a node in a network as a function of the layer preceding it. The versatility of our mathematical framework allows us to talk about model fusion and linear mode connectivity for a broad class of NNs, including fully connected NN, CNN, ResNet, RNN, and LSTM, in each case exploiting the specific structure of the network architecture. We present extensive numerical experiments to: 1) illustrate the strengths of our approach in relation to other model fusion methodologies and 2) from a certain perspective, provide new empirical evidence for recent conjectures which say that two local minima found by gradient-based methods end up lying on the same basin of the loss landscape after a proper permutation of weights is applied to one of the models.

Rates of Convergence for Regression with the Graph Poly-Laplacian

In the (special) smoothing spline problem one considers a variational problem with a quadratic data fidelity penalty and Laplacian regularisation. Higher order regularity can be obtained via replacing the Laplacian regulariser with a poly-Laplacian regulariser. The methodology is readily adapted to graphs and here we consider graph poly-Laplacian regularisation in a fully supervised, non-parametric, noise corrupted, regression problem. In particular, given a dataset $\{x_i\}_{i=1}^n$ and a set of noisy labels $\{y_i\}_{i=1}^n\subset\mathbb{R}$ we let $u_n:\{x_i\}_{i=1}^n\to\mathbb{R}$ be the minimiser of an energy which consists of a data fidelity term and an appropriately scaled graph poly-Laplacian term. When $y_i = g(x_i)+\xi_i$, for iid noise $\xi_i$, and using the geometric random graph, we identify (with high probability) the rate of convergence of $u_n$ to $g$ in the large data limit $n\to\infty$. Furthermore, our rate, up to logarithms, coincides with the known rate of convergence in the usual smoothing spline model.

The Geometry of Adversarial Training in Binary Classification

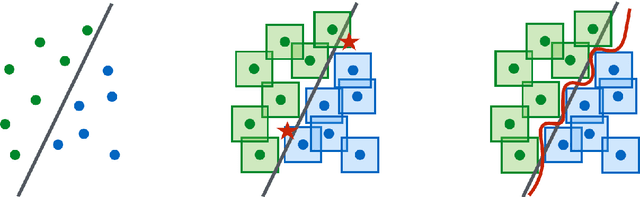
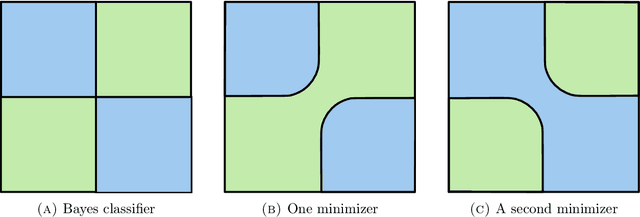
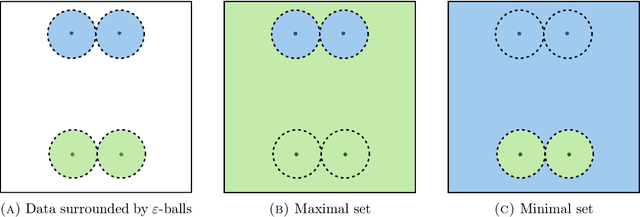
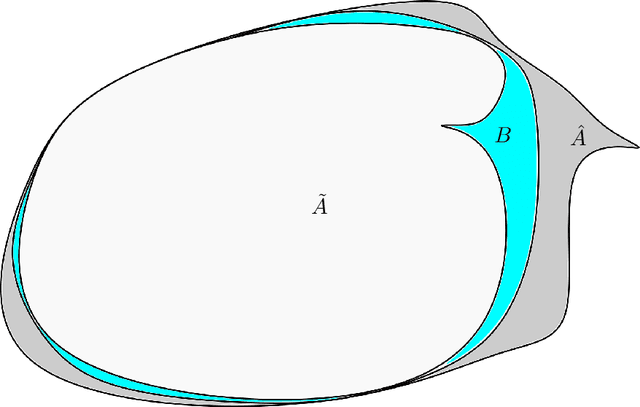
We establish an equivalence between a family of adversarial training problems for non-parametric binary classification and a family of regularized risk minimization problems where the regularizer is a nonlocal perimeter functional. The resulting regularized risk minimization problems admit exact convex relaxations of the type $L^1+$ (nonlocal) $\operatorname{TV}$, a form frequently studied in image analysis and graph-based learning. A rich geometric structure is revealed by this reformulation which in turn allows us to establish a series of properties of optimal solutions of the original problem, including the existence of minimal and maximal solutions (interpreted in a suitable sense), and the existence of regular solutions (also interpreted in a suitable sense). In addition, we highlight how the connection between adversarial training and perimeter minimization problems provides a novel, directly interpretable, statistical motivation for a family of regularized risk minimization problems involving perimeter/total variation. The majority of our theoretical results are independent of the distance used to define adversarial attacks.

Clustering dynamics on graphs: from spectral clustering to mean shift through Fokker-Planck interpolation

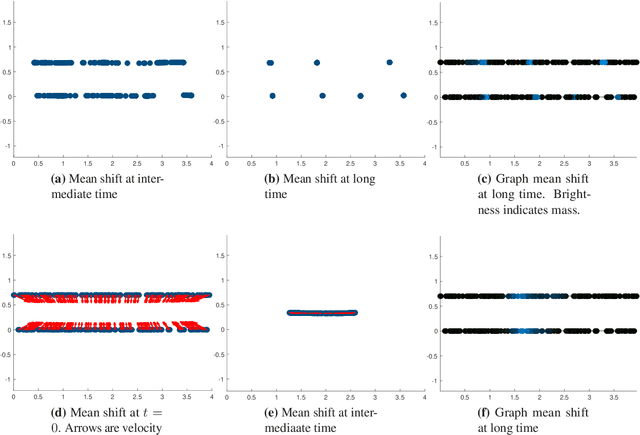
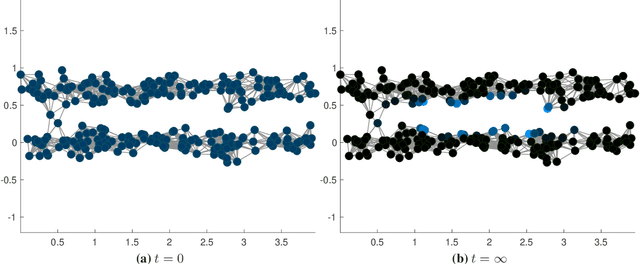
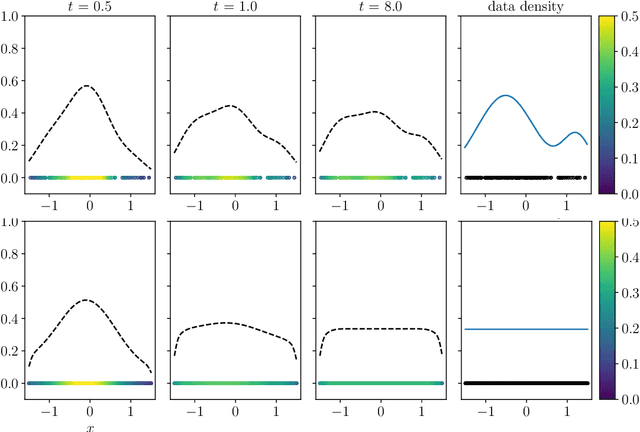
In this work we build a unifying framework to interpolate between density-driven and geometry-based algorithms for data clustering, and specifically, to connect the mean shift algorithm with spectral clustering at discrete and continuum levels. We seek this connection through the introduction of Fokker-Planck equations on data graphs. Besides introducing new forms of mean shift algorithms on graphs, we provide new theoretical insights on the behavior of the family of diffusion maps in the large sample limit as well as provide new connections between diffusion maps and mean shift dynamics on a fixed graph. Several numerical examples illustrate our theoretical findings and highlight the benefits of interpolating density-driven and geometry-based clustering algorithms.

A variational approach to the consistency of spectral clustering

This paper establishes the consistency of spectral approaches to data clustering. We consider clustering of point clouds obtained as samples of a ground-truth measure. A graph representing the point cloud is obtained by assigning weights to edges based on the distance between the points they connect. We investigate the spectral convergence of both unnormalized and normalized graph Laplacians towards the appropriate operators in the continuum domain. We obtain sharp conditions on how the connectivity radius can be scaled with respect to the number of sample points for the spectral convergence to hold. We also show that the discrete clusters obtained via spectral clustering converge towards a continuum partition of the ground truth measure. Such continuum partition minimizes a functional describing the continuum analogue of the graph-based spectral partitioning. Our approach, based on variational convergence, is general and flexible.