Wasserstein Barycenter-based Model Fusion and Linear Mode Connectivity of Neural Networks
Paper and Code
Oct 13, 2022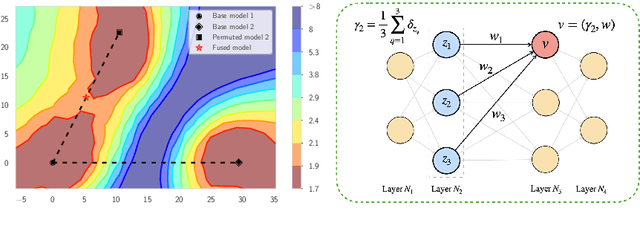
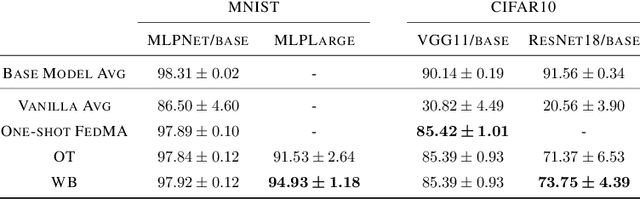
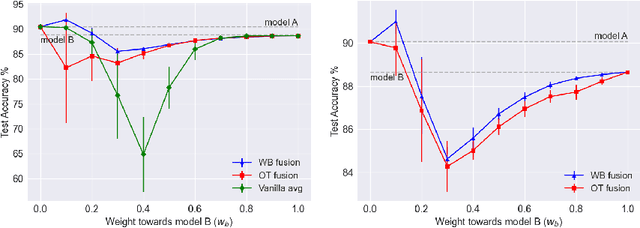

Based on the concepts of Wasserstein barycenter (WB) and Gromov-Wasserstein barycenter (GWB), we propose a unified mathematical framework for neural network (NN) model fusion and utilize it to reveal new insights about the linear mode connectivity of SGD solutions. In our framework, the fusion occurs in a layer-wise manner and builds on an interpretation of a node in a network as a function of the layer preceding it. The versatility of our mathematical framework allows us to talk about model fusion and linear mode connectivity for a broad class of NNs, including fully connected NN, CNN, ResNet, RNN, and LSTM, in each case exploiting the specific structure of the network architecture. We present extensive numerical experiments to: 1) illustrate the strengths of our approach in relation to other model fusion methodologies and 2) from a certain perspective, provide new empirical evidence for recent conjectures which say that two local minima found by gradient-based methods end up lying on the same basin of the loss landscape after a proper permutation of weights is applied to one of the models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge