A Momentum Accelerated Algorithm for ReLU-based Nonlinear Matrix Decomposition

Recently, there has been a growing interest in the exploration of Nonlinear Matrix Decomposition (NMD) due to its close ties with neural networks. NMD aims to find a low-rank matrix from a sparse nonnegative matrix with a per-element nonlinear function. A typical choice is the Rectified Linear Unit (ReLU) activation function. To address over-fitting in the existing ReLU-based NMD model (ReLU-NMD), we propose a Tikhonov regularized ReLU-NMD model, referred to as ReLU-NMD-T. Subsequently, we introduce a momentum accelerated algorithm for handling the ReLU-NMD-T model. A distinctive feature, setting our work apart from most existing studies, is the incorporation of both positive and negative momentum parameters in our algorithm. Our numerical experiments on real-world datasets show the effectiveness of the proposed model and algorithm. Moreover, the code is available at https://github.com/nothing2wang/NMD-TM.

An inexact proximal majorization-minimization Algorithm for remote sensing image stripe noise removal

The stripe noise existing in remote sensing images badly degrades the visual quality and restricts the precision of data analysis. Therefore, many destriping models have been proposed in recent years. In contrast to these existing models, in this paper, we propose a nonconvex model with a DC function (i.e., the difference of convex functions) structure to remove the strip noise. To solve this model, we make use of the DC structure and apply an inexact proximal majorization-minimization algorithm with each inner subproblem solved by the alternating direction method of multipliers. It deserves mentioning that we design an implementable stopping criterion for the inner subproblem, while the convergence can still be guaranteed. Numerical experiments demonstrate the superiority of the proposed model and algorithm.

It begins with a boundary: A geometric view on probabilistically robust learning

Although deep neural networks have achieved super-human performance on many classification tasks, they often exhibit a worrying lack of robustness towards adversarially generated examples. Thus, considerable effort has been invested into reformulating Empirical Risk Minimization (ERM) into an adversarially robust framework. Recently, attention has shifted towards approaches which interpolate between the robustness offered by adversarial training and the higher clean accuracy and faster training times of ERM. In this paper, we take a fresh and geometric view on one such method -- Probabilistically Robust Learning (PRL) (Robey et al., ICML, 2022). We propose a geometric framework for understanding PRL, which allows us to identify a subtle flaw in its original formulation and to introduce a family of probabilistic nonlocal perimeter functionals to address this. We prove existence of solutions using novel relaxation methods and study properties as well as local limits of the introduced perimeters.

A sparse semismooth Newton based augmented Lagrangian method for large-scale support vector machines

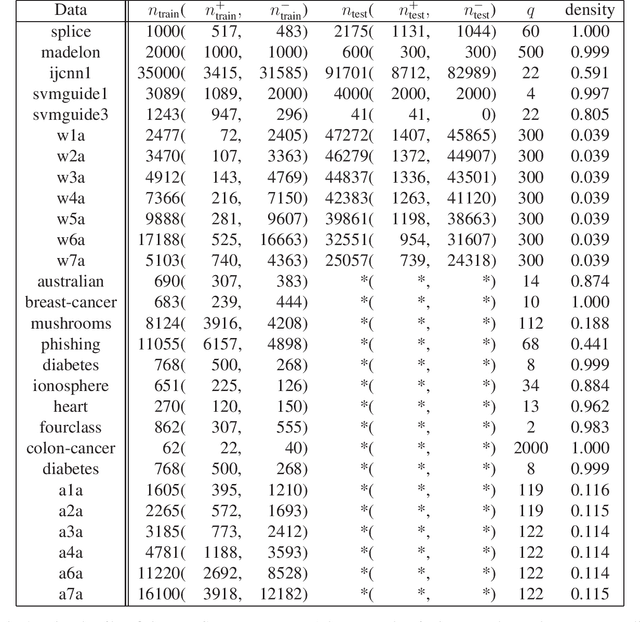
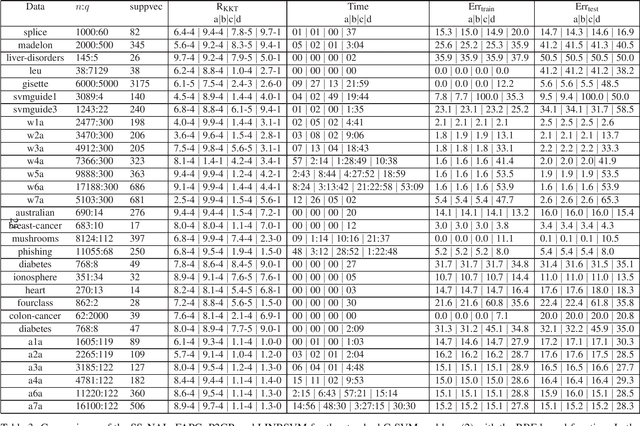
Support vector machines (SVMs) are successful modeling and prediction tools with a variety of applications. Previous work has demonstrated the superiority of the SVMs in dealing with the high dimensional, low sample size problems. However, the numerical difficulties of the SVMs will become severe with the increase of the sample size. Although there exist many solvers for the SVMs, only few of them are designed by exploiting the special structures of the SVMs. In this paper, we propose a highly efficient sparse semismooth Newton based augmented Lagrangian method for solving a large-scale convex quadratic programming problem with a linear equality constraint and a simple box constraint, which is generated from the dual problems of the SVMs. By leveraging the primal-dual error bound result, the fast local convergence rate of the augmented Lagrangian method can be guaranteed. Furthermore, by exploiting the second-order sparsity of the problem when using the semismooth Newton method, the algorithm can efficiently solve the aforementioned difficult problems. Finally, numerical comparisons demonstrate that the proposed algorithm outperforms the current state-of-the-art solvers for the large-scale SVMs.