Neural Network Training via Stochastic Alternating Minimization with Trainable Step Sizes

The training of deep neural networks is inherently a nonconvex optimization problem, yet standard approaches such as stochastic gradient descent (SGD) require simultaneous updates to all parameters, often leading to unstable convergence and high computational cost. To address these issues, we propose a novel method, Stochastic Alternating Minimization with Trainable Step Sizes (SAMT), which updates network parameters in an alternating manner by treating the weights of each layer as a block. By decomposing the overall optimization into sub-problems corresponding to different blocks, this block-wise alternating strategy reduces per-step computational overhead and enhances training stability in nonconvex settings. To fully leverage these benefits, inspired by meta-learning, we proposed a novel adaptive step size strategy to incorporate into the sub-problem solving steps of alternating updates. It supports different types of trainable step sizes, including but not limited to scalar, element-wise, row-wise, and column-wise, enabling adaptive step size selection tailored to each block via meta-learning. We further provide a theoretical convergence guarantee for the proposed algorithm, establishing its optimization soundness. Extensive experiments for multiple benchmarks demonstrate that SAMT achieves better generalization performance with fewer parameter updates compared to state-of-the-art methods, highlighting its effectiveness and potential in neural network optimization.

A Triple-Inertial Accelerated Alternating Optimization Method for Deep Learning Training

The stochastic gradient descent (SGD) algorithm has achieved remarkable success in training deep learning models. However, it has several limitations, including susceptibility to vanishing gradients, sensitivity to input data, and a lack of robust theoretical guarantees. In recent years, alternating minimization (AM) methods have emerged as a promising alternative for model training by employing gradient-free approaches to iteratively update model parameters. Despite their potential, these methods often exhibit slow convergence rates. To address this challenge, we propose a novel Triple-Inertial Accelerated Alternating Minimization (TIAM) framework for neural network training. The TIAM approach incorporates a triple-inertial acceleration strategy with a specialized approximation method, facilitating targeted acceleration of different terms in each sub-problem optimization. This integration improves the efficiency of convergence, achieving superior performance with fewer iterations. Additionally, we provide a convergence analysis of the TIAM algorithm, including its global convergence properties and convergence rate. Extensive experiments validate the effectiveness of the TIAM method, showing significant improvements in generalization capability and computational efficiency compared to existing approaches, particularly when applied to the rectified linear unit (ReLU) and its variants.

Enhancing Socially-Aware Robot Navigation through Bidirectional Natural Language Conversation

Robot navigation is an important research field with applications in various domains. However, traditional approaches often prioritize efficiency and obstacle avoidance, neglecting a nuanced understanding of human behavior or intent in shared spaces. With the rise of service robots, there's an increasing emphasis on endowing robots with the capability to navigate and interact in complex real-world environments. Socially aware navigation has recently become a key research area. However, existing work either predicts pedestrian movements or simply emits alert signals to pedestrians, falling short of facilitating genuine interactions between humans and robots. In this paper, we introduce the Hybrid Soft Actor-Critic with Large Language Model (HSAC-LLM), an innovative model designed for socially-aware navigation in robots. This model seamlessly integrates deep reinforcement learning with large language models, enabling it to predict both continuous and discrete actions for navigation. Notably, HSAC-LLM facilitates bidirectional interaction based on natural language with pedestrian models. When a potential collision with pedestrians is detected, the robot can initiate or respond to communications with pedestrians, obtaining and executing subsequent avoidance strategies. Experimental results in 2D simulation, the Gazebo environment, and the real-world environment demonstrate that HSAC-LLM not only efficiently enables interaction with humans but also exhibits superior performance in navigation and obstacle avoidance compared to state-of-the-art DRL algorithms. We believe this innovative paradigm opens up new avenues for effective and socially aware human-robot interactions in dynamic environments. Videos are available at https://hsacllm.github.io/.

An Inexact Manifold Augmented Lagrangian Method for Adaptive Sparse Canonical Correlation Analysis with Trace Lasso Regularization

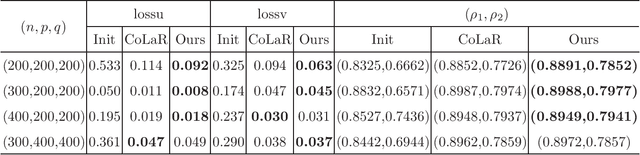
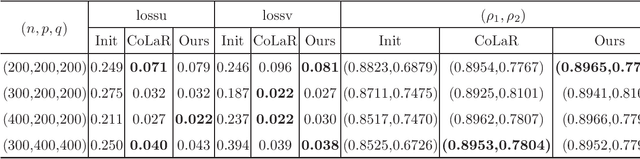
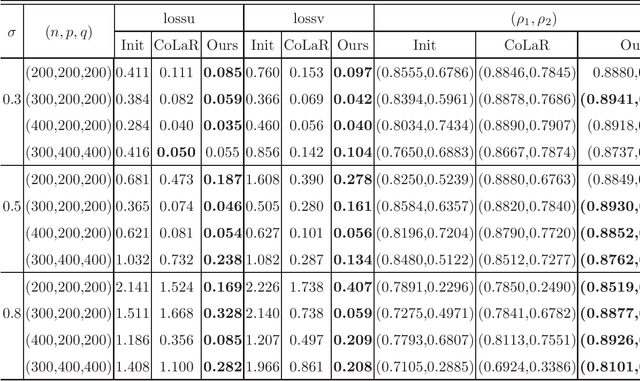
Canonical correlation analysis (CCA for short) describes the relationship between two sets of variables by finding some linear combinations of these variables that maximizing the correlation coefficient. However, in high-dimensional settings where the number of variables exceeds sample size, or in the case of that the variables are highly correlated, the traditional CCA is no longer appropriate. In this paper, an adaptive sparse version of CCA (ASCCA for short) is proposed by using the trace Lasso regularization. The proposed ASCCA reduces the instability of the estimator when the covariates are highly correlated, and thus improves its interpretation. The ASCCA is further reformulated to an optimization problem on Riemannian manifolds, and an manifold inexact augmented Lagrangian method is then proposed for the resulting optimization problem. The performance of the ASCCA is compared with the other sparse CCA techniques in different simulation settings, which illustrates that the ASCCA is feasible and efficient.