An Inexact Manifold Augmented Lagrangian Method for Adaptive Sparse Canonical Correlation Analysis with Trace Lasso Regularization

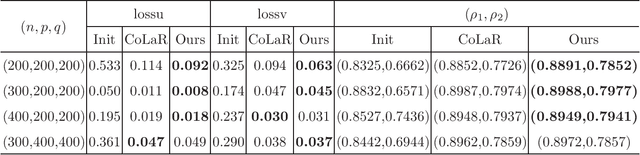
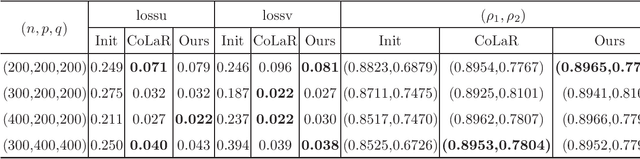
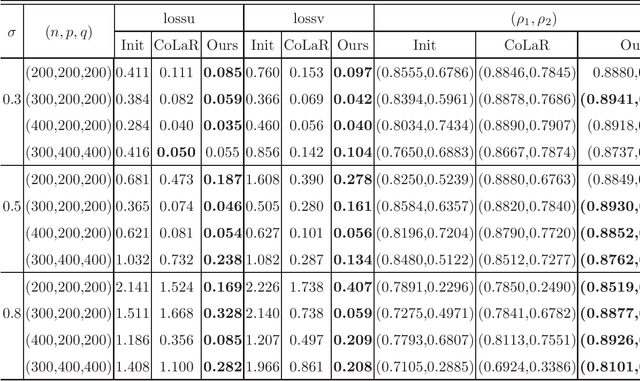
Canonical correlation analysis (CCA for short) describes the relationship between two sets of variables by finding some linear combinations of these variables that maximizing the correlation coefficient. However, in high-dimensional settings where the number of variables exceeds sample size, or in the case of that the variables are highly correlated, the traditional CCA is no longer appropriate. In this paper, an adaptive sparse version of CCA (ASCCA for short) is proposed by using the trace Lasso regularization. The proposed ASCCA reduces the instability of the estimator when the covariates are highly correlated, and thus improves its interpretation. The ASCCA is further reformulated to an optimization problem on Riemannian manifolds, and an manifold inexact augmented Lagrangian method is then proposed for the resulting optimization problem. The performance of the ASCCA is compared with the other sparse CCA techniques in different simulation settings, which illustrates that the ASCCA is feasible and efficient.