Decentralized Riemannian natural gradient methods with Kronecker-product approximations

With a computationally efficient approximation of the second-order information, natural gradient methods have been successful in solving large-scale structured optimization problems. We study the natural gradient methods for the large-scale decentralized optimization problems on Riemannian manifolds, where the local objective function defined by the local dataset is of a log-probability type. By utilizing the structure of the Riemannian Fisher information matrix (RFIM), we present an efficient decentralized Riemannian natural gradient descent (DRNGD) method. To overcome the communication issue of the high-dimension RFIM, we consider a class of structured problems for which the RFIM can be approximated by a Kronecker product of two low-dimension matrices. By performing the communications over the Kronecker factors, a high-quality approximation of the RFIM can be obtained in a low cost. We prove that DRNGD converges to a stationary point with the best-known rate of $\mathcal{O}(1/K)$. Numerical experiments demonstrate the efficiency of our proposed method compared with the state-of-the-art ones. To the best of our knowledge, this is the first Riemannian second-order method for solving decentralized manifold optimization problems.

An Inexact Manifold Augmented Lagrangian Method for Adaptive Sparse Canonical Correlation Analysis with Trace Lasso Regularization

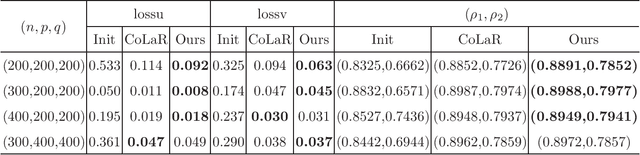
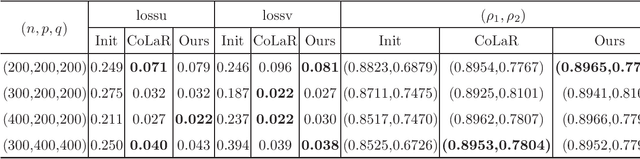
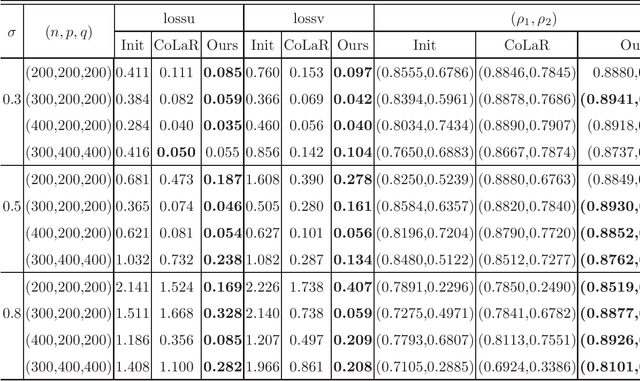
Canonical correlation analysis (CCA for short) describes the relationship between two sets of variables by finding some linear combinations of these variables that maximizing the correlation coefficient. However, in high-dimensional settings where the number of variables exceeds sample size, or in the case of that the variables are highly correlated, the traditional CCA is no longer appropriate. In this paper, an adaptive sparse version of CCA (ASCCA for short) is proposed by using the trace Lasso regularization. The proposed ASCCA reduces the instability of the estimator when the covariates are highly correlated, and thus improves its interpretation. The ASCCA is further reformulated to an optimization problem on Riemannian manifolds, and an manifold inexact augmented Lagrangian method is then proposed for the resulting optimization problem. The performance of the ASCCA is compared with the other sparse CCA techniques in different simulation settings, which illustrates that the ASCCA is feasible and efficient.