Exactly or Approximately Wasserstein Distributionally Robust Estimation According to Wasserstein Radii Being Small or Large

This paper primarily considers the robust estimation problem under Wasserstein distance constraints on the parameter and noise distributions in the linear measurement model with additive noise, which can be formulated as an infinite-dimensional nonconvex minimax problem. We prove that the existence of a saddle point for this problem is equivalent to that for a finite-dimensional minimax problem, and give a counterexample demonstrating that the saddle point may not exist. Motivated by this observation, we present a verifiable necessary and sufficient condition whose parameters can be derived from a convex problem and its dual. Additionally, we also introduce a simplified sufficient condition, which intuitively indicates that when the Wasserstein radii are small enough, the saddle point always exists. In the absence of the saddle point, we solve an finite-dimensional nonconvex minimax problem, obtained by restricting the estimator to be linear. Its optimal value establishes an upper bound on the robust estimation problem, while its optimal solution yields a robust linear estimator. Numerical experiments are also provided to validate our theoretical results.

Decentralized Equalization for Massive MIMO Systems With Colored Noise Samples

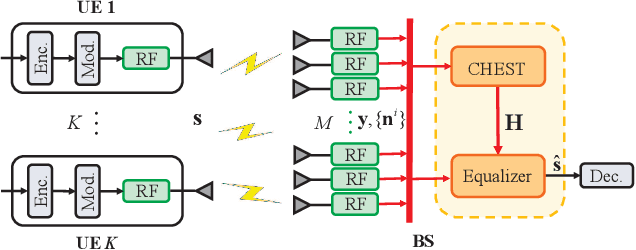
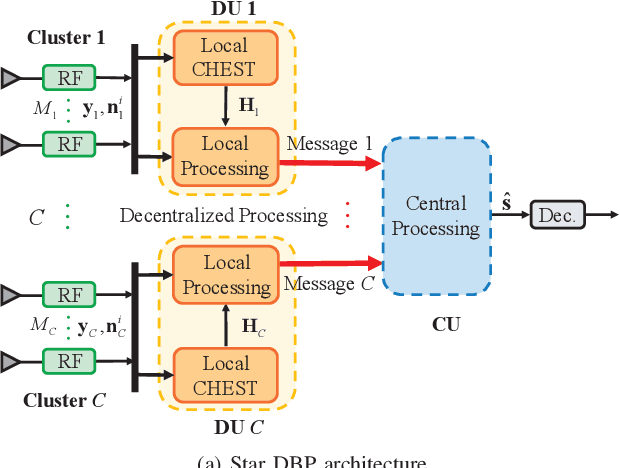
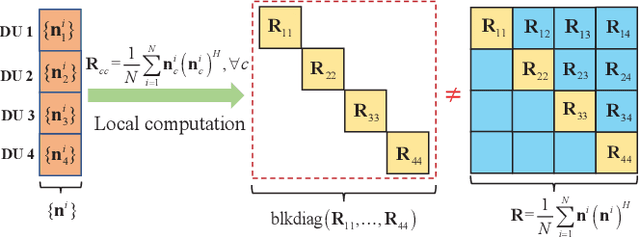
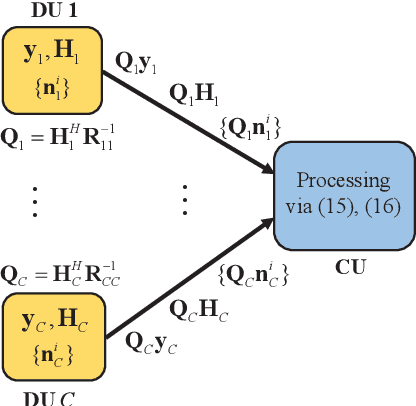
Recently, the decentralized baseband processing (DBP) paradigm and relevant detection methods have been proposed to enable extremely large-scale massive multiple-input multiple-output technology. Under the DBP architecture, base station antennas are divided into several independent clusters, each connected to a local computing fabric. However, current detection methods tailored to DBP only consider ideal white Gaussian noise scenarios, while in practice, the noise is often colored due to interference from neighboring cells. Moreover, in the DBP architecture, linear minimum mean-square error (LMMSE) detection methods rely on the estimation of the noise covariance matrix through averaging distributedly stored noise samples. This presents a significant challenge for decentralized LMMSE-based equalizer design. To address this issue, this paper proposes decentralized LMMSE equalization methods under colored noise scenarios for both star and daisy chain DBP architectures. Specifically, we first propose two decentralized equalizers for the star DBP architecture based on dimensionality reduction techniques. Then, we derive an optimal decentralized equalizer using the block coordinate descent (BCD) method for the daisy chain DBP architecture with a bandwidth reduction enhancement scheme based on decentralized low-rank decomposition. Finally, simulation results demonstrate that our proposed methods can achieve excellent detection performance while requiring much less communication bandwidth.

Low-Complexity Channel Estimation for Massive MIMO Systems with Decentralized Baseband Processing

The traditional centralized baseband processing architecture is faced with the bottlenecks of high computation complexity and excessive fronthaul communication, especially when the number of antennas at the base station (BS) is large. To cope with these two challenges, the decentralized baseband processing (DPB) architecture has been proposed, where the BS antennas are partitioned into multiple clusters, and each is connected to a local baseband unit (BBU). In this paper, we are interested in the low-complexity distributed channel estimation (CE) method under such DBP architecture, which is rarely studied in the literature. The aim is to devise distributed CE algorithms that can perform as well as the centralized scheme but with a small inter-BBU communication cost. Specifically, based on the low-complexity diagonal minimum mean square error channel estimator, we propose two distributed CE algorithms, namely the aggregate-then-estimate algorithm and the estimate-then-aggregate algorithm. In contrast to the existing distributed CE algorithm which requires iterative information exchanges among the nodes, our algorithms only require one roundtrip communication among BBUs. Extensive experiment results are presented to demonstrate the advantages of the proposed distributed CE algorithms in terms of estimation accuracy, inter-BBU communication cost, and computation complexity.

A sparse semismooth Newton based augmented Lagrangian method for large-scale support vector machines

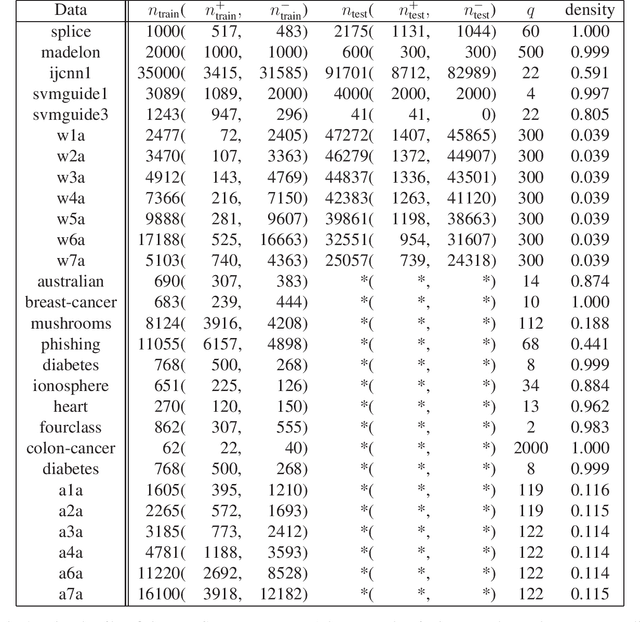
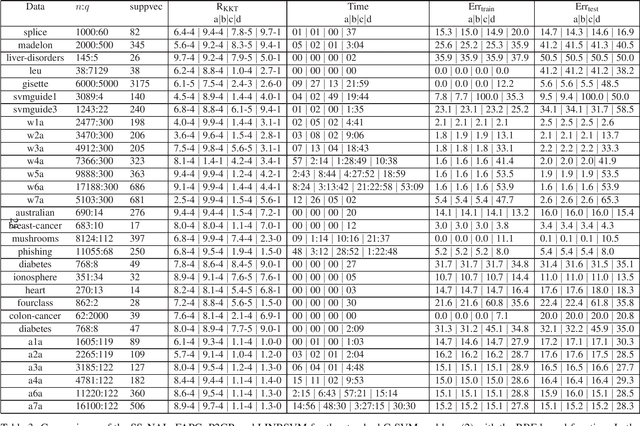
Support vector machines (SVMs) are successful modeling and prediction tools with a variety of applications. Previous work has demonstrated the superiority of the SVMs in dealing with the high dimensional, low sample size problems. However, the numerical difficulties of the SVMs will become severe with the increase of the sample size. Although there exist many solvers for the SVMs, only few of them are designed by exploiting the special structures of the SVMs. In this paper, we propose a highly efficient sparse semismooth Newton based augmented Lagrangian method for solving a large-scale convex quadratic programming problem with a linear equality constraint and a simple box constraint, which is generated from the dual problems of the SVMs. By leveraging the primal-dual error bound result, the fast local convergence rate of the augmented Lagrangian method can be guaranteed. Furthermore, by exploiting the second-order sparsity of the problem when using the semismooth Newton method, the algorithm can efficiently solve the aforementioned difficult problems. Finally, numerical comparisons demonstrate that the proposed algorithm outperforms the current state-of-the-art solvers for the large-scale SVMs.