Decentralized Equalization for Massive MIMO Systems With Colored Noise Samples

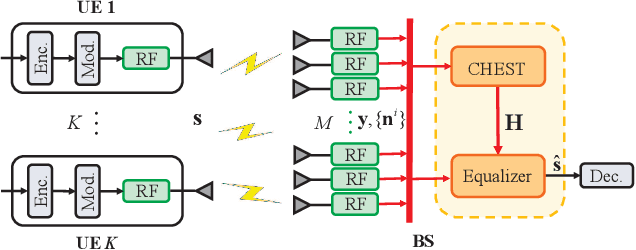
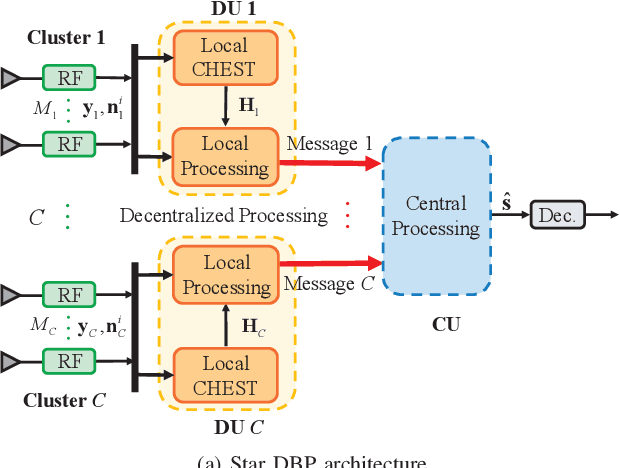
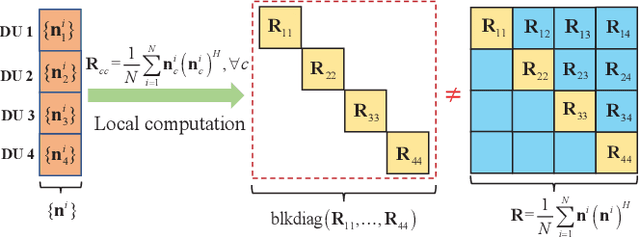
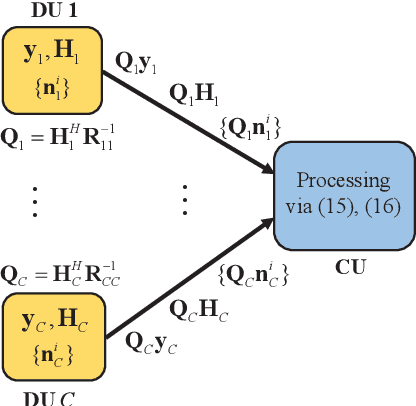
Recently, the decentralized baseband processing (DBP) paradigm and relevant detection methods have been proposed to enable extremely large-scale massive multiple-input multiple-output technology. Under the DBP architecture, base station antennas are divided into several independent clusters, each connected to a local computing fabric. However, current detection methods tailored to DBP only consider ideal white Gaussian noise scenarios, while in practice, the noise is often colored due to interference from neighboring cells. Moreover, in the DBP architecture, linear minimum mean-square error (LMMSE) detection methods rely on the estimation of the noise covariance matrix through averaging distributedly stored noise samples. This presents a significant challenge for decentralized LMMSE-based equalizer design. To address this issue, this paper proposes decentralized LMMSE equalization methods under colored noise scenarios for both star and daisy chain DBP architectures. Specifically, we first propose two decentralized equalizers for the star DBP architecture based on dimensionality reduction techniques. Then, we derive an optimal decentralized equalizer using the block coordinate descent (BCD) method for the daisy chain DBP architecture with a bandwidth reduction enhancement scheme based on decentralized low-rank decomposition. Finally, simulation results demonstrate that our proposed methods can achieve excellent detection performance while requiring much less communication bandwidth.