Chunfeng Cui
An Accelerated Alternating Partial Bregman Algorithm for ReLU-based Matrix Decomposition
Mar 04, 2025
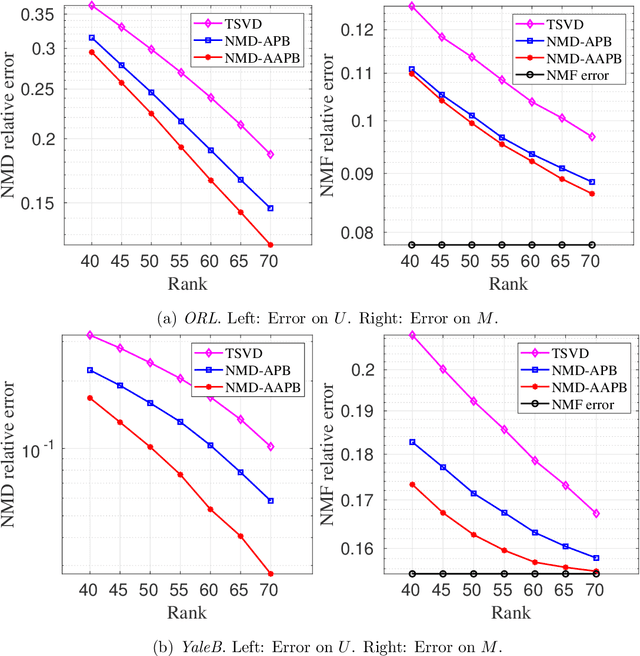


Abstract:Despite the remarkable success of low-rank estimation in data mining, its effectiveness diminishes when applied to data that inherently lacks low-rank structure. To address this limitation, in this paper, we focus on non-negative sparse matrices and aim to investigate the intrinsic low-rank characteristics of the rectified linear unit (ReLU) activation function. We first propose a novel nonlinear matrix decomposition framework incorporating a comprehensive regularization term designed to simultaneously promote useful structures in clustering and compression tasks, such as low-rankness, sparsity, and non-negativity in the resulting factors. This formulation presents significant computational challenges due to its multi-block structure, non-convexity, non-smoothness, and the absence of global gradient Lipschitz continuity. To address these challenges, we develop an accelerated alternating partial Bregman proximal gradient method (AAPB), whose distinctive feature lies in its capability to enable simultaneous updates of multiple variables. Under mild and theoretically justified assumptions, we establish both sublinear and global convergence properties of the proposed algorithm. Through careful selection of kernel generating distances tailored to various regularization terms, we derive corresponding closed-form solutions while maintaining the $L$-smooth adaptable property always holds for any $L\ge 1$. Numerical experiments, on graph regularized clustering and sparse NMF basis compression confirm the effectiveness of our model and algorithm.
Non-convex Pose Graph Optimization in SLAM via Proximal Linearized Riemannian ADMM
Apr 29, 2024Abstract:Pose graph optimization (PGO) is a well-known technique for solving the pose-based simultaneous localization and mapping (SLAM) problem. In this paper, we represent the rotation and translation by a unit quaternion and a three-dimensional vector, and propose a new PGO model based on the von Mises-Fisher distribution. The constraints derived from the unit quaternions are spherical manifolds, and the projection onto the constraints can be calculated by normalization. Then a proximal linearized Riemannian alternating direction method of multipliers (PieADMM) is developed to solve the proposed model, which not only has low memory requirements, but also can update the poses in parallel. Furthermore, we establish the iteration complexity of $O(1/\epsilon^{2})$ of PieADMM for finding an $\epsilon$-stationary solution of our model. The efficiency of our proposed algorithm is demonstrated by numerical experiments on two synthetic and four 3D SLAM benchmark datasets.
Pseudo MIMO : An Energy and Spectral Efficient MIMO-OFDM System
Apr 09, 2024



Abstract:This article introduces an energy and spectral efficient multiple-input multiple-output orthogonal frequency division multiplexing (MIMO-OFDM) transmission scheme designed for the future sixth generation (6G) wireless communication networks. The approach involves connecting each receiving radio frequency (RF) chain with multiple antenna elements and conducting sample-level adjustments for receiving beamforming patterns. The proposed system architecture and the dedicated signal processing methods enable the scheme to transmit a bigger number of parallel data streams than the number of receiving RF chains, achieving a spectral efficiency performance close to that of a fully digital (FD) MIMO system with the same number of antenna elements, each equipped with an RF chain. We refer to this system as a ''pseudo MIMO'' system due to its ability to mimic the functionality of additional invisible RF chains. The article begins with introducing the underlying principles of pseudo MIMO and discussing potential hardware architectures for its implementation. We then highlight several advantages of integrating pseudo MIMO into next-generation wireless networks. To demonstrate the superiority of our proposed pseudo MIMO transmission scheme to conventional MIMO systems, simulation results are presented. Additionally, we validate the feasibility of this new scheme by building the first pseudo MIMO prototype. Furthermore, we present some key challenges and outline potential directions for future research.
A Momentum Accelerated Algorithm for ReLU-based Nonlinear Matrix Decomposition
Feb 04, 2024Abstract:Recently, there has been a growing interest in the exploration of Nonlinear Matrix Decomposition (NMD) due to its close ties with neural networks. NMD aims to find a low-rank matrix from a sparse nonnegative matrix with a per-element nonlinear function. A typical choice is the Rectified Linear Unit (ReLU) activation function. To address over-fitting in the existing ReLU-based NMD model (ReLU-NMD), we propose a Tikhonov regularized ReLU-NMD model, referred to as ReLU-NMD-T. Subsequently, we introduce a momentum accelerated algorithm for handling the ReLU-NMD-T model. A distinctive feature, setting our work apart from most existing studies, is the incorporation of both positive and negative momentum parameters in our algorithm. Our numerical experiments on real-world datasets show the effectiveness of the proposed model and algorithm. Moreover, the code is available at https://github.com/nothing2wang/NMD-TM.
A Power Method for Computing the Dominant Eigenvalue of a Dual Quaternion Hermitian Matrix
May 01, 2023Abstract:In this paper, we first study the projections onto the set of unit dual quaternions, and the set of dual quaternion vectors with unit norms. Then we propose a power method for computing the dominant eigenvalue of a dual quaternion Hermitian matrix. For a strict dominant eigenvalue, we show the sequence generated by the power method converges to the dominant eigenvalue and its corresponding eigenvector linearly. For a general dominant eigenvalue, we show the standard part of the sequence generated by the power method converges to the standard part of the dominant eigenvalue and its corresponding eigenvector linearly. Based upon these, we reformulate the simultaneous localization and mapping (SLAM) problem as a rank-one dual quaternion completion problem. A two-block coordinate descent method is proposed to solve this problem. One block has a closed-form solution and the other block is the best rank-one approximation problem of a dual quaternion Hermitian matrix, which can be computed by the power method. Numerical experiments are presented to show the efficiency of our proposed power method.
Optimization Models and Interpretations for Three Types of Adversarial Perturbations against Support Vector Machines
Apr 07, 2022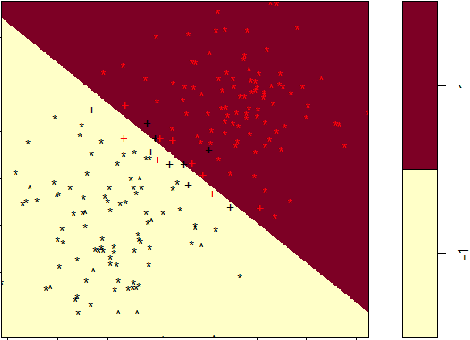



Abstract:Adversarial perturbations have drawn great attentions in various deep neural networks. Most of them are computed by iterations and cannot be interpreted very well. In contrast, little attentions are paid to basic machine learning models such as support vector machines. In this paper, we investigate the optimization models and the interpretations for three types of adversarial perturbations against support vector machines, including sample-adversarial perturbations (sAP), class-universal adversarial perturbations (cuAP) as well as universal adversarial perturbations (uAP). For linear binary/multi classification support vector machines (SVMs), we derive the explicit solutions for sAP, cuAP and uAP (binary case), and approximate solution for uAP of multi-classification. We also obtain the upper bound of fooling rate for uAP. Such results not only increase the interpretability of the three adversarial perturbations, but also provide great convenience in computation since iterative process can be avoided. Numerical results show that our method is fast and effective in calculating three types of adversarial perturbations.
Active Subspace of Neural Networks: Structural Analysis and Universal Attacks
Oct 29, 2019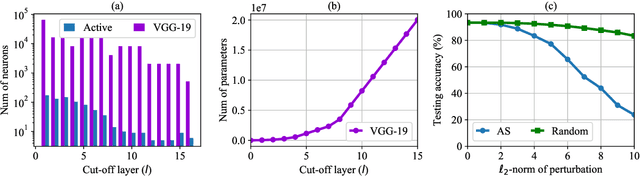
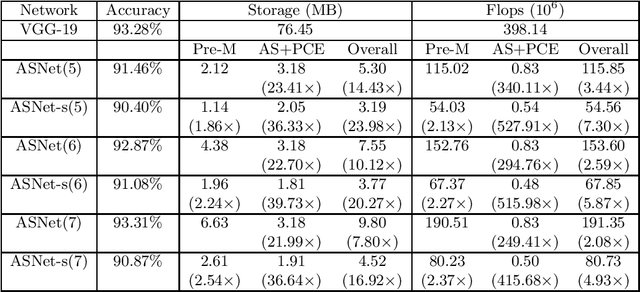
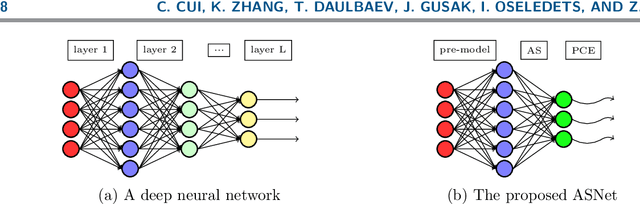
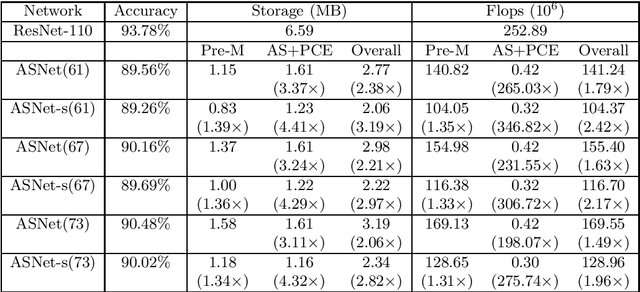
Abstract:Active subspace is a model reduction method widely used in the uncertainty quantification community. In this paper, we propose analyzing the internal structure and vulnerability and deep neural networks using active subspace. Firstly, we employ the active subspace to measure the number of "active neurons" at each intermediate layer and reduce the number of neurons from several thousands to several dozens. This motivates us to change the network structure and to develop a new and more compact network, referred to as {ASNet}, that has significantly fewer model parameters. Secondly, we propose analyzing the vulnerability of a neural network using active subspace and finding an additive universal adversarial attack vector that can misclassify a dataset with a high probability. Our experiments on CIFAR-10 show that ASNet can achieve 23.98$\times$ parameter and 7.30$\times$ flops reduction. The universal active subspace attack vector can achieve around 20% higher attack ratio compared with the existing approach in all of our numerical experiments. The PyTorch codes for this paper are available online.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge