Non-convex Pose Graph Optimization in SLAM via Proximal Linearized Riemannian ADMM

Pose graph optimization (PGO) is a well-known technique for solving the pose-based simultaneous localization and mapping (SLAM) problem. In this paper, we represent the rotation and translation by a unit quaternion and a three-dimensional vector, and propose a new PGO model based on the von Mises-Fisher distribution. The constraints derived from the unit quaternions are spherical manifolds, and the projection onto the constraints can be calculated by normalization. Then a proximal linearized Riemannian alternating direction method of multipliers (PieADMM) is developed to solve the proposed model, which not only has low memory requirements, but also can update the poses in parallel. Furthermore, we establish the iteration complexity of $O(1/\epsilon^{2})$ of PieADMM for finding an $\epsilon$-stationary solution of our model. The efficiency of our proposed algorithm is demonstrated by numerical experiments on two synthetic and four 3D SLAM benchmark datasets.

A Power Method for Computing the Dominant Eigenvalue of a Dual Quaternion Hermitian Matrix

In this paper, we first study the projections onto the set of unit dual quaternions, and the set of dual quaternion vectors with unit norms. Then we propose a power method for computing the dominant eigenvalue of a dual quaternion Hermitian matrix. For a strict dominant eigenvalue, we show the sequence generated by the power method converges to the dominant eigenvalue and its corresponding eigenvector linearly. For a general dominant eigenvalue, we show the standard part of the sequence generated by the power method converges to the standard part of the dominant eigenvalue and its corresponding eigenvector linearly. Based upon these, we reformulate the simultaneous localization and mapping (SLAM) problem as a rank-one dual quaternion completion problem. A two-block coordinate descent method is proposed to solve this problem. One block has a closed-form solution and the other block is the best rank-one approximation problem of a dual quaternion Hermitian matrix, which can be computed by the power method. Numerical experiments are presented to show the efficiency of our proposed power method.

Motion Addition and Motion Optimization

We introduce rotation addition and motion addition. In this way, motions replace unit dual quaternions to represent rigid body movements in the 3D space. The infinitesimal unit is no longer needed. By means of motion addition, we formulate two classical problems in robot research, i.e., the hand-eye calibration problem and the simultaneous localization and mapping (SLAM) problem as motion optimization problems, which are actually real unconstrained optimization problems. In particular, it avoids to go through the unit dual quaternion operations.

A regularization-patching dual quaternion optimization method for solving the hand-eye calibration problem

The hand-eye calibration problem is an important application problem in robot research. Based on the 2-norm of dual quaternion vectors, we propose a new dual quaternion optimization method for the hand-eye calibration problem. The dual quaternion optimization problem is decomposed to two quaternion optimization subproblems. The first quaternion optimization subproblem governs the rotation of the robot hand. It can be solved efficiently by the eigenvalue decomposition or singular value decomposition. If the optimal value of the first quaternion optimization subproblem is zero, then the system is rotationwise noiseless, i.e., there exists a ``perfect'' robot hand motion which meets all the testing poses rotationwise exactly. In this case, we apply the regularization technique for solving the second subproblem to minimize the distance of the translation. Otherwise we apply the patching technique to solve the second quaternion optimization subproblem. Then solving the second quaternion optimization subproblem turns out to be solving a quadratically constrained quadratic program. In this way, we give a complete description for the solution set of hand-eye calibration problems. This is new in the hand-eye calibration literature. The numerical results are also presented to show the efficiency of the proposed method.

Multi-mode Tensor Train Factorization with Spatial-spectral Regularization for Remote Sensing Images Recovery

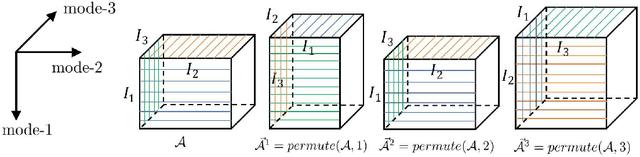
Tensor train (TT) factorization and corresponding TT rank, which can well express the low-rankness and mode correlations of higher-order tensors, have attracted much attention in recent years. However, TT factorization based methods are generally not sufficient to characterize low-rankness along each mode of third-order tensor. Inspired by this, we generalize the tensor train factorization to the mode-k tensor train factorization and introduce a corresponding multi-mode tensor train (MTT) rank. Then, we proposed a novel low-MTT-rank tensor completion model via multi-mode TT factorization and spatial-spectral smoothness regularization. To tackle the proposed model, we develop an efficient proximal alternating minimization (PAM) algorithm. Extensive numerical experiment results on visual data demonstrate that the proposed MTTD3R method outperforms compared methods in terms of visual and quantitative measures.

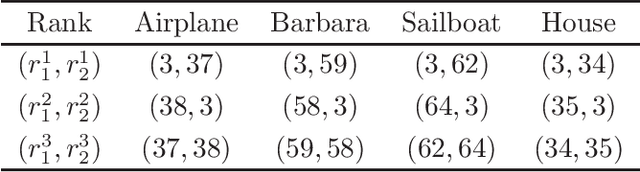
A DCT-based Tensor Completion Approach for Recovering Color Images and Videos from Highly Undersampled Data

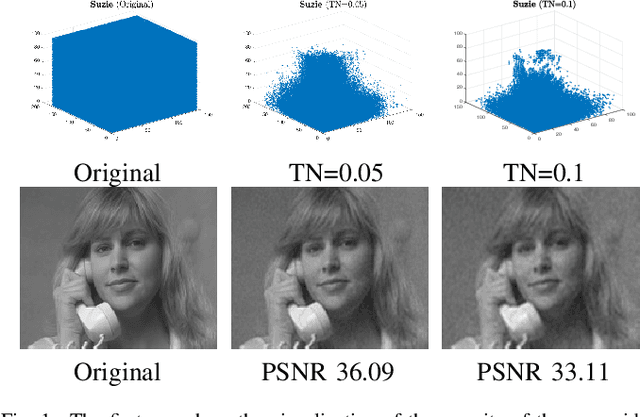
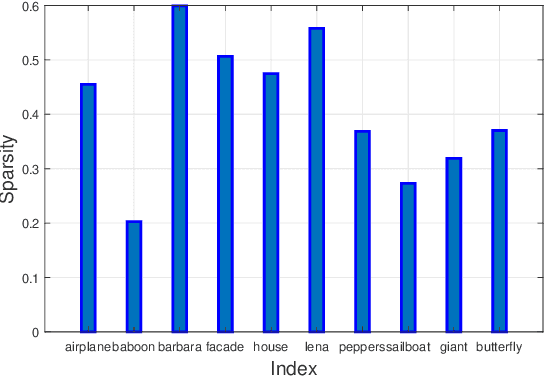
Recovering color images and videos from highly undersampled data is a fundamental and challenging task in face recognition and computer vision. By the multi-dimensional nature of color images and videos, in this paper, we propose a novel tensor completion approach, which is able to efficiently explore the sparsity of tensor data under the discrete cosine transform (DCT). Specifically, we introduce two DCT-based tensor completion models as well as two implementable algorithms for their solutions. The first one is a DCT-based weighted nuclear norm minimization model. The second one is called DCT-based $p$-shrinking tensor completion model, which is a nonconvex model utilizing $p$-shrinkage mapping for promoting the low-rankness of data. Moreover, we accordingly propose two implementable augmented Lagrangian-based algorithms for solving the underlying optimization models. A series of numerical experiments including color and MRI image inpainting and video data recovery demonstrate that our proposed approach performs better than many existing state-of-the-art tensor completion methods, especially for the case when the ratio of missing data is high.

Low-Rank and Sparse Enhanced Tucker Decomposition for Tensor Completion

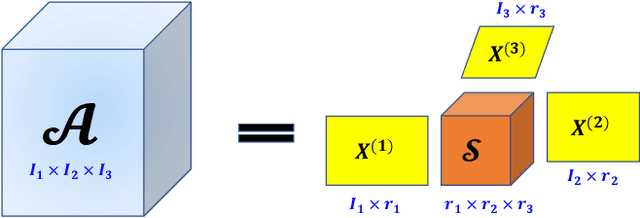
Tensor completion refers to the task of estimating the missing data from an incomplete measurement or observation, which is a core problem frequently arising from the areas of big data analysis, computer vision, and network engineering. Due to the multidimensional nature of high-order tensors, the matrix approaches, e.g., matrix factorization and direct matricization of tensors, are often not ideal for tensor completion and recovery. Exploiting the potential periodicity and inherent correlation properties appeared in real-world tensor data, in this paper, we shall incorporate the low-rank and sparse regularization technique to enhance Tucker decomposition for tensor completion. A series of computational experiments on real-world datasets, including internet traffic data, color images, and face recognition, show that our model performs better than many existing state-of-the-art matricization and tensorization approaches in terms of achieving higher recovery accuracy.