Structured model selection via $\ell_1-\ell_2$ optimization

Automated model selection is an important application in science and engineering. In this work, we develop a learning approach for identifying structured dynamical systems from undersampled and noisy spatiotemporal data. The learning is performed by a sparse least-squares fitting over a large set of candidate functions via a nonconvex $\ell_1-\ell_2$ sparse optimization solved by the alternating direction method of multipliers. Using a Bernstein-like inequality with a coherence condition, we show that if the set of candidate functions forms a structured random sampling matrix of a bounded orthogonal system, the recovery is stable and the error is bounded. The learning approach is validated on synthetic data generated by the viscous Burgers' equation and two reaction-diffusion equations. The computational results demonstrate the theoretical guarantees of success and the efficiency with respect to the ambient dimension and the number of candidate functions.

A DCT-based Tensor Completion Approach for Recovering Color Images and Videos from Highly Undersampled Data

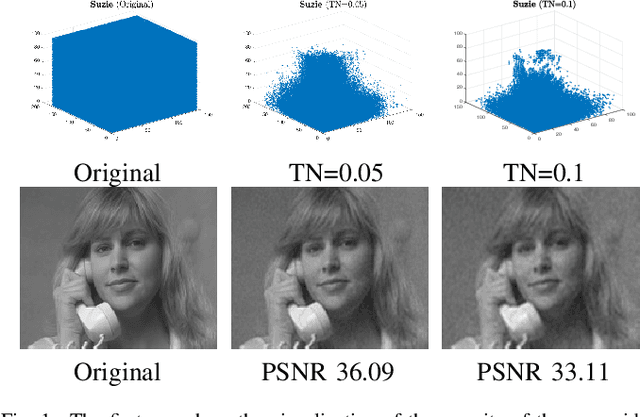
Recovering color images and videos from highly undersampled data is a fundamental and challenging task in face recognition and computer vision. By the multi-dimensional nature of color images and videos, in this paper, we propose a novel tensor completion approach, which is able to efficiently explore the sparsity of tensor data under the discrete cosine transform (DCT). Specifically, we introduce two DCT-based tensor completion models as well as two implementable algorithms for their solutions. The first one is a DCT-based weighted nuclear norm minimization model. The second one is called DCT-based $p$-shrinking tensor completion model, which is a nonconvex model utilizing $p$-shrinkage mapping for promoting the low-rankness of data. Moreover, we accordingly propose two implementable augmented Lagrangian-based algorithms for solving the underlying optimization models. A series of numerical experiments including color and MRI image inpainting and video data recovery demonstrate that our proposed approach performs better than many existing state-of-the-art tensor completion methods, especially for the case when the ratio of missing data is high.

Low-Rank and Sparse Enhanced Tucker Decomposition for Tensor Completion

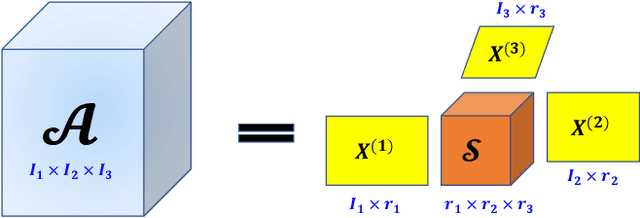
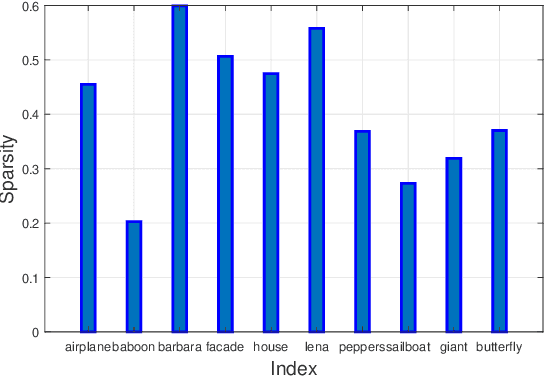
Tensor completion refers to the task of estimating the missing data from an incomplete measurement or observation, which is a core problem frequently arising from the areas of big data analysis, computer vision, and network engineering. Due to the multidimensional nature of high-order tensors, the matrix approaches, e.g., matrix factorization and direct matricization of tensors, are often not ideal for tensor completion and recovery. Exploiting the potential periodicity and inherent correlation properties appeared in real-world tensor data, in this paper, we shall incorporate the low-rank and sparse regularization technique to enhance Tucker decomposition for tensor completion. A series of computational experiments on real-world datasets, including internet traffic data, color images, and face recognition, show that our model performs better than many existing state-of-the-art matricization and tensorization approaches in terms of achieving higher recovery accuracy.