Deren Han
An Accelerated Alternating Partial Bregman Algorithm for ReLU-based Matrix Decomposition
Mar 04, 2025
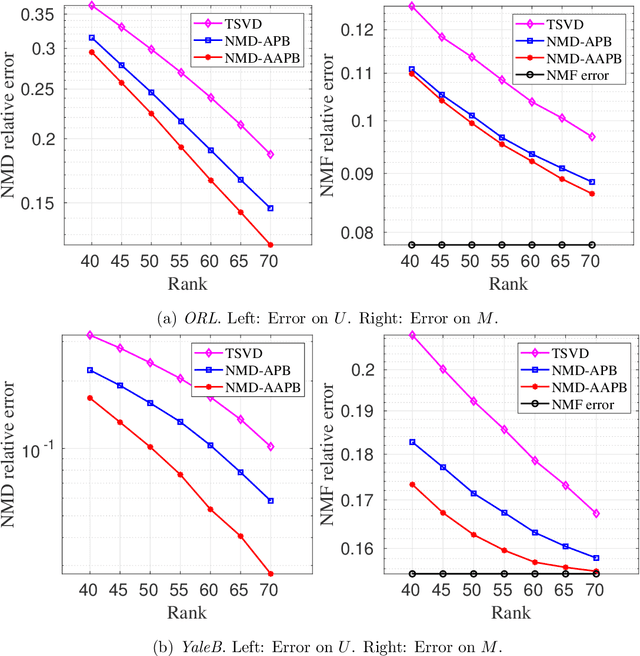


Abstract:Despite the remarkable success of low-rank estimation in data mining, its effectiveness diminishes when applied to data that inherently lacks low-rank structure. To address this limitation, in this paper, we focus on non-negative sparse matrices and aim to investigate the intrinsic low-rank characteristics of the rectified linear unit (ReLU) activation function. We first propose a novel nonlinear matrix decomposition framework incorporating a comprehensive regularization term designed to simultaneously promote useful structures in clustering and compression tasks, such as low-rankness, sparsity, and non-negativity in the resulting factors. This formulation presents significant computational challenges due to its multi-block structure, non-convexity, non-smoothness, and the absence of global gradient Lipschitz continuity. To address these challenges, we develop an accelerated alternating partial Bregman proximal gradient method (AAPB), whose distinctive feature lies in its capability to enable simultaneous updates of multiple variables. Under mild and theoretically justified assumptions, we establish both sublinear and global convergence properties of the proposed algorithm. Through careful selection of kernel generating distances tailored to various regularization terms, we derive corresponding closed-form solutions while maintaining the $L$-smooth adaptable property always holds for any $L\ge 1$. Numerical experiments, on graph regularized clustering and sparse NMF basis compression confirm the effectiveness of our model and algorithm.
Fair Primal Dual Splitting Method for Image Inverse Problems
Dec 11, 2024Abstract:Image inverse problems have numerous applications, including image processing, super-resolution, and computer vision, which are important areas in image science. These application models can be seen as a three-function composite optimization problem solvable by a variety of primal dual-type methods. We propose a fair primal dual algorithmic framework that incorporates the smooth term not only into the primal subproblem but also into the dual subproblem. We unify the global convergence and establish the convergence rates of our proposed fair primal dual method. Experiments on image denoising and super-resolution reconstruction demonstrate the superiority of the proposed method over the current state-of-the-art.
Novel clustered federated learning based on local loss
Jul 12, 2024Abstract:This paper proposes LCFL, a novel clustering metric for evaluating clients' data distributions in federated learning. LCFL aligns with federated learning requirements, accurately assessing client-to-client variations in data distribution. It offers advantages over existing clustered federated learning methods, addressing privacy concerns, improving applicability to non-convex models, and providing more accurate classification results. LCFL does not require prior knowledge of clients' data distributions. We provide a rigorous mathematical analysis, demonstrating the correctness and feasibility of our framework. Numerical experiments with neural network instances highlight the superior performance of LCFL over baselines on several clustered federated learning benchmarks.
Non-convex Pose Graph Optimization in SLAM via Proximal Linearized Riemannian ADMM
Apr 29, 2024Abstract:Pose graph optimization (PGO) is a well-known technique for solving the pose-based simultaneous localization and mapping (SLAM) problem. In this paper, we represent the rotation and translation by a unit quaternion and a three-dimensional vector, and propose a new PGO model based on the von Mises-Fisher distribution. The constraints derived from the unit quaternions are spherical manifolds, and the projection onto the constraints can be calculated by normalization. Then a proximal linearized Riemannian alternating direction method of multipliers (PieADMM) is developed to solve the proposed model, which not only has low memory requirements, but also can update the poses in parallel. Furthermore, we establish the iteration complexity of $O(1/\epsilon^{2})$ of PieADMM for finding an $\epsilon$-stationary solution of our model. The efficiency of our proposed algorithm is demonstrated by numerical experiments on two synthetic and four 3D SLAM benchmark datasets.
A Momentum Accelerated Algorithm for ReLU-based Nonlinear Matrix Decomposition
Feb 04, 2024Abstract:Recently, there has been a growing interest in the exploration of Nonlinear Matrix Decomposition (NMD) due to its close ties with neural networks. NMD aims to find a low-rank matrix from a sparse nonnegative matrix with a per-element nonlinear function. A typical choice is the Rectified Linear Unit (ReLU) activation function. To address over-fitting in the existing ReLU-based NMD model (ReLU-NMD), we propose a Tikhonov regularized ReLU-NMD model, referred to as ReLU-NMD-T. Subsequently, we introduce a momentum accelerated algorithm for handling the ReLU-NMD-T model. A distinctive feature, setting our work apart from most existing studies, is the incorporation of both positive and negative momentum parameters in our algorithm. Our numerical experiments on real-world datasets show the effectiveness of the proposed model and algorithm. Moreover, the code is available at https://github.com/nothing2wang/NMD-TM.
The neural network models with delays for solving absolute value equations
Oct 17, 2023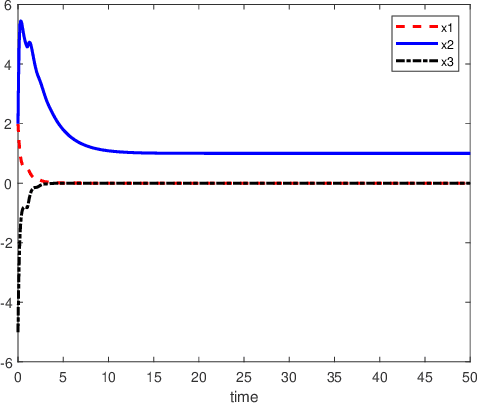
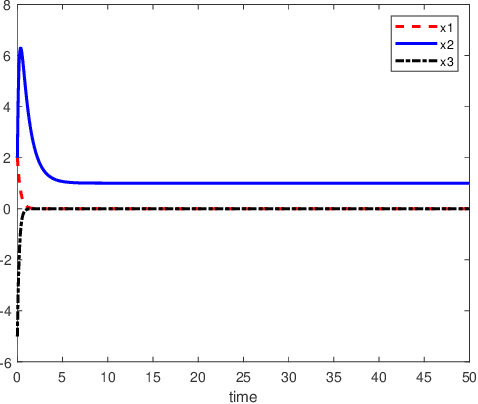
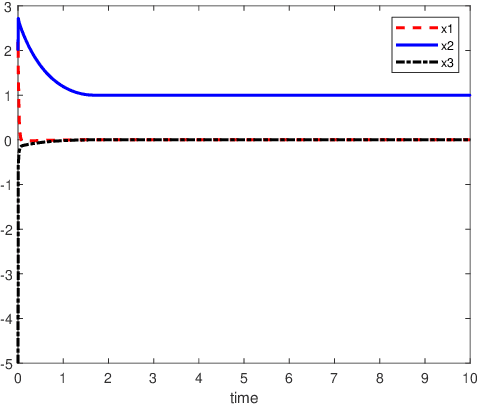
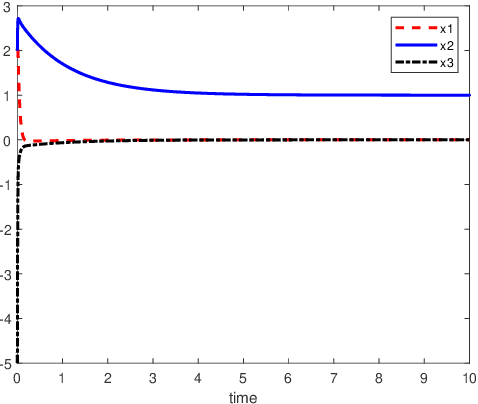
Abstract:An inverse-free neural network model with mixed delays is proposed for solving the absolute value equation (AVE) $Ax -|x| - b =0$, which includes an inverse-free neural network model with discrete delay as a special case. By using the Lyapunov-Krasovskii theory and the linear matrix inequality (LMI) method, the developed neural network models are proved to be exponentially convergent to the solution of the AVE. Compared with the existing neural network models for solving the AVE, the proposed models feature the ability of solving a class of AVE with $\|A^{-1}\|>1$. Numerical simulations are given to show the effectiveness of the two delayed neural network models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge