The neural network models with delays for solving absolute value equations
Paper and Code
Oct 17, 2023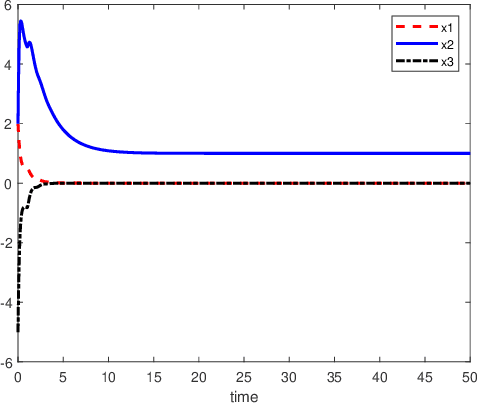
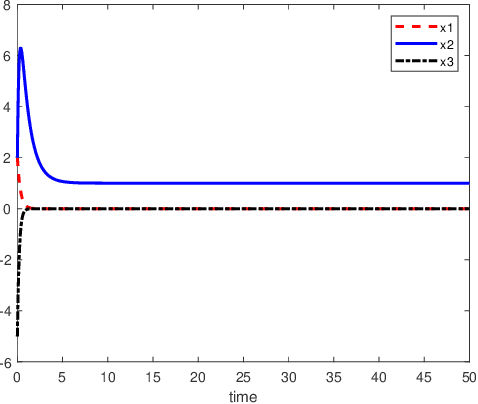
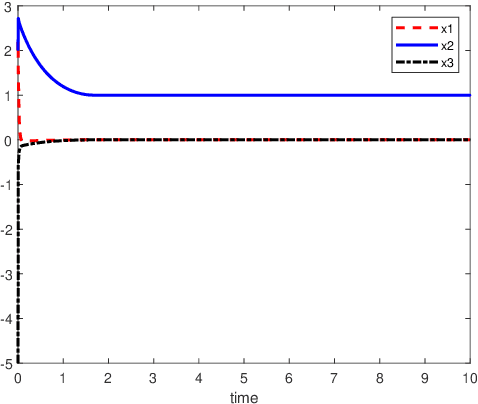
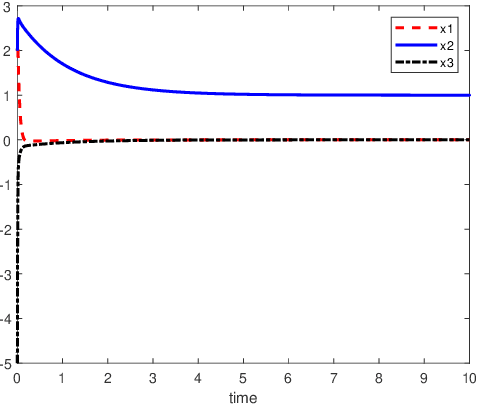
An inverse-free neural network model with mixed delays is proposed for solving the absolute value equation (AVE) $Ax -|x| - b =0$, which includes an inverse-free neural network model with discrete delay as a special case. By using the Lyapunov-Krasovskii theory and the linear matrix inequality (LMI) method, the developed neural network models are proved to be exponentially convergent to the solution of the AVE. Compared with the existing neural network models for solving the AVE, the proposed models feature the ability of solving a class of AVE with $\|A^{-1}\|>1$. Numerical simulations are given to show the effectiveness of the two delayed neural network models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge