Gaohang Yu
tCURLoRA: Tensor CUR Decomposition Based Low-Rank Parameter Adaptation for Medical Image Segmentation
Jan 04, 2025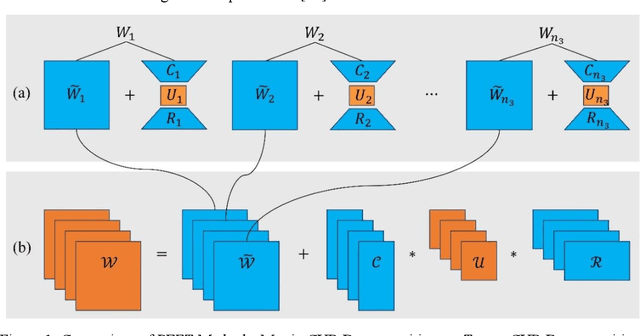

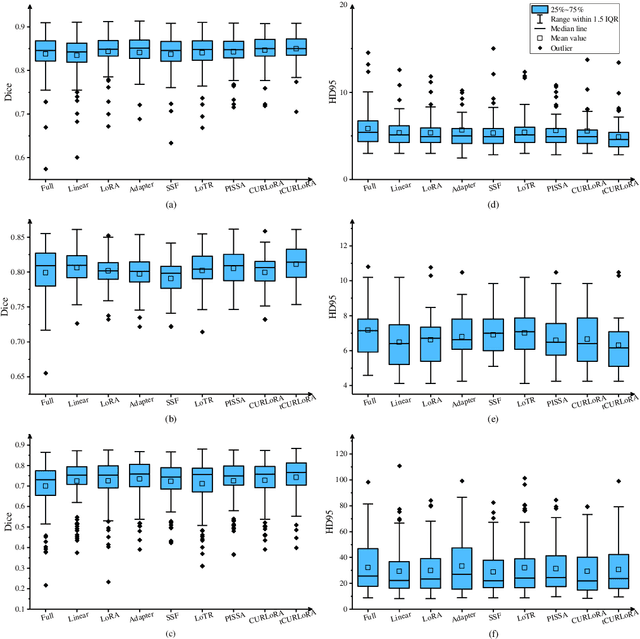
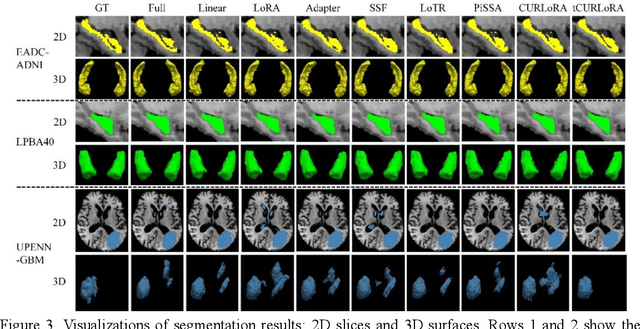
Abstract:Transfer learning, by leveraging knowledge from pre-trained models, has significantly enhanced the performance of target tasks. However, as deep neural networks scale up, full fine-tuning introduces substantial computational and storage challenges in resource-constrained environments, limiting its widespread adoption. To address this, parameter-efficient fine-tuning (PEFT) methods have been developed to reduce computational complexity and storage requirements by minimizing the number of updated parameters. While matrix decomposition-based PEFT methods, such as LoRA, show promise, they struggle to fully capture the high-dimensional structural characteristics of model weights. In contrast, high-dimensional tensors offer a more natural representation of neural network weights, allowing for a more comprehensive capture of higher-order features and multi-dimensional interactions. In this paper, we propose tCURLoRA, a novel fine-tuning method based on tensor CUR decomposition. By concatenating pre-trained weight matrices into a three-dimensional tensor and applying tensor CUR decomposition, we update only the lower-order tensor components during fine-tuning, effectively reducing computational and storage overhead. Experimental results demonstrate that tCURLoRA outperforms existing PEFT methods in medical image segmentation tasks.
LoRA-PT: Low-Rank Adapting UNETR for Hippocampus Segmentation Using Principal Tensor Singular Values and Vectors
Jul 16, 2024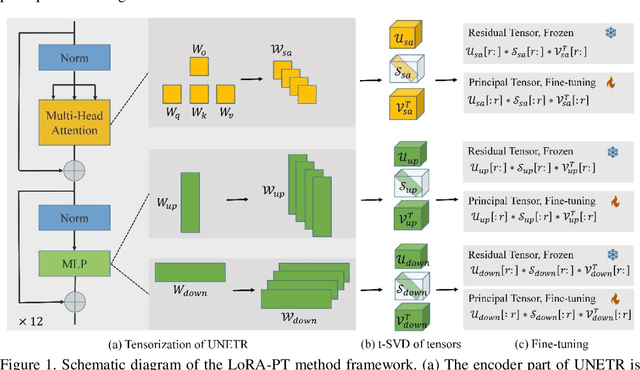

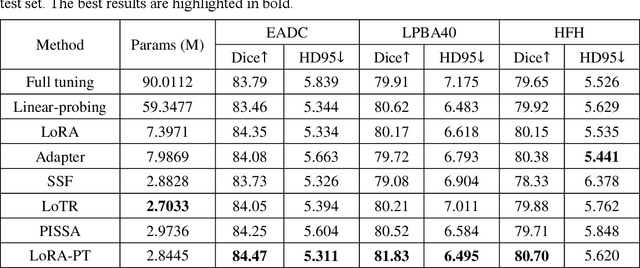
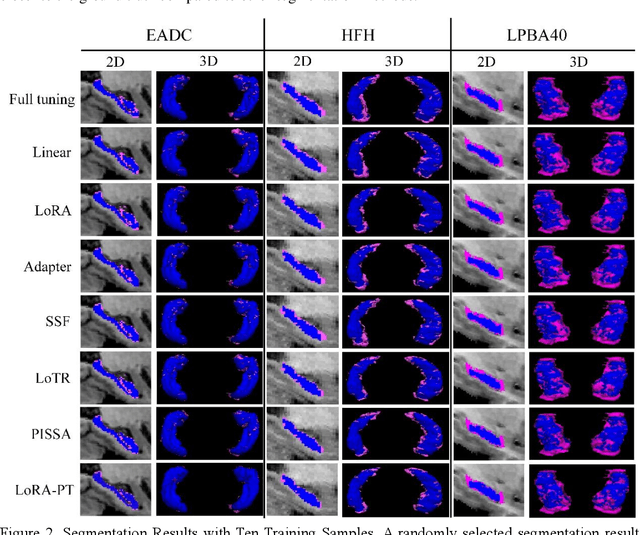
Abstract:The hippocampus is a crucial brain structure associated with various psychiatric disorders, and its automatic and precise segmentation is essential for studying these diseases. In recent years, deep learning-based methods have made significant progress in hippocampus segmentation. However, training deep neural network models requires substantial computational resources and time, as well as a large amount of labeled training data, which is often difficult to obtain in medical image segmentation. To address this issue, we propose a new parameter-efficient fine-tuning method called LoRA-PT. This method transfers the pre-trained UNETR model on the BraTS2021 dataset to the hippocampus segmentation task. Specifically, the LoRA-PT method categorizes the parameter matrix of the transformer structure into three sizes, forming three 3D tensors. Through tensor singular value decomposition, these tensors are decomposed to generate low-rank tensors with the principal singular values and singular vectors, while the remaining singular values and vectors form the residual tensor. Similar to the LoRA method, during parameter fine-tuning, we only update the low-rank tensors, i.e. the principal tensor singular values and vectors, while keeping the residual tensor unchanged. We validated the proposed method on three public hippocampus datasets. Experimental results show that LoRA-PT outperforms existing parameter-efficient transfer learning methods in segmentation accuracy while significantly reducing the number of parameter updates.
Multi-mode Tensor Train Factorization with Spatial-spectral Regularization for Remote Sensing Images Recovery
May 05, 2022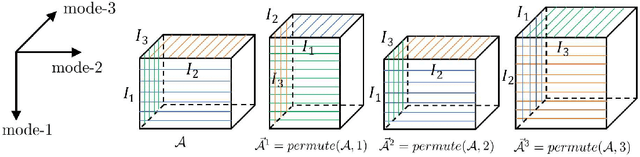


Abstract:Tensor train (TT) factorization and corresponding TT rank, which can well express the low-rankness and mode correlations of higher-order tensors, have attracted much attention in recent years. However, TT factorization based methods are generally not sufficient to characterize low-rankness along each mode of third-order tensor. Inspired by this, we generalize the tensor train factorization to the mode-k tensor train factorization and introduce a corresponding multi-mode tensor train (MTT) rank. Then, we proposed a novel low-MTT-rank tensor completion model via multi-mode TT factorization and spatial-spectral smoothness regularization. To tackle the proposed model, we develop an efficient proximal alternating minimization (PAM) algorithm. Extensive numerical experiment results on visual data demonstrate that the proposed MTTD3R method outperforms compared methods in terms of visual and quantitative measures.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge