Qingna Li
An Efficient Method for Sample Adversarial Perturbations against Nonlinear Support Vector Machines
Jun 12, 2022



Abstract:Adversarial perturbations have drawn great attentions in various machine learning models. In this paper, we investigate the sample adversarial perturbations for nonlinear support vector machines (SVMs). Due to the implicit form of the nonlinear functions mapping data to the feature space, it is difficult to obtain the explicit form of the adversarial perturbations. By exploring the special property of nonlinear SVMs, we transform the optimization problem of attacking nonlinear SVMs into a nonlinear KKT system. Such a system can be solved by various numerical methods. Numerical results show that our method is efficient in computing adversarial perturbations.
Optimization Models and Interpretations for Three Types of Adversarial Perturbations against Support Vector Machines
Apr 07, 2022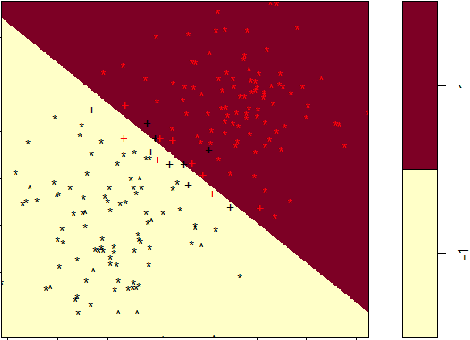



Abstract:Adversarial perturbations have drawn great attentions in various deep neural networks. Most of them are computed by iterations and cannot be interpreted very well. In contrast, little attentions are paid to basic machine learning models such as support vector machines. In this paper, we investigate the optimization models and the interpretations for three types of adversarial perturbations against support vector machines, including sample-adversarial perturbations (sAP), class-universal adversarial perturbations (cuAP) as well as universal adversarial perturbations (uAP). For linear binary/multi classification support vector machines (SVMs), we derive the explicit solutions for sAP, cuAP and uAP (binary case), and approximate solution for uAP of multi-classification. We also obtain the upper bound of fooling rate for uAP. Such results not only increase the interpretability of the three adversarial perturbations, but also provide great convenience in computation since iterative process can be avoided. Numerical results show that our method is fast and effective in calculating three types of adversarial perturbations.
A Semismooth-Newton's-Method-Based Linearization and Approximation Approach for Kernel Support Vector Machines
Jul 21, 2020



Abstract:Support Vector Machines (SVMs) are among the most popular and the best performing classification algorithms. Various approaches have been proposed to reduce the high computation and memory cost when training and predicting based on large-scale datasets with kernel SVMs. A popular one is the linearization framework, which successfully builds a bridge between the $L_1$-loss kernel SVM and the $L_1$-loss linear SVM. For linear SVMs, very recently, a semismooth Newton's method is proposed. It is shown to be very competitive and have low computational cost. Consequently, a natural question is whether it is possible to develop a fast semismooth Newton's algorithm for kernel SVMs. Motivated by this question and the idea in linearization framework, in this paper, we focus on the $L_2$-loss kernel SVM and propose a semismooth Newton's method based linearization and approximation approach for it. The main idea of this approach is to first set up an equivalent linear SVM, then apply the Nystr\"om method to approximate the kernel matrix, based on which a reduced linear SVM is obtained. Finally, the fast semismooth Newton's method is employed to solve the reduced linear SVM. We also provide some theoretical analyses on the approximation of the kernel matrix. The advantage of the proposed approach is that it maintains low computational cost and keeps a fast convergence rate. Results of extensive numerical experiments verify the efficiency of the proposed approach in terms of both predicting accuracy and speed.
Ordinal Distance Metric Learning with MDS for Image Ranking
Feb 27, 2019



Abstract:Image ranking is to rank images based on some known ranked images. In this paper, we propose an improved linear ordinal distance metric learning approach based on the linear distance metric learning model. By decomposing the distance metric $A$ as $L^TL$, the problem can be cast as looking for a linear map between two sets of points in different spaces, meanwhile maintaining some data structures. The ordinal relation of the labels can be maintained via classical multidimensional scaling, a popular tool for dimension reduction in statistics. A least squares fitting term is then introduced to the cost function, which can also maintain the local data structure. The resulting model is an unconstrained problem, and can better fit the data structure. Extensive numerical results demonstrate the improvement of the new approach over the linear distance metric learning model both in speed and ranking performance.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge