MSSDF: Modality-Shared Self-supervised Distillation for High-Resolution Multi-modal Remote Sensing Image Learning

Remote sensing image interpretation plays a critical role in environmental monitoring, urban planning, and disaster assessment. However, acquiring high-quality labeled data is often costly and time-consuming. To address this challenge, we proposes a multi-modal self-supervised learning framework that leverages high-resolution RGB images, multi-spectral data, and digital surface models (DSM) for pre-training. By designing an information-aware adaptive masking strategy, cross-modal masking mechanism, and multi-task self-supervised objectives, the framework effectively captures both the correlations across different modalities and the unique feature structures within each modality. We evaluated the proposed method on multiple downstream tasks, covering typical remote sensing applications such as scene classification, semantic segmentation, change detection, object detection, and depth estimation. Experiments are conducted on 15 remote sensing datasets, encompassing 26 tasks. The results demonstrate that the proposed method outperforms existing pretraining approaches in most tasks. Specifically, on the Potsdam and Vaihingen semantic segmentation tasks, our method achieved mIoU scores of 78.30\% and 76.50\%, with only 50\% train-set. For the US3D depth estimation task, the RMSE error is reduced to 0.182, and for the binary change detection task in SECOND dataset, our method achieved mIoU scores of 47.51\%, surpassing the second CS-MAE by 3 percentage points. Our pretrain code, checkpoints, and HR-Pairs dataset can be found in https://github.com/CVEO/MSSDF.

MSV-Mamba: A Multiscale Vision Mamba Network for Echocardiography Segmentation

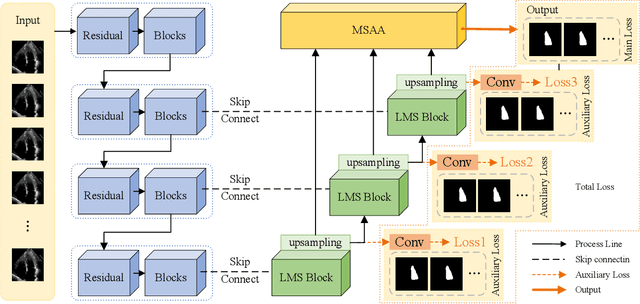
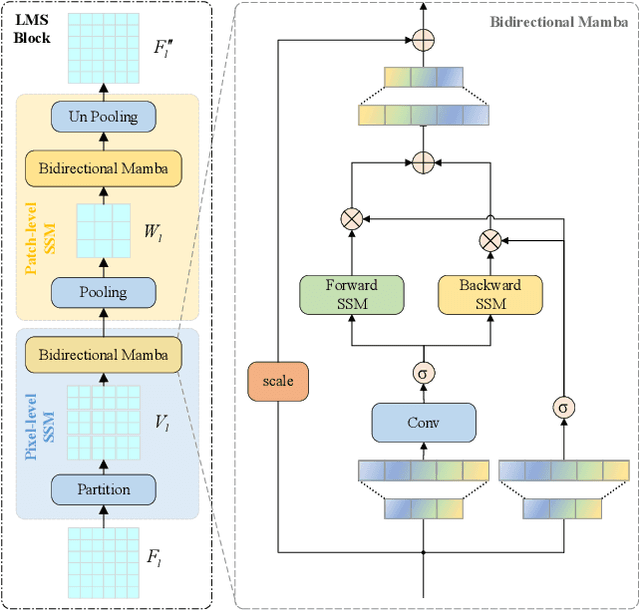
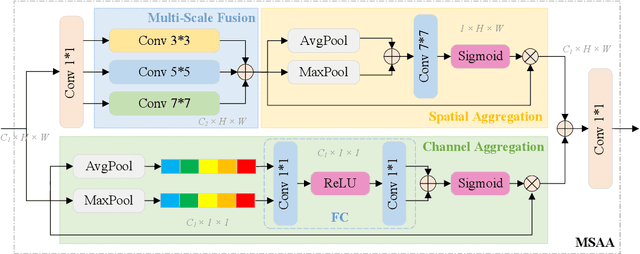
Ultrasound imaging frequently encounters challenges, such as those related to elevated noise levels, diminished spatiotemporal resolution, and the complexity of anatomical structures. These factors significantly hinder the model's ability to accurately capture and analyze structural relationships and dynamic patterns across various regions of the heart. Mamba, an emerging model, is one of the most cutting-edge approaches that is widely applied to diverse vision and language tasks. To this end, this paper introduces a U-shaped deep learning model incorporating a large-window Mamba scale (LMS) module and a hierarchical feature fusion approach for echocardiographic segmentation. First, a cascaded residual block serves as an encoder and is employed to incrementally extract multiscale detailed features. Second, a large-window multiscale mamba module is integrated into the decoder to capture global dependencies across regions and enhance the segmentation capability for complex anatomical structures. Furthermore, our model introduces auxiliary losses at each decoder layer and employs a dual attention mechanism to fuse multilayer features both spatially and across channels. This approach enhances segmentation performance and accuracy in delineating complex anatomical structures. Finally, the experimental results using the EchoNet-Dynamic and CAMUS datasets demonstrate that the model outperforms other methods in terms of both accuracy and robustness. For the segmentation of the left ventricular endocardium (${LV}_{endo}$), the model achieved optimal values of 95.01 and 93.36, respectively, while for the left ventricular epicardium (${LV}_{epi}$), values of 87.35 and 87.80, respectively, were achieved. This represents an improvement ranging between 0.54 and 1.11 compared with the best-performing model.

KOALA: Enhancing Speculative Decoding for LLM via Multi-Layer Draft Heads with Adversarial Learning

Large Language Models (LLMs) exhibit high inference latency due to their autoregressive decoding nature. While the draft head in speculative decoding mitigates this issue, its full potential remains unexplored. In this paper, we introduce KOALA (K-layer Optimized Adversarial Learning Architecture), an orthogonal approach to the draft head. By transforming the conventional single-layer draft head into a multi-layer architecture and incorporating adversarial learning into the traditional supervised training, KOALA significantly improves the accuracy of the draft head in predicting subsequent tokens, thus more closely mirroring the functionality of LLMs. Although this improvement comes at the cost of slightly increased drafting overhead, KOALA substantially unlocks the draft head's potential, greatly enhancing speculative decoding. We conducted comprehensive evaluations of KOALA, including both autoregressive and non-autoregressive draft heads across various tasks, demonstrating a latency speedup ratio improvement of 0.24x-0.41x, which is 10.57%-14.09% faster than the original draft heads.

Stable Minima Cannot Overfit in Univariate ReLU Networks: Generalization by Large Step Sizes

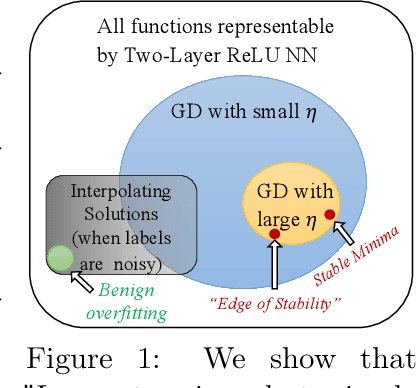
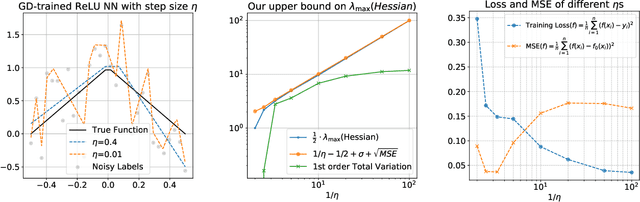
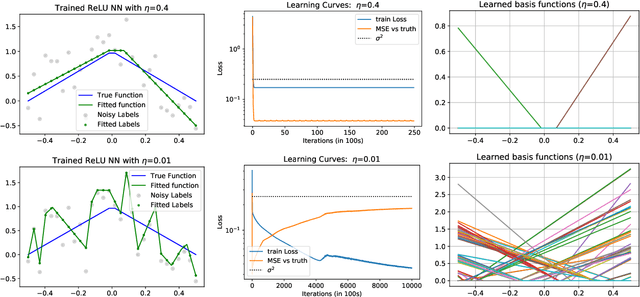
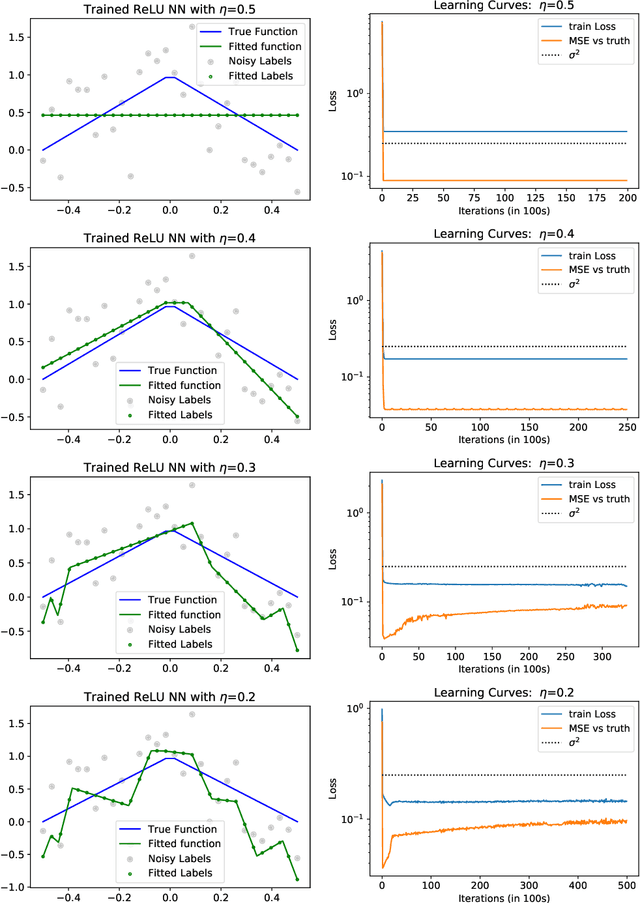
We study the generalization of two-layer ReLU neural networks in a univariate nonparametric regression problem with noisy labels. This is a problem where kernels (\emph{e.g.} NTK) are provably sub-optimal and benign overfitting does not happen, thus disqualifying existing theory for interpolating (0-loss, global optimal) solutions. We present a new theory of generalization for local minima that gradient descent with a constant learning rate can \emph{stably} converge to. We show that gradient descent with a fixed learning rate $\eta$ can only find local minima that represent smooth functions with a certain weighted \emph{first order total variation} bounded by $1/\eta - 1/2 + \widetilde{O}(\sigma + \sqrt{\mathrm{MSE}})$ where $\sigma$ is the label noise level, $\mathrm{MSE}$ is short for mean squared error against the ground truth, and $\widetilde{O}(\cdot)$ hides a logarithmic factor. Under mild assumptions, we also prove a nearly-optimal MSE bound of $\widetilde{O}(n^{-4/5})$ within the strict interior of the support of the $n$ data points. Our theoretical results are validated by extensive simulation that demonstrates large learning rate training induces sparse linear spline fits. To the best of our knowledge, we are the first to obtain generalization bound via minima stability in the non-interpolation case and the first to show ReLU NNs without regularization can achieve near-optimal rates in nonparametric regression.

Nonparametric Classification on Low Dimensional Manifolds using Overparameterized Convolutional Residual Networks

Convolutional residual neural networks (ConvResNets), though overparameterized, can achieve remarkable prediction performance in practice, which cannot be well explained by conventional wisdom. To bridge this gap, we study the performance of ConvResNeXts, which cover ConvResNets as a special case, trained with weight decay from the perspective of nonparametric classification. Our analysis allows for infinitely many building blocks in ConvResNeXts, and shows that weight decay implicitly enforces sparsity on these blocks. Specifically, we consider a smooth target function supported on a low-dimensional manifold, then prove that ConvResNeXts can adapt to the function smoothness and low-dimensional structures and efficiently learn the function without suffering from the curse of dimensionality. Our findings partially justify the advantage of overparameterized ConvResNeXts over conventional machine learning models.

Why Quantization Improves Generalization: NTK of Binary Weight Neural Networks

Quantized neural networks have drawn a lot of attention as they reduce the space and computational complexity during the inference. Moreover, there has been folklore that quantization acts as an implicit regularizer and thus can improve the generalizability of neural networks, yet no existing work formalizes this interesting folklore. In this paper, we take the binary weights in a neural network as random variables under stochastic rounding, and study the distribution propagation over different layers in the neural network. We propose a quasi neural network to approximate the distribution propagation, which is a neural network with continuous parameters and smooth activation function. We derive the neural tangent kernel (NTK) for this quasi neural network, and show that the eigenvalue of NTK decays at approximately exponential rate, which is comparable to that of Gaussian kernel with randomized scale. This in turn indicates that the Reproducing Kernel Hilbert Space (RKHS) of a binary weight neural network covers a strict subset of functions compared with the one with real value weights. We use experiments to verify that the quasi neural network we proposed can well approximate binary weight neural network. Furthermore, binary weight neural network gives a lower generalization gap compared with real value weight neural network, which is similar to the difference between Gaussian kernel and Laplace kernel.

Deep Learning meets Nonparametric Regression: Are Weight-Decayed DNNs Locally Adaptive?

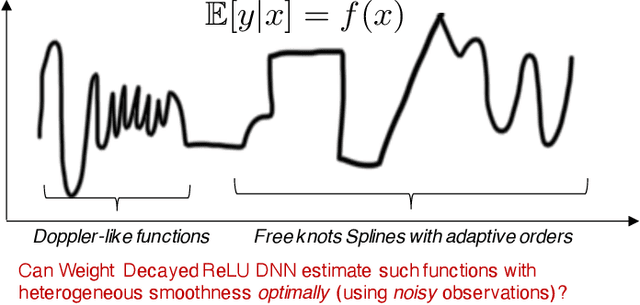
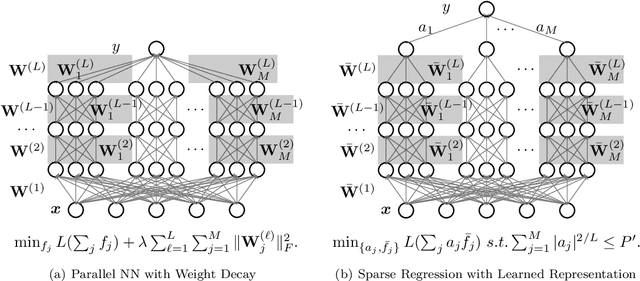
We study the theory of neural network (NN) from the lens of classical nonparametric regression problems with a focus on NN's ability to adaptively estimate functions with heterogeneous smoothness -- a property of functions in Besov or Bounded Variation (BV) classes. Existing work on this problem requires tuning the NN architecture based on the function spaces and sample sizes. We consider a "Parallel NN" variant of deep ReLU networks and show that the standard weight decay is equivalent to promoting the $\ell_p$-sparsity ($0<p<1$) of the coefficient vector of an end-to-end learned function bases, i.e., a dictionary. Using this equivalence, we further establish that by tuning only the weight decay, such Parallel NN achieves an estimation error arbitrarily close to the minimax rates for both the Besov and BV classes. Notably, it gets exponentially closer to minimax optimal as the NN gets deeper. Our research sheds new lights on why depth matters and how NNs are more powerful than kernel methods.

3U-EdgeAI: Ultra-Low Memory Training, Ultra-Low BitwidthQuantization, and Ultra-Low Latency Acceleration

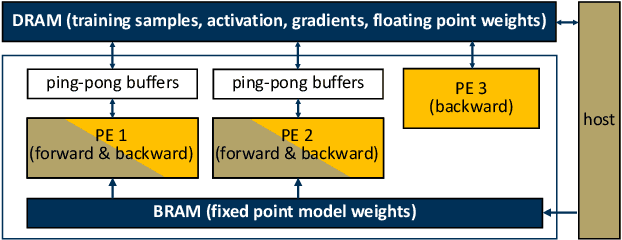
The deep neural network (DNN) based AI applications on the edge require both low-cost computing platforms and high-quality services. However, the limited memory, computing resources, and power budget of the edge devices constrain the effectiveness of the DNN algorithms. Developing edge-oriented AI algorithms and implementations (e.g., accelerators) is challenging. In this paper, we summarize our recent efforts for efficient on-device AI development from three aspects, including both training and inference. First, we present on-device training with ultra-low memory usage. We propose a novel rank-adaptive tensor-based tensorized neural network model, which offers orders-of-magnitude memory reduction during training. Second, we introduce an ultra-low bitwidth quantization method for DNN model compression, achieving the state-of-the-art accuracy under the same compression ratio. Third, we introduce an ultra-low latency DNN accelerator design, practicing the software/hardware co-design methodology. This paper emphasizes the importance and efficacy of training, quantization and accelerator design, and calls for more research breakthroughs in the area for AI on the edge.

Active Subspace of Neural Networks: Structural Analysis and Universal Attacks

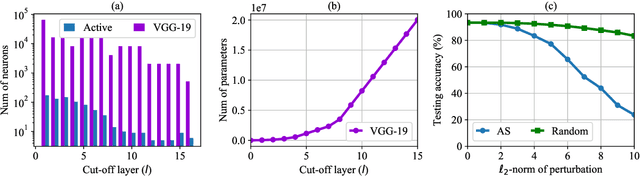
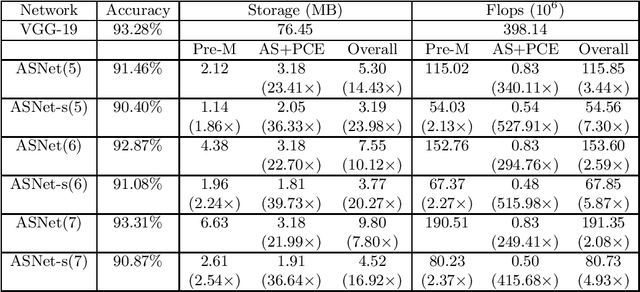
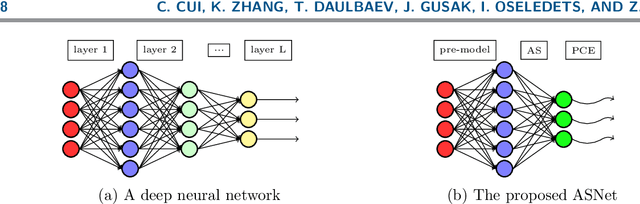
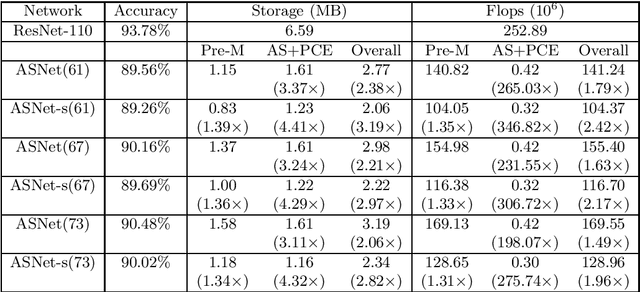
Active subspace is a model reduction method widely used in the uncertainty quantification community. In this paper, we propose analyzing the internal structure and vulnerability and deep neural networks using active subspace. Firstly, we employ the active subspace to measure the number of "active neurons" at each intermediate layer and reduce the number of neurons from several thousands to several dozens. This motivates us to change the network structure and to develop a new and more compact network, referred to as {ASNet}, that has significantly fewer model parameters. Secondly, we propose analyzing the vulnerability of a neural network using active subspace and finding an additive universal adversarial attack vector that can misclassify a dataset with a high probability. Our experiments on CIFAR-10 show that ASNet can achieve 23.98$\times$ parameter and 7.30$\times$ flops reduction. The universal active subspace attack vector can achieve around 20% higher attack ratio compared with the existing approach in all of our numerical experiments. The PyTorch codes for this paper are available online.

A Unified Framework of DNN Weight Pruning and Weight Clustering/Quantization Using ADMM

Many model compression techniques of Deep Neural Networks (DNNs) have been investigated, including weight pruning, weight clustering and quantization, etc. Weight pruning leverages the redundancy in the number of weights in DNNs, while weight clustering/quantization leverages the redundancy in the number of bit representations of weights. They can be effectively combined in order to exploit the maximum degree of redundancy. However, there lacks a systematic investigation in literature towards this direction. In this paper, we fill this void and develop a unified, systematic framework of DNN weight pruning and clustering/quantization using Alternating Direction Method of Multipliers (ADMM), a powerful technique in optimization theory to deal with non-convex optimization problems. Both DNN weight pruning and clustering/quantization, as well as their combinations, can be solved in a unified manner. For further performance improvement in this framework, we adopt multiple techniques including iterative weight quantization and retraining, joint weight clustering training and centroid updating, weight clustering retraining, etc. The proposed framework achieves significant improvements both in individual weight pruning and clustering/quantization problems, as well as their combinations. For weight pruning alone, we achieve 167x weight reduction in LeNet-5, 24.7x in AlexNet, and 23.4x in VGGNet, without any accuracy loss. For the combination of DNN weight pruning and clustering/quantization, we achieve 1,910x and 210x storage reduction of weight data on LeNet-5 and AlexNet, respectively, without accuracy loss. Our codes and models are released at the link http://bit.ly/2D3F0np