Efficient Long-Range Transformers: You Need to Attend More, but Not Necessarily at Every Layer

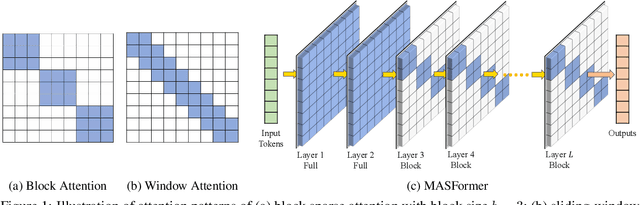
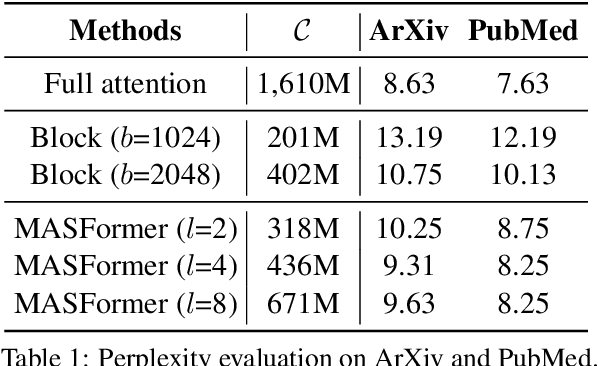
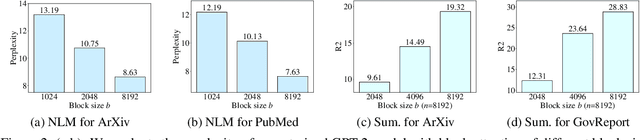
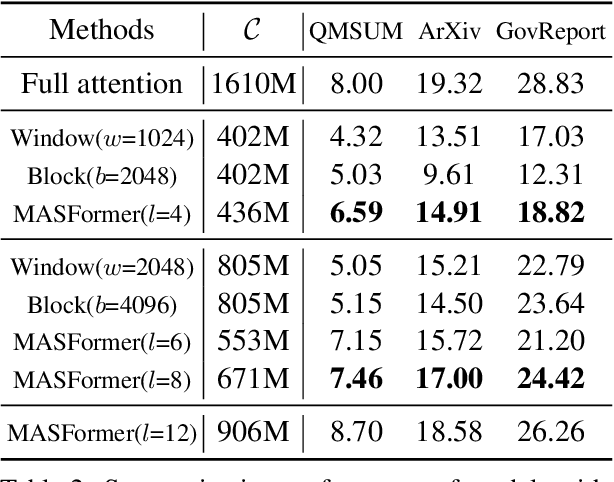
Pretrained transformer models have demonstrated remarkable performance across various natural language processing tasks. These models leverage the attention mechanism to capture long- and short-range dependencies in the sequence. However, the (full) attention mechanism incurs high computational cost - quadratic in the sequence length, which is not affordable in tasks with long sequences, e.g., inputs with 8k tokens. Although sparse attention can be used to improve computational efficiency, as suggested in existing work, it has limited modeling capacity and often fails to capture complicated dependencies in long sequences. To tackle this challenge, we propose MASFormer, an easy-to-implement transformer variant with Mixed Attention Spans. Specifically, MASFormer is equipped with full attention to capture long-range dependencies, but only at a small number of layers. For the remaining layers, MASformer only employs sparse attention to capture short-range dependencies. Our experiments on natural language modeling and generation tasks show that a decoder-only MASFormer model of 1.3B parameters can achieve competitive performance to vanilla transformers with full attention while significantly reducing computational cost (up to 75%). Additionally, we investigate the effectiveness of continual training with long sequence data and how sequence length impacts downstream generation performance, which may be of independent interest.

Vcc: Scaling Transformers to 128K Tokens or More by Prioritizing Important Tokens

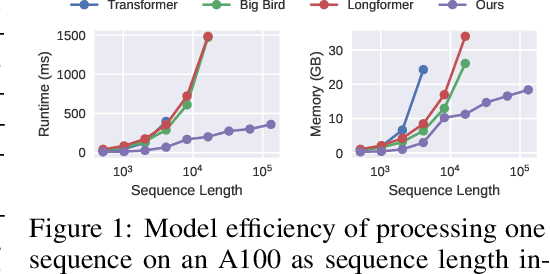
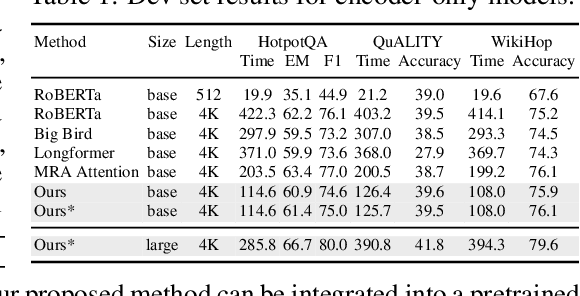
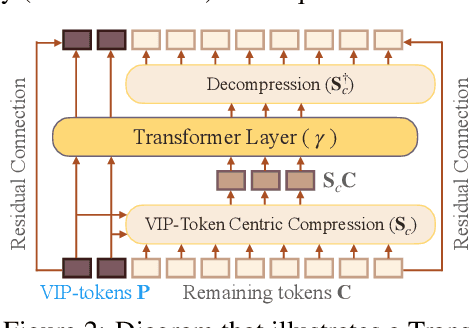
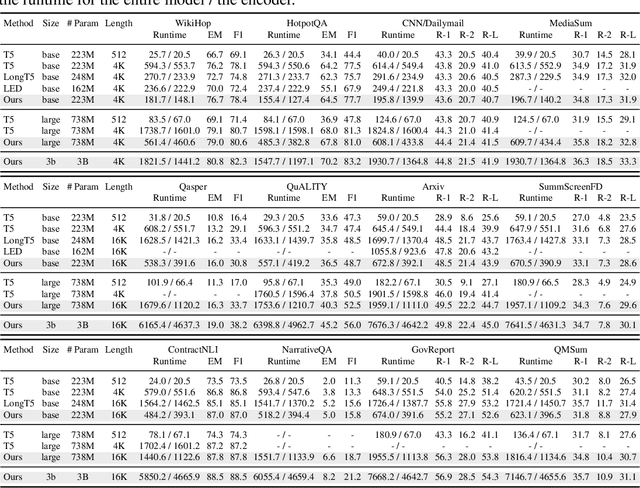
Transformer models are foundational to natural language processing (NLP) and computer vision. Despite various recent works devoted to reducing the quadratic cost of such models (as a function of the sequence length $n$), dealing with ultra long sequences efficiently (e.g., with more than 16K tokens) remains challenging. Applications such as answering questions based on an entire book or summarizing a scientific article are inefficient or infeasible. In this paper, we propose to significantly reduce the dependency of a Transformer model's complexity on $n$, by compressing the input into a representation whose size $r$ is independent of $n$ at each layer. Specifically, by exploiting the fact that in many tasks, only a small subset of special tokens (we call VIP-tokens) are most relevant to the final prediction, we propose a VIP-token centric compression (Vcc) scheme which selectively compresses the input sequence based on their impact on approximating the representation of these VIP-tokens. Compared with competitive baselines, the proposed algorithm not only is efficient (achieving more than $3\times$ efficiency improvement compared to baselines on 4K and 16K lengths), but also achieves competitive or better performance on a large number of tasks. Further, we show that our algorithm can be scaled to 128K tokens (or more) while consistently offering accuracy improvement.

Online, Informative MCMC Thinning with Kernelized Stein Discrepancy

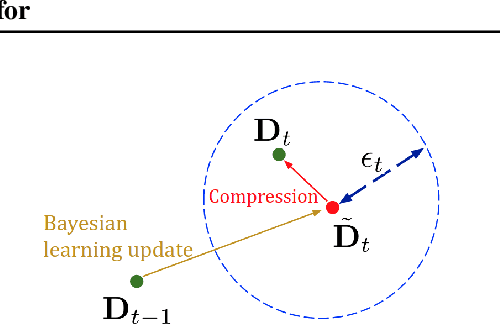
A fundamental challenge in Bayesian inference is efficient representation of a target distribution. Many non-parametric approaches do so by sampling a large number of points using variants of Markov Chain Monte Carlo (MCMC). We propose an MCMC variant that retains only those posterior samples which exceed a KSD threshold, which we call KSD Thinning. We establish the convergence and complexity tradeoffs for several settings of KSD Thinning as a function of the KSD threshold parameter, sample size, and other problem parameters. Finally, we provide experimental comparisons against other online nonparametric Bayesian methods that generate low-complexity posterior representations, and observe superior consistency/complexity tradeoffs. Code is available at github.com/colehawkins/KSD-Thinning.

Low-Rank+Sparse Tensor Compression for Neural Networks

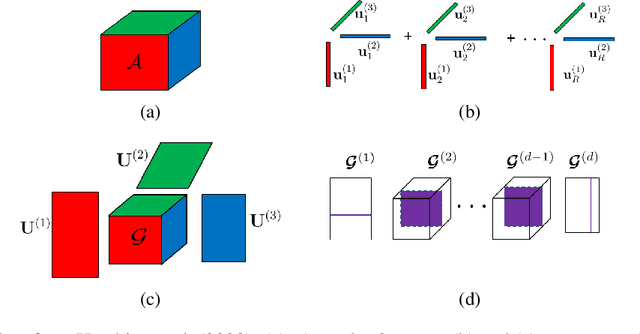
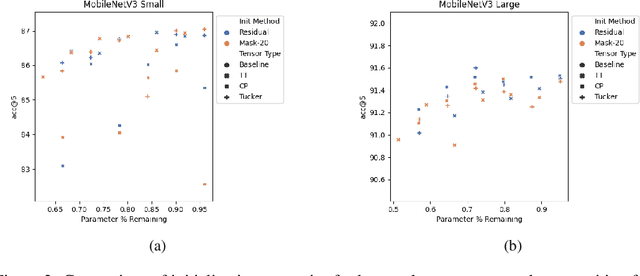
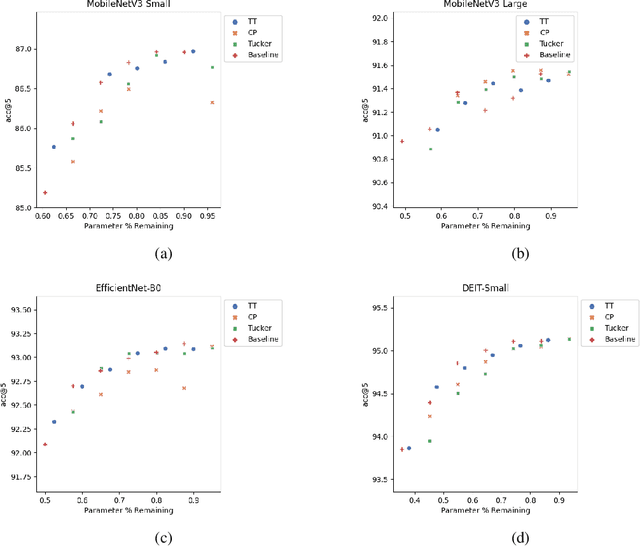
Low-rank tensor compression has been proposed as a promising approach to reduce the memory and compute requirements of neural networks for their deployment on edge devices. Tensor compression reduces the number of parameters required to represent a neural network weight by assuming network weights possess a coarse higher-order structure. This coarse structure assumption has been applied to compress large neural networks such as VGG and ResNet. However modern state-of-the-art neural networks for computer vision tasks (i.e. MobileNet, EfficientNet) already assume a coarse factorized structure through depthwise separable convolutions, making pure tensor decomposition a less attractive approach. We propose to combine low-rank tensor decomposition with sparse pruning in order to take advantage of both coarse and fine structure for compression. We compress weights in SOTA architectures (MobileNetv3, EfficientNet, Vision Transformer) and compare this approach to sparse pruning and tensor decomposition alone.

Scalable Consistency Training for Graph Neural Networks via Self-Ensemble Self-Distillation

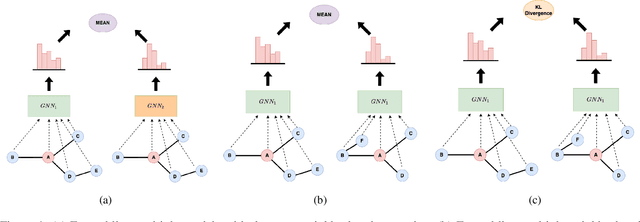
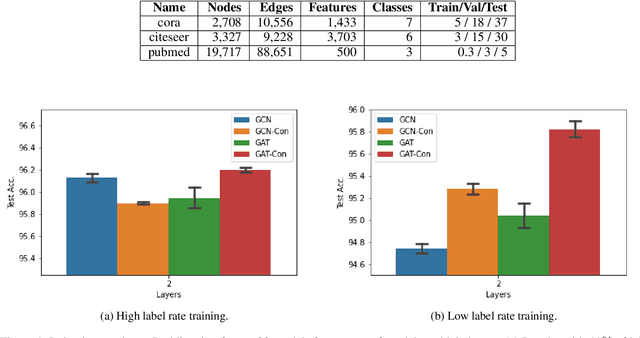
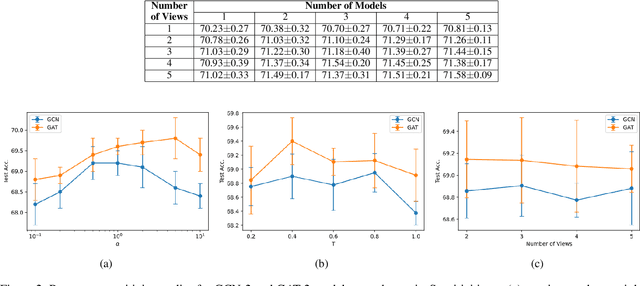
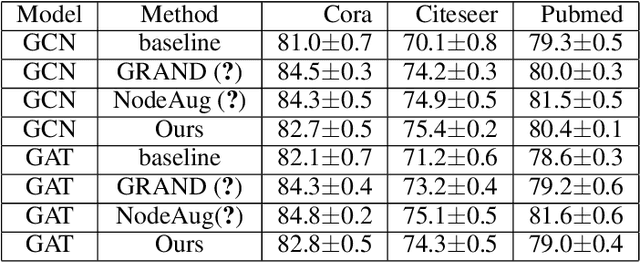
Consistency training is a popular method to improve deep learning models in computer vision and natural language processing. Graph neural networks (GNNs) have achieved remarkable performance in a variety of network science learning tasks, but to date no work has studied the effect of consistency training on large-scale graph problems. GNNs scale to large graphs by minibatch training and subsample node neighbors to deal with high degree nodes. We utilize the randomness inherent in the subsampling of neighbors and introduce a novel consistency training method to improve accuracy. For a target node we generate different neighborhood expansions, and distill the knowledge of the average of the predictions to the GNN. Our method approximates the expected prediction of the possible neighborhood samples and practically only requires a few samples. We demonstrate that our training method outperforms standard GNN training in several different settings, and yields the largest gains when label rates are low.

3U-EdgeAI: Ultra-Low Memory Training, Ultra-Low BitwidthQuantization, and Ultra-Low Latency Acceleration

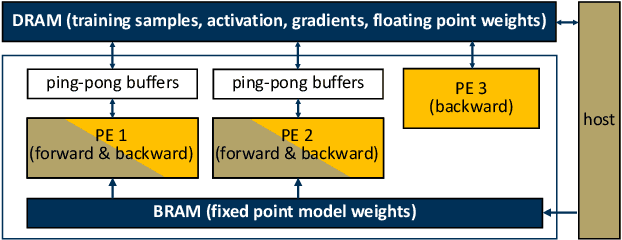
The deep neural network (DNN) based AI applications on the edge require both low-cost computing platforms and high-quality services. However, the limited memory, computing resources, and power budget of the edge devices constrain the effectiveness of the DNN algorithms. Developing edge-oriented AI algorithms and implementations (e.g., accelerators) is challenging. In this paper, we summarize our recent efforts for efficient on-device AI development from three aspects, including both training and inference. First, we present on-device training with ultra-low memory usage. We propose a novel rank-adaptive tensor-based tensorized neural network model, which offers orders-of-magnitude memory reduction during training. Second, we introduce an ultra-low bitwidth quantization method for DNN model compression, achieving the state-of-the-art accuracy under the same compression ratio. Third, we introduce an ultra-low latency DNN accelerator design, practicing the software/hardware co-design methodology. This paper emphasizes the importance and efficacy of training, quantization and accelerator design, and calls for more research breakthroughs in the area for AI on the edge.

End-to-End Variational Bayesian Training of Tensorized Neural Networks with Automatic Rank Determination

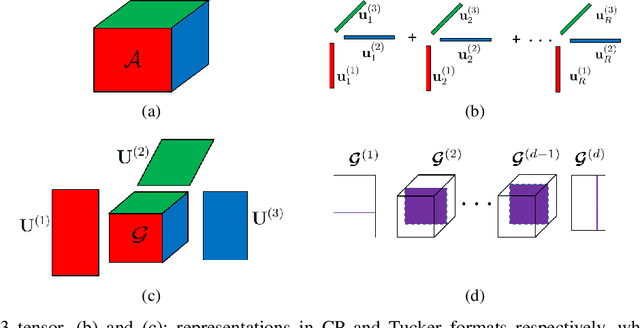
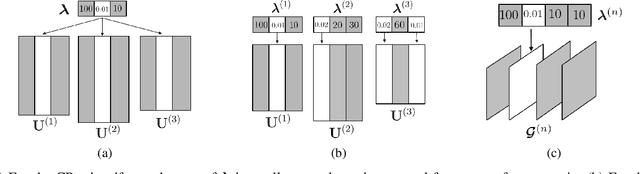
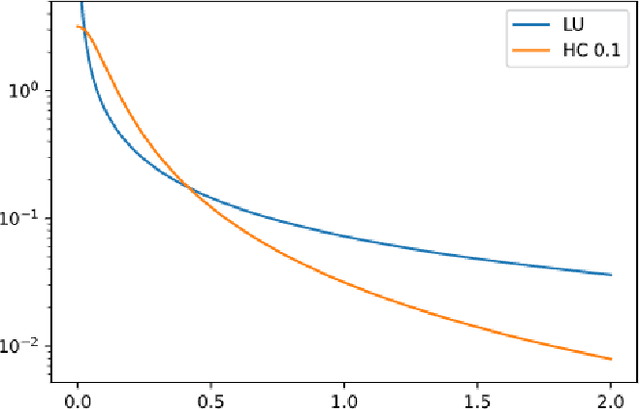
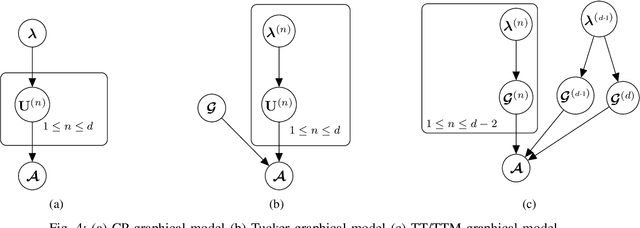
Low-rank tensor decomposition is one of the most effective approaches to reduce the memory and computing requirements of large-size neural networks, enabling their efficient deployment on various hardware platforms. While post-training tensor compression can greatly reduce the cost of inference, uncompressed training still consumes excessive hardware resources, run-time and energy. It is highly desirable to directly train a compact low-rank tensorized model from scratch with a low memory and computational cost. However, this is a very challenging task because it is hard to determine a proper tensor rank a priori, which controls the model complexity and compression ratio in the training process. This paper presents a novel end-to-end framework for low-rank tensorized training of neural networks. We first develop a flexible Bayesian model that can handle various low-rank tensor formats (e.g., CP, Tucker, tensor train and tensor-train matrix) that compress neural network parameters in training. This model can automatically determine the tensor ranks inside a nonlinear forward model, which is beyond the capability of existing Bayesian tensor methods. We further develop a scalable stochastic variational inference solver to estimate the posterior density of large-scale problems in training. Our work provides the first general-purpose rank-adaptive framework for end-to-end tensorized training. Our numerical results on various neural network architectures show orders-of-magnitude parameter reduction and little accuracy loss (or even better accuracy) in the training process.

Bayesian Tensorized Neural Networks with Automatic Rank Selection

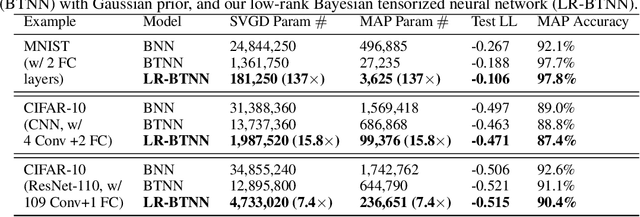
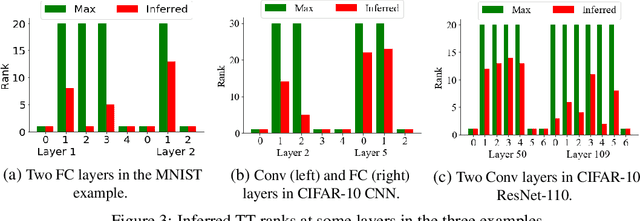
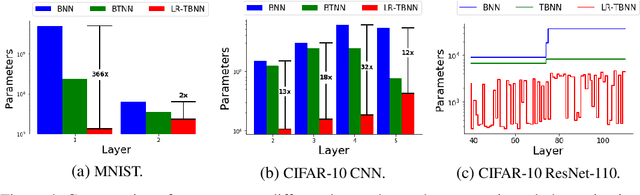
Tensor decomposition is an effective approach to compress over-parameterized neural networks and to enable their deployment on resource-constrained hardware platforms. However, directly applying tensor compression in the training process is a challenging task due to the difficulty of choosing a proper tensor rank. In order to achieve this goal, this paper proposes a Bayesian tensorized neural network. Our Bayesian method performs automatic model compression via an adaptive tensor rank determination. We also present approaches for posterior density calculation and maximum a posteriori (MAP) estimation for the end-to-end training of our tensorized neural network. We provide experimental validation on a fully connected neural network, a CNN and a residual neural network where our work produces $7.4\times$ to $137\times$ more compact neural networks directly from the training.

Variational Bayesian Inference for Robust Streaming Tensor Factorization and Completion

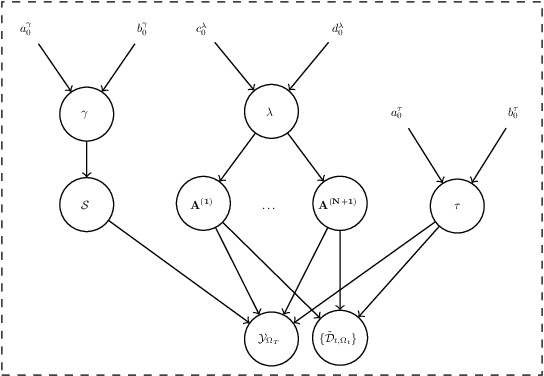
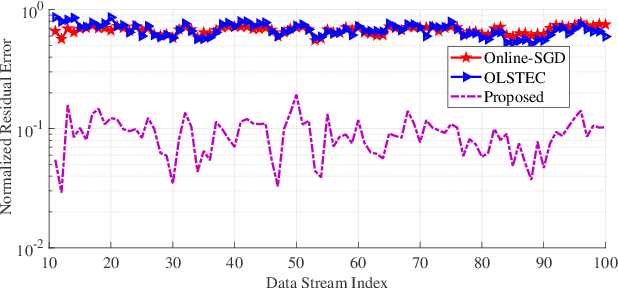
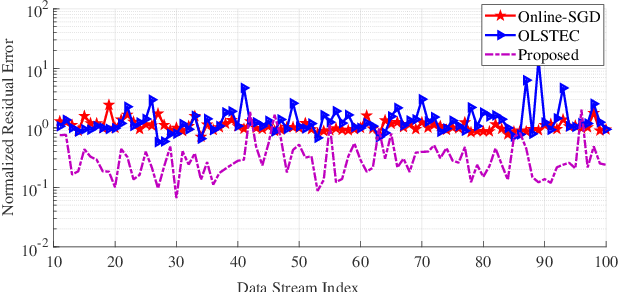
Streaming tensor factorization is a powerful tool for processing high-volume and multi-way temporal data in Internet networks, recommender systems and image/video data analysis. Existing streaming tensor factorization algorithms rely on least-squares data fitting and they do not possess a mechanism for tensor rank determination. This leaves them susceptible to outliers and vulnerable to over-fitting. This paper presents a Bayesian robust streaming tensor factorization model to identify sparse outliers, automatically determine the underlying tensor rank and accurately fit low-rank structure. We implement our model in Matlab and compare it with existing algorithms on tensor datasets generated from dynamic MRI and Internet traffic.