End-to-End Variational Bayesian Training of Tensorized Neural Networks with Automatic Rank Determination
Paper and Code
Oct 17, 2020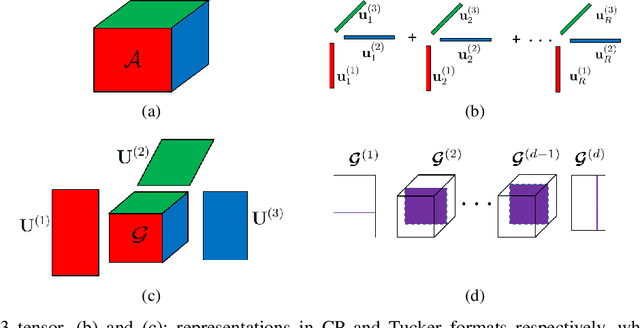
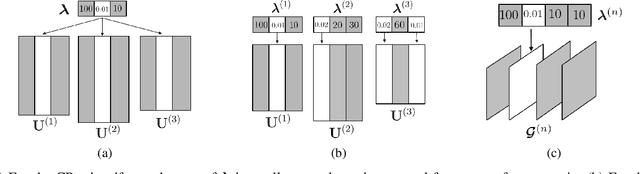
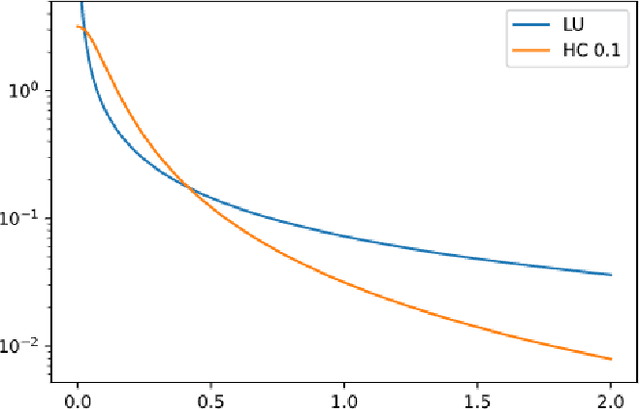
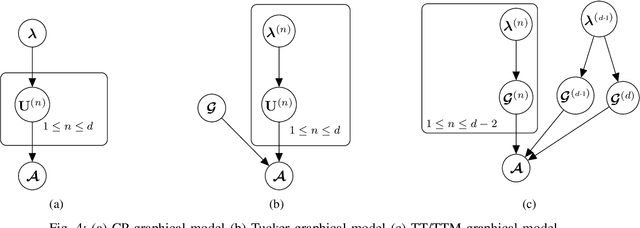
Low-rank tensor decomposition is one of the most effective approaches to reduce the memory and computing requirements of large-size neural networks, enabling their efficient deployment on various hardware platforms. While post-training tensor compression can greatly reduce the cost of inference, uncompressed training still consumes excessive hardware resources, run-time and energy. It is highly desirable to directly train a compact low-rank tensorized model from scratch with a low memory and computational cost. However, this is a very challenging task because it is hard to determine a proper tensor rank a priori, which controls the model complexity and compression ratio in the training process. This paper presents a novel end-to-end framework for low-rank tensorized training of neural networks. We first develop a flexible Bayesian model that can handle various low-rank tensor formats (e.g., CP, Tucker, tensor train and tensor-train matrix) that compress neural network parameters in training. This model can automatically determine the tensor ranks inside a nonlinear forward model, which is beyond the capability of existing Bayesian tensor methods. We further develop a scalable stochastic variational inference solver to estimate the posterior density of large-scale problems in training. Our work provides the first general-purpose rank-adaptive framework for end-to-end tensorized training. Our numerical results on various neural network architectures show orders-of-magnitude parameter reduction and little accuracy loss (or even better accuracy) in the training process.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge