MSV-Mamba: A Multiscale Vision Mamba Network for Echocardiography Segmentation

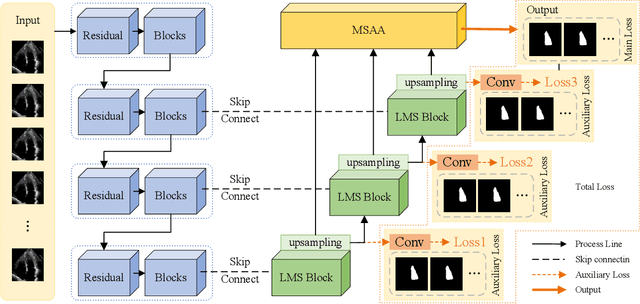
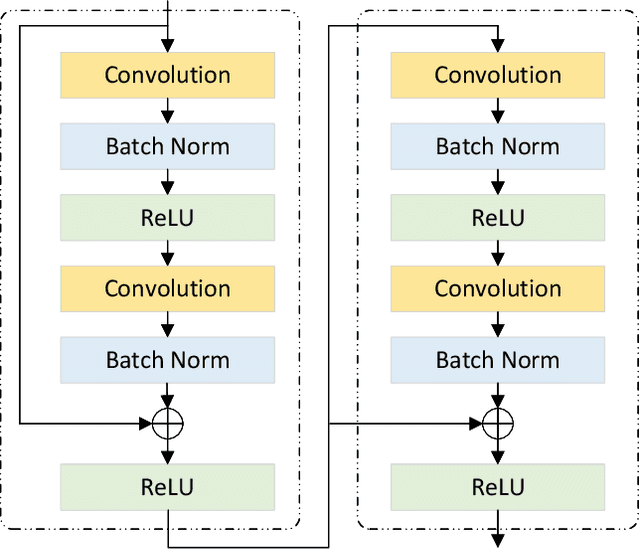
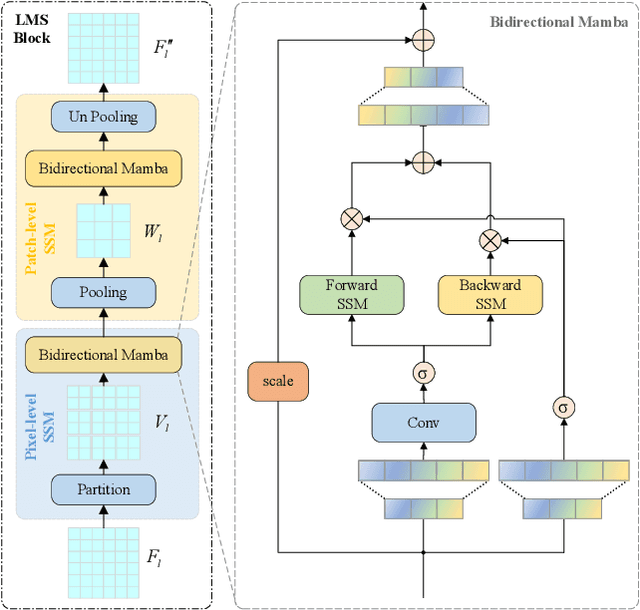
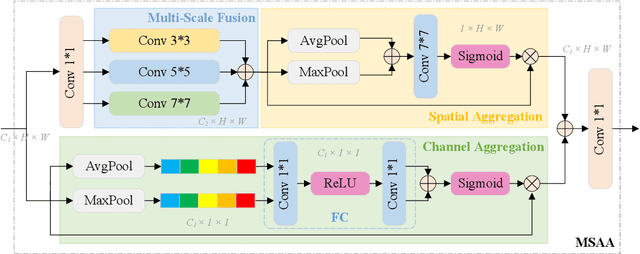
Ultrasound imaging frequently encounters challenges, such as those related to elevated noise levels, diminished spatiotemporal resolution, and the complexity of anatomical structures. These factors significantly hinder the model's ability to accurately capture and analyze structural relationships and dynamic patterns across various regions of the heart. Mamba, an emerging model, is one of the most cutting-edge approaches that is widely applied to diverse vision and language tasks. To this end, this paper introduces a U-shaped deep learning model incorporating a large-window Mamba scale (LMS) module and a hierarchical feature fusion approach for echocardiographic segmentation. First, a cascaded residual block serves as an encoder and is employed to incrementally extract multiscale detailed features. Second, a large-window multiscale mamba module is integrated into the decoder to capture global dependencies across regions and enhance the segmentation capability for complex anatomical structures. Furthermore, our model introduces auxiliary losses at each decoder layer and employs a dual attention mechanism to fuse multilayer features both spatially and across channels. This approach enhances segmentation performance and accuracy in delineating complex anatomical structures. Finally, the experimental results using the EchoNet-Dynamic and CAMUS datasets demonstrate that the model outperforms other methods in terms of both accuracy and robustness. For the segmentation of the left ventricular endocardium (${LV}_{endo}$), the model achieved optimal values of 95.01 and 93.36, respectively, while for the left ventricular epicardium (${LV}_{epi}$), values of 87.35 and 87.80, respectively, were achieved. This represents an improvement ranging between 0.54 and 1.11 compared with the best-performing model.

Leave-One-Out Analysis for Nonconvex Robust Matrix Completion with General Thresholding Functions

We study the problem of robust matrix completion (RMC), where the partially observed entries of an underlying low-rank matrix is corrupted by sparse noise. Existing analysis of the non-convex methods for this problem either requires the explicit but empirically redundant regularization in the algorithm or requires sample splitting in the analysis. In this paper, we consider a simple yet efficient nonconvex method which alternates between a projected gradient step for the low-rank part and a thresholding step for the sparse noise part. Inspired by leave-one out analysis for low rank matrix completion, it is established that the method can achieve linear convergence for a general class of thresholding functions, including for example soft-thresholding and SCAD. To the best of our knowledge, this is the first leave-one-out analysis on a nonconvex method for RMC. Additionally, when applying our result to low rank matrix completion, it improves the sampling complexity of existing result for the singular value projection method.

Elementary Analysis of Policy Gradient Methods

Projected policy gradient under the simplex parameterization, policy gradient and natural policy gradient under the softmax parameterization, are fundamental algorithms in reinforcement learning. There have been a flurry of recent activities in studying these algorithms from the theoretical aspect. Despite this, their convergence behavior is still not fully understood, even given the access to exact policy evaluations. In this paper, we focus on the discounted MDP setting and conduct a systematic study of the aforementioned policy optimization methods. Several novel results are presented, including 1) global linear convergence of projected policy gradient for any constant step size, 2) sublinear convergence of softmax policy gradient for any constant step size, 3) global linear convergence of softmax natural policy gradient for any constant step size, 4) global linear convergence of entropy regularized softmax policy gradient for a wider range of constant step sizes than existing result, 5) tight local linear convergence rate of entropy regularized natural policy gradient, and 6) a new and concise local quadratic convergence rate of soft policy iteration without the assumption on the stationary distribution under the optimal policy. New and elementary analysis techniques have been developed to establish these results.

AutoSAT: Automatically Optimize SAT Solvers via Large Language Models

Heuristics are crucial in SAT solvers, while no heuristic rules are suitable for all problem instances. Therefore, it typically requires to refine specific solvers for specific problem instances. In this context, we present AutoSAT, a novel framework for automatically optimizing heuristics in SAT solvers. AutoSAT is based on Large Large Models (LLMs) which is able to autonomously generate code, conduct evaluation, then utilize the feedback to further optimize heuristics, thereby reducing human intervention and enhancing solver capabilities. AutoSAT operates on a plug-and-play basis, eliminating the need for extensive preliminary setup and model training, and fosters a Chain of Thought collaborative process with fault-tolerance, ensuring robust heuristic optimization. Extensive experiments on a Conflict-Driven Clause Learning (CDCL) solver demonstrates the overall superior performance of AutoSAT, especially in solving some specific SAT problem instances.

Global Convergence of Natural Policy Gradient with Hessian-aided Momentum Variance Reduction

Natural policy gradient (NPG) and its variants are widely-used policy search methods in reinforcement learning. Inspired by prior work, a new NPG variant coined NPG-HM is developed in this paper, which utilizes the Hessian-aided momentum technique for variance reduction, while the sub-problem is solved via the stochastic gradient descent method. It is shown that NPG-HM can achieve the global last iterate $\epsilon$-optimality with a sample complexity of $\mathcal{O}(\epsilon^{-2})$, which is the best known result for natural policy gradient type methods under the generic Fisher non-degenerate policy parameterizations. The convergence analysis is built upon a relaxed weak gradient dominance property tailored for NPG under the compatible function approximation framework, as well as a neat way to decompose the error when handling the sub-problem. Moreover, numerical experiments on Mujoco-based environments demonstrate the superior performance of NPG-HM over other state-of-the-art policy gradient methods.

On the Linear Convergence of Policy Gradient under Hadamard Parameterization

The convergence of deterministic policy gradient under the Hadamard parametrization is studied in the tabular setting and the global linear convergence of the algorithm is established. To this end, we first show that the error decreases at an $O(\frac{1}{k})$ rate for all the iterations. Based on this result, we further show that the algorithm has a faster local linear convergence rate after $k_0$ iterations, where $k_0$ is a constant that only depends on the MDP problem and the step size. Overall, the algorithm displays a linear convergence rate for all the iterations with a loose constant than that for the local linear convergence rate.

Is Attention Better Than Matrix Decomposition?

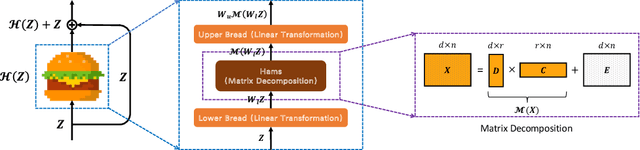
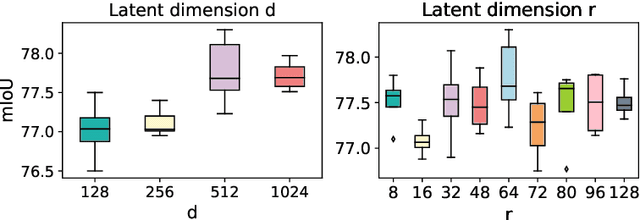
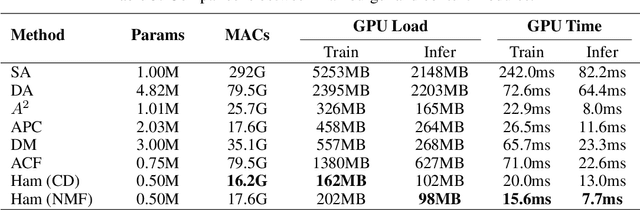
As an essential ingredient of modern deep learning, attention mechanism, especially self-attention, plays a vital role in the global correlation discovery. However, is hand-crafted attention irreplaceable when modeling the global context? Our intriguing finding is that self-attention is not better than the matrix decomposition (MD) model developed 20 years ago regarding the performance and computational cost for encoding the long-distance dependencies. We model the global context issue as a low-rank recovery problem and show that its optimization algorithms can help design global information blocks. This paper then proposes a series of Hamburgers, in which we employ the optimization algorithms for solving MDs to factorize the input representations into sub-matrices and reconstruct a low-rank embedding. Hamburgers with different MDs can perform favorably against the popular global context module self-attention when carefully coping with gradients back-propagated through MDs. Comprehensive experiments are conducted in the vision tasks where it is crucial to learn the global context, including semantic segmentation and image generation, demonstrating significant improvements over self-attention and its variants.

Accelerated Alternating Projections for Robust Principal Component Analysis

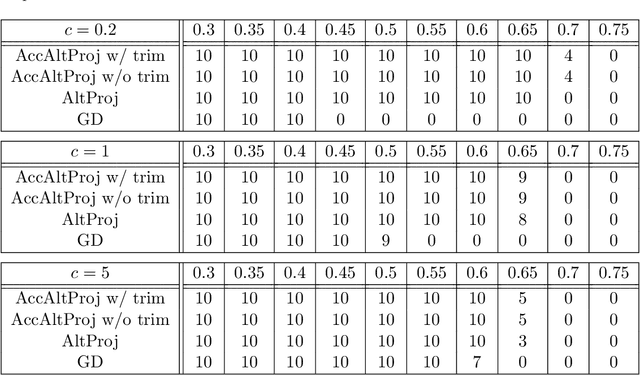
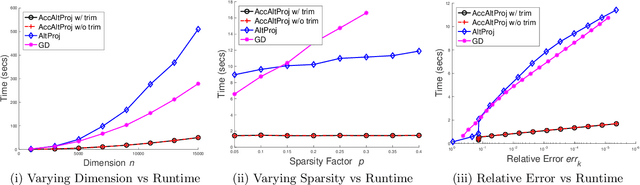
We study robust PCA for the fully observed setting, which is about separating a low rank matrix $\boldsymbol{L}$ and a sparse matrix $\boldsymbol{S}$ from their sum $\boldsymbol{D}=\boldsymbol{L}+\boldsymbol{S}$. In this paper, a new algorithm, dubbed accelerated alternating projections, is introduced for robust PCA which significantly improves the computational efficiency of the existing alternating projections proposed in [Netrapalli, Praneeth, et al., 2014] when updating the low rank factor. The acceleration is achieved by first projecting a matrix onto some low dimensional subspace before obtaining a new estimate of the low rank matrix via truncated SVD. Exact recovery guarantee has been established which shows linear convergence of the proposed algorithm. Empirical performance evaluations establish the advantage of our algorithm over other state-of-the-art algorithms for robust PCA.

New region force for variational models in image segmentation and high dimensional data clustering

We propose an effective framework for multi-phase image segmentation and semi-supervised data clustering by introducing a novel region force term into the Potts model. Assume the probability that a pixel or a data point belongs to each class is known a priori. We show that the corresponding indicator function obeys the Bernoulli distribution and the new region force function can be computed as the negative log-likelihood function under the Bernoulli distribution. We solve the Potts model by the primal-dual hybrid gradient method and the augmented Lagrangian method, which are based on two different dual problems of the same primal problem. Empirical evaluations of the Potts model with the new region force function on benchmark problems show that it is competitive with existing variational methods in both image segmentation and semi-supervised data clustering.