Local Search for Integer Quadratic Programming

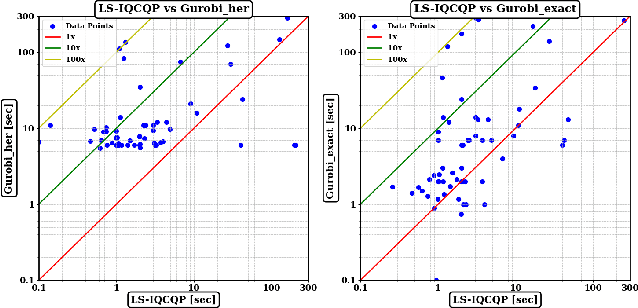
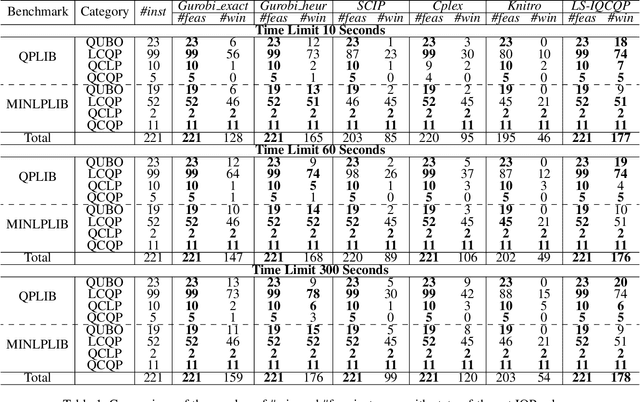
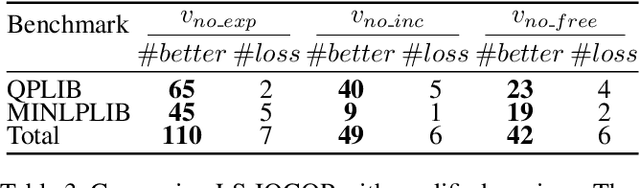
Integer Quadratic Programming (IQP) is an important problem in operations research. Local search is a powerful method for solving hard problems, but the research on local search algorithms for IQP solving is still on its early stage. This paper develops an efficient local search solver for solving general IQP, called LS-IQCQP. We propose four new local search operators for IQP that can handle quadratic terms in the objective function, constraints or both. Furthermore, a two-mode local search algorithm is introduced, utilizing newly designed scoring functions to enhance the search process. Experiments are conducted on standard IQP benchmarks QPLIB and MINLPLIB, comparing LS-IQCQP with several state-of-the-art IQP solvers. Experimental results demonstrate that LS-IQCQP is competitive with the most powerful commercial solver Gurobi and outperforms other state-of-the-art solvers. Moreover, LS-IQCQP has established 6 new records for QPLIB and MINLPLIB open instances.

OPTDTALS: Approximate Logic Synthesis via Optimal Decision Trees Approach

The growing interest in Explainable Artificial Intelligence (XAI) motivates promising studies of computing optimal Interpretable Machine Learning models, especially decision trees. Such models generally provide optimality in compact size or empirical accuracy. Recent works focus on improving efficiency due to the natural scalability issue. The application of such models to practical problems is quite limited. As an emerging problem in circuit design, Approximate Logic Synthesis (ALS) aims to reduce circuit complexity by sacrificing correctness. Recently, multiple heuristic machine learning methods have been applied in ALS, which learns approximated circuits from samples of input-output pairs. In this paper, we propose a new ALS methodology realizing the approximation via learning optimal decision trees in empirical accuracy. Compared to previous heuristic ALS methods, the guarantee of optimality achieves a more controllable trade-off between circuit complexity and accuracy. Experimental results show clear improvements in our methodology in the quality of approximated designs (circuit complexity and accuracy) compared to the state-of-the-art approaches.

ParLS-PBO: A Parallel Local Search Solver for Pseudo Boolean Optimization

As a broadly applied technique in numerous optimization problems, recently, local search has been employed to solve Pseudo-Boolean Optimization (PBO) problem. A representative local search solver for PBO is LSPBO. In this paper, firstly, we improve LSPBO by a dynamic scoring mechanism, which dynamically strikes a balance between score on hard constraints and score on the objective function. Moreover, on top of this improved LSPBO , we develop the first parallel local search PBO solver. The main idea is to share good solutions among different threads to guide the search, by maintaining a pool of feasible solutions. For evaluating solutions when updating the pool, we propose a function that considers both the solution quality and the diversity of the pool. Furthermore, we calculate the polarity density in the pool to enhance the scoring function of local search. Our empirical experiments show clear benefits of the proposed parallel approach, making it competitive with the parallel version of the famous commercial solver Gurobi.

Better Understandings and Configurations in MaxSAT Local Search Solvers via Anytime Performance Analysis

Though numerous solvers have been proposed for the MaxSAT problem, and the benchmark environment such as MaxSAT Evaluations provides a platform for the comparison of the state-of-the-art solvers, existing assessments were usually evaluated based on the quality, e.g., fitness, of the best-found solutions obtained within a given running time budget. However, concerning solely the final obtained solutions regarding specific time budgets may restrict us from comprehending the behavior of the solvers along the convergence process. This paper demonstrates that Empirical Cumulative Distribution Functions can be used to compare MaxSAT local search solvers' anytime performance across multiple problem instances and various time budgets. The assessment reveals distinctions in solvers' performance and displays that the (dis)advantages of solvers adjust along different running times. This work also exhibits that the quantitative and high variance assessment of anytime performance can guide machines, i.e., automatic configurators, to search for better parameter settings. Our experimental results show that the hyperparameter optimization tool, i.e., SMAC, generally achieves better parameter settings of local search when using the anytime performance as the cost function, compared to using the fitness of the best-found solutions.

AutoSAT: Automatically Optimize SAT Solvers via Large Language Models

Heuristics are crucial in SAT solvers, while no heuristic rules are suitable for all problem instances. Therefore, it typically requires to refine specific solvers for specific problem instances. In this context, we present AutoSAT, a novel framework for automatically optimizing heuristics in SAT solvers. AutoSAT is based on Large Large Models (LLMs) which is able to autonomously generate code, conduct evaluation, then utilize the feedback to further optimize heuristics, thereby reducing human intervention and enhancing solver capabilities. AutoSAT operates on a plug-and-play basis, eliminating the need for extensive preliminary setup and model training, and fosters a Chain of Thought collaborative process with fault-tolerance, ensuring robust heuristic optimization. Extensive experiments on a Conflict-Driven Clause Learning (CDCL) solver demonstrates the overall superior performance of AutoSAT, especially in solving some specific SAT problem instances.

Local Search for Integer Linear Programming

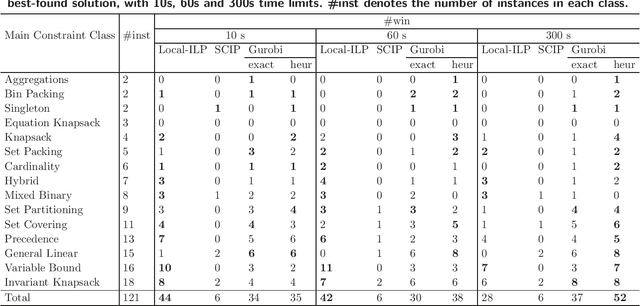
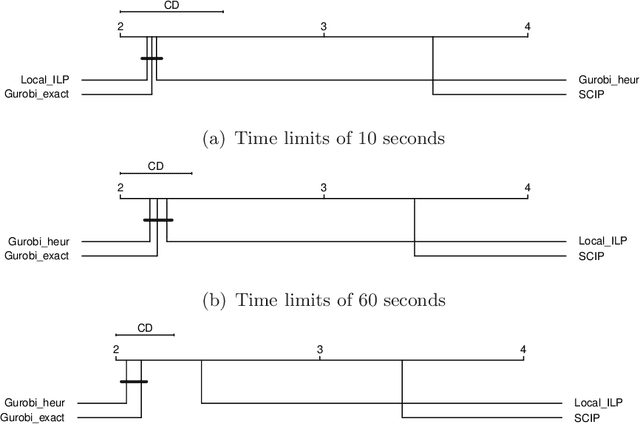
Integer linear programming models a wide range of practical combinatorial optimization problems and has significant impacts in industry and management sectors. This work develops the first standalone local search solver for general integer linear programming validated on a large heterogeneous problem dataset. We propose a local search framework that switches in three modes, namely Search, Improve, and Restore modes, and design tailored operators adapted to different modes, thus improve the quality of the current solution according to different situations. For the Search and Restore modes, we propose an operator named tight move, which adaptively modifies variables' values trying to make some constraint tight. For the Improve mode, an efficient operator lift move is proposed to improve the quality of the objective function while maintaining feasibility. Putting these together, we develop a local search solver for integer linear programming called Local-ILP. Experiments conducted on the MIPLIB dataset show the effectiveness of our solver in solving large-scale hard integer linear programming problems within a reasonably short time. Local-ILP is competitive and complementary to the state-of-the-art commercial solver Gurobi and significantly outperforms the state-of-the-art non-commercial solver SCIP. Moreover, our solver establishes new records for 6 MIPLIB open instances.

LANDMARK: Language-guided Representation Enhancement Framework for Scene Graph Generation

Scene graph generation (SGG) is a sophisticated task that suffers from both complex visual features and dataset long-tail problem. Recently, various unbiased strategies have been proposed by designing novel loss functions and data balancing strategies. Unfortunately, these unbiased methods fail to emphasize language priors in feature refinement perspective. Inspired by the fact that predicates are highly correlated with semantics hidden in subject-object pair and global context, we propose LANDMARK (LANguage-guiDed representationenhanceMent frAmewoRK) that learns predicate-relevant representations from language-vision interactive patterns, global language context and pair-predicate correlation. Specifically, we first project object labels to three distinctive semantic embeddings for different representation learning. Then, Language Attention Module (LAM) and Experience Estimation Module (EEM) process subject-object word embeddings to attention vector and predicate distribution, respectively. Language Context Module (LCM) encodes global context from each word embed-ding, which avoids isolated learning from local information. Finally, modules outputs are used to update visual representations and SGG model's prediction. All language representations are purely generated from object categories so that no extra knowledge is needed. This framework is model-agnostic and consistently improves performance on existing SGG models. Besides, representation-level unbiased strategies endow LANDMARK the advantage of compatibility with other methods. Code is available at https://github.com/rafa-cxg/PySGG-cxg.

Incremental Satisfiability Modulo Theory for Verification of Deep Neural Networks

Constraint solving is an elementary way for verification of deep neural networks (DNN). In the domain of AI safety, a DNN might be modified in its structure and parameters for its repair or attack. For such situations, we propose the incremental DNN verification problem, which asks whether a safety property still holds after the DNN is modified. To solve the problem, we present an incremental satisfiability modulo theory (SMT) algorithm based on the Reluplex framework. We simulate the most important features of the configurations that infers the verification result of the searching branches in the old solving procedure (with respect to the original network), and heuristically check whether the proofs are still valid for the modified DNN. We implement our algorithm as an incremental solver called DeepInc, and exerimental results show that DeepInc is more efficient in most cases. For the cases that the property holds both before and after modification, the acceleration can be faster by several orders of magnitude, showing that DeepInc is outstanding in incrementally searching for counterexamples. Moreover, based on the framework, we propose the multi-objective DNN repair problem and give an algorithm based on our incremental SMT solving algorithm. Our repair method preserves more potential safety properties on the repaired DNNs compared with state-of-the-art.

Can Graph Neural Networks Learn to Solve MaxSAT Problem?

With the rapid development of deep learning techniques, various recent work has tried to apply graph neural networks (GNNs) to solve NP-hard problems such as Boolean Satisfiability (SAT), which shows the potential in bridging the gap between machine learning and symbolic reasoning. However, the quality of solutions predicted by GNNs has not been well investigated in the literature. In this paper, we study the capability of GNNs in learning to solve Maximum Satisfiability (MaxSAT) problem, both from theoretical and practical perspectives. We build two kinds of GNN models to learn the solution of MaxSAT instances from benchmarks, and show that GNNs have attractive potential to solve MaxSAT problem through experimental evaluation. We also present a theoretical explanation of the effect that GNNs can learn to solve MaxSAT problem to some extent for the first time, based on the algorithmic alignment theory.

NLocalSAT: Boosting Local Search with Solution Prediction

The boolean satisfiability problem is a famous NP-complete problem in computer science. An effective way for this problem is the stochastic local search (SLS). However, in this method, the initialization is assigned in a random manner, which impacts the effectiveness of SLS solvers. To address this problem, we propose NLocalSAT. NLocalSAT combines SLS with a solution prediction model, which boosts SLS by changing initialization assignments with a neural network. We evaluated NLocalSAT on five SLS solvers (CCAnr, Sparrow, CPSparrow, YalSAT, and probSAT) with problems in the random track of SAT Competition 2018. The experimental results show that solvers with NLocalSAT achieve 27%~62% improvement over the original SLS solvers.