Can Graph Neural Networks Learn to Solve MaxSAT Problem?

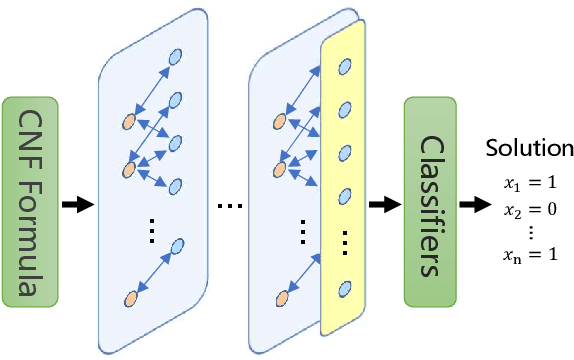
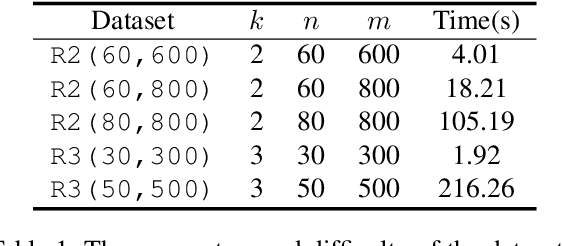
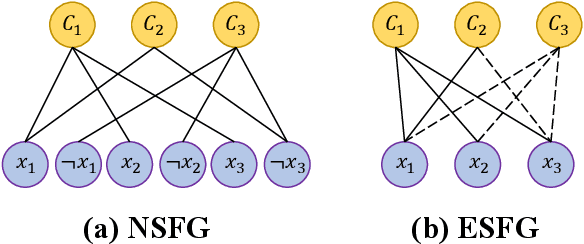
With the rapid development of deep learning techniques, various recent work has tried to apply graph neural networks (GNNs) to solve NP-hard problems such as Boolean Satisfiability (SAT), which shows the potential in bridging the gap between machine learning and symbolic reasoning. However, the quality of solutions predicted by GNNs has not been well investigated in the literature. In this paper, we study the capability of GNNs in learning to solve Maximum Satisfiability (MaxSAT) problem, both from theoretical and practical perspectives. We build two kinds of GNN models to learn the solution of MaxSAT instances from benchmarks, and show that GNNs have attractive potential to solve MaxSAT problem through experimental evaluation. We also present a theoretical explanation of the effect that GNNs can learn to solve MaxSAT problem to some extent for the first time, based on the algorithmic alignment theory.

ε-weakened Robustness of Deep Neural Networks

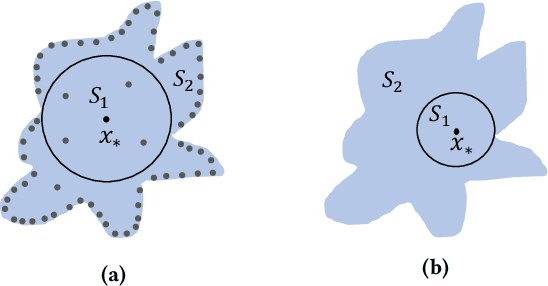
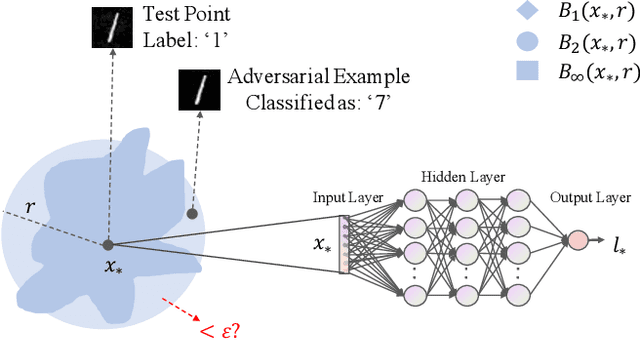
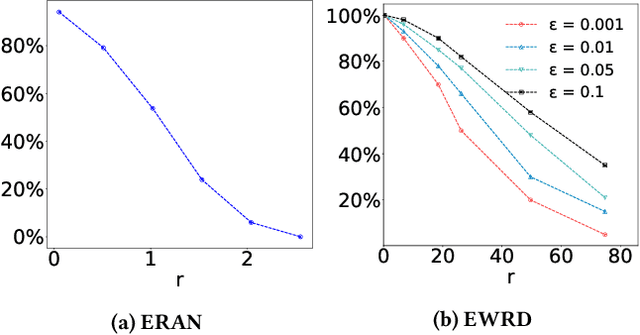
This paper introduces a notation of $\varepsilon$-weakened robustness for analyzing the reliability and stability of deep neural networks (DNNs). Unlike the conventional robustness, which focuses on the "perfect" safe region in the absence of adversarial examples, $\varepsilon$-weakened robustness focuses on the region where the proportion of adversarial examples is bounded by user-specified $\varepsilon$. Smaller $\varepsilon$ means a smaller chance of failure. Under such robustness definition, we can give conclusive results for the regions where conventional robustness ignores. We prove that the $\varepsilon$-weakened robustness decision problem is PP-complete and give a statistical decision algorithm with user-controllable error bound. Furthermore, we derive an algorithm to find the maximum $\varepsilon$-weakened robustness radius. The time complexity of our algorithms is polynomial in the dimension and size of the network. So, they are scalable to large real-world networks. Besides, We also show its potential application in analyzing quality issues.