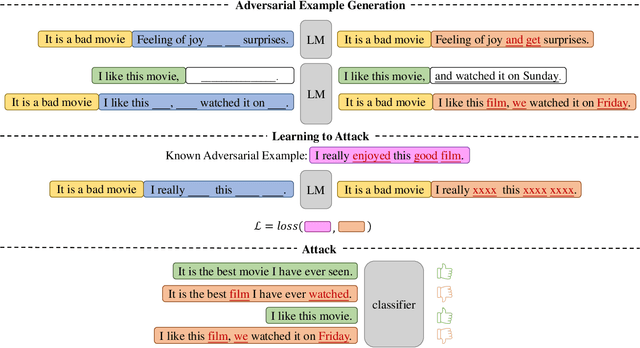
A Prompting-based Approach for Adversarial Example Generation and Robustness Enhancement

Recent years have seen the wide application of NLP models in crucial areas such as finance, medical treatment, and news media, raising concerns of the model robustness and vulnerabilities. In this paper, we propose a novel prompt-based adversarial attack to compromise NLP models and robustness enhancement technique. We first construct malicious prompts for each instance and generate adversarial examples via mask-and-filling under the effect of a malicious purpose. Our attack technique targets the inherent vulnerabilities of NLP models, allowing us to generate samples even without interacting with the victim NLP model, as long as it is based on pre-trained language models (PLMs). Furthermore, we design a prompt-based adversarial training method to improve the robustness of PLMs. As our training method does not actually generate adversarial samples, it can be applied to large-scale training sets efficiently. The experimental results show that our attack method can achieve a high attack success rate with more diverse, fluent and natural adversarial examples. In addition, our robustness enhancement method can significantly improve the robustness of models to resist adversarial attacks. Our work indicates that prompting paradigm has great potential in probing some fundamental flaws of PLMs and fine-tuning them for downstream tasks.

Can Graph Neural Networks Learn to Solve MaxSAT Problem?

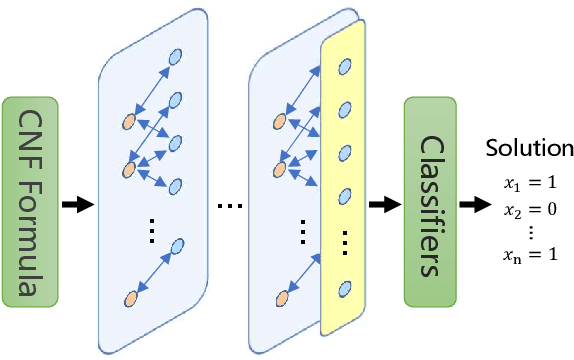
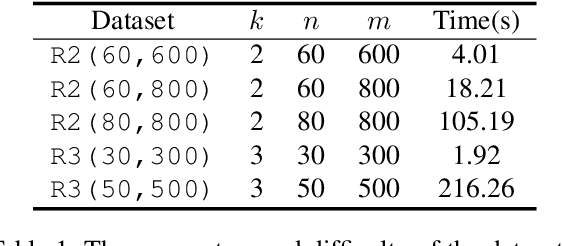
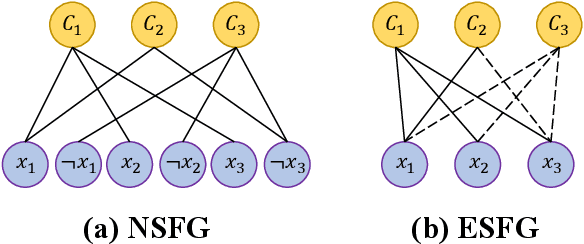
With the rapid development of deep learning techniques, various recent work has tried to apply graph neural networks (GNNs) to solve NP-hard problems such as Boolean Satisfiability (SAT), which shows the potential in bridging the gap between machine learning and symbolic reasoning. However, the quality of solutions predicted by GNNs has not been well investigated in the literature. In this paper, we study the capability of GNNs in learning to solve Maximum Satisfiability (MaxSAT) problem, both from theoretical and practical perspectives. We build two kinds of GNN models to learn the solution of MaxSAT instances from benchmarks, and show that GNNs have attractive potential to solve MaxSAT problem through experimental evaluation. We also present a theoretical explanation of the effect that GNNs can learn to solve MaxSAT problem to some extent for the first time, based on the algorithmic alignment theory.

ε-weakened Robustness of Deep Neural Networks

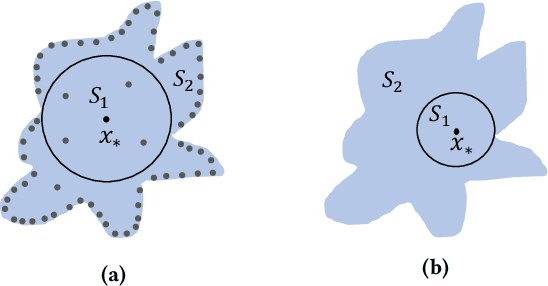
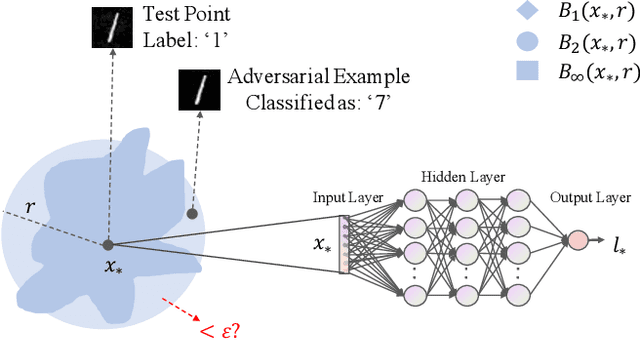
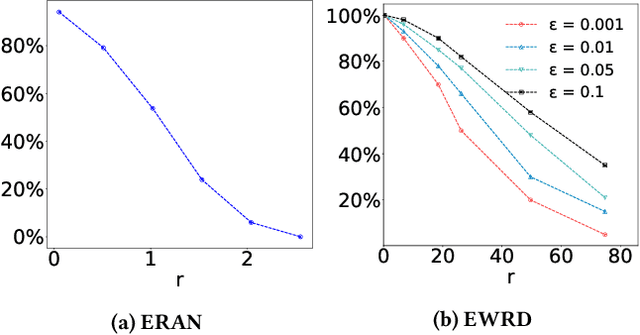
This paper introduces a notation of $\varepsilon$-weakened robustness for analyzing the reliability and stability of deep neural networks (DNNs). Unlike the conventional robustness, which focuses on the "perfect" safe region in the absence of adversarial examples, $\varepsilon$-weakened robustness focuses on the region where the proportion of adversarial examples is bounded by user-specified $\varepsilon$. Smaller $\varepsilon$ means a smaller chance of failure. Under such robustness definition, we can give conclusive results for the regions where conventional robustness ignores. We prove that the $\varepsilon$-weakened robustness decision problem is PP-complete and give a statistical decision algorithm with user-controllable error bound. Furthermore, we derive an algorithm to find the maximum $\varepsilon$-weakened robustness radius. The time complexity of our algorithms is polynomial in the dimension and size of the network. So, they are scalable to large real-world networks. Besides, We also show its potential application in analyzing quality issues.

Counting the Number of Solutions to Constraints

Compared with constraint satisfaction problems, counting problems have received less attention. In this paper, we survey research works on the problems of counting the number of solutions to constraints. The constraints may take various forms, including, formulas in the propositional logic, linear inequalities over the reals or integers, Boolean combination of linear constraints. We describe some techniques and tools for solving the counting problems, as well as some applications (e.g., applications to automated reasoning, program analysis, formal verification and information security).

ACFNet: Attentional Class Feature Network for Semantic Segmentation

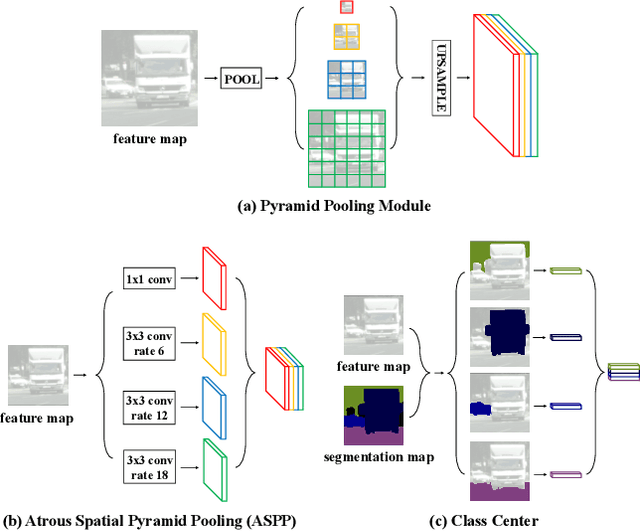
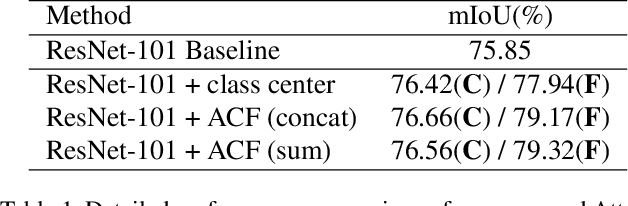
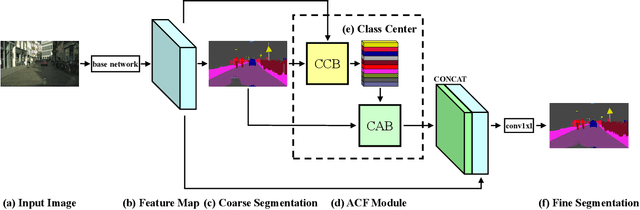
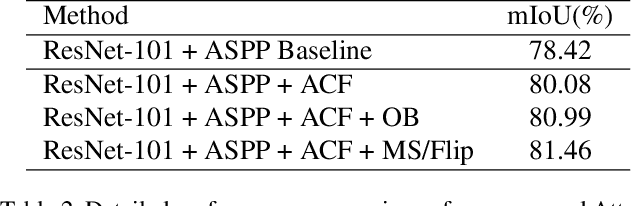
Recent works have made great progress in semantic segmentation by exploiting richer context, most of which are designed from a spatial perspective. In contrast to previous works, we present the concept of class center which extracts the global context from a categorical perspective. This class-level context describes the overall representation of each class in an image. We further propose a novel module, named Attentional Class Feature (ACF) module, to calculate and adaptively combine different class centers according to each pixel. Based on the ACF module, we introduce a coarse-to-fine segmentation network, called Attentional Class Feature Network (ACFNet), which can be composed of an ACF module and any off-the-shell segmentation network (base network). In this paper, we use two types of base networks to evaluate the effectiveness of ACFNet. We achieve new state-of-the-art performance of 81.85% mIoU on Cityscapes dataset with only finely annotated data used for training.

A New Probabilistic Algorithm for Approximate Model Counting

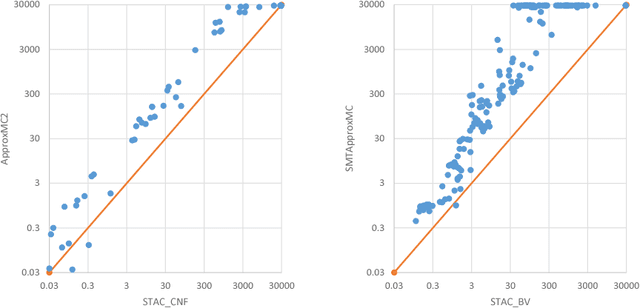
Constrained counting is important in domains ranging from artificial intelligence to software analysis. There are already a few approaches for counting models over various types of constraints. Recently, hashing-based approaches achieve both theoretical guarantees and scalability, but still rely on solution enumeration. In this paper, a new probabilistic polynomial time approximate model counter is proposed, which is also a hashing-based universal framework, but with only satisfiability queries. A variant with a dynamic stopping criterion is also presented. Empirical evaluation over benchmarks on propositional logic formulas and SMT(BV) formulas shows that the approach is promising.

Diversified Top-k Partial MaxSAT Solving

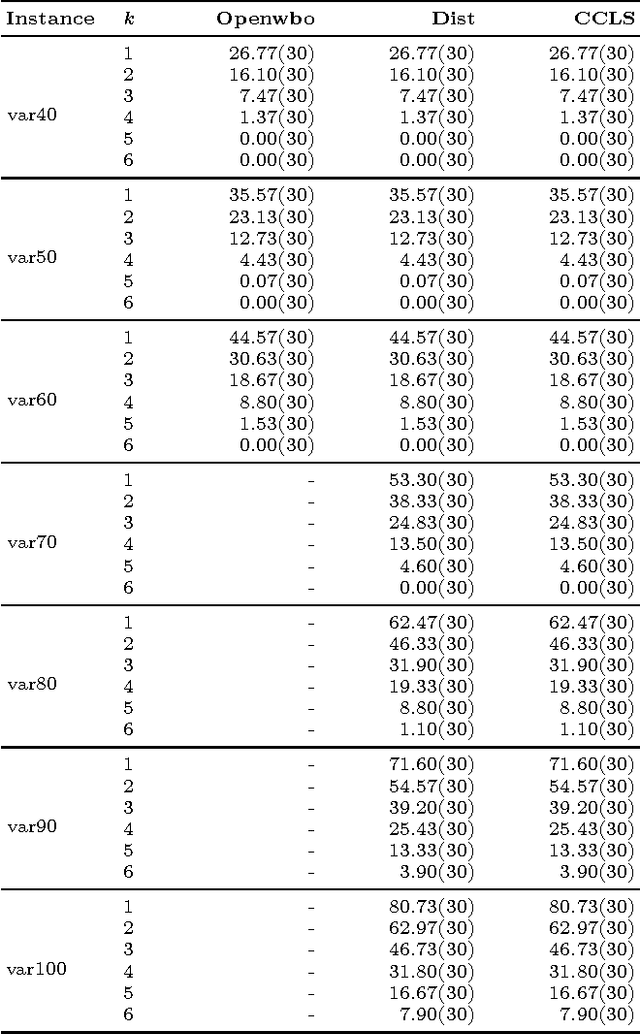
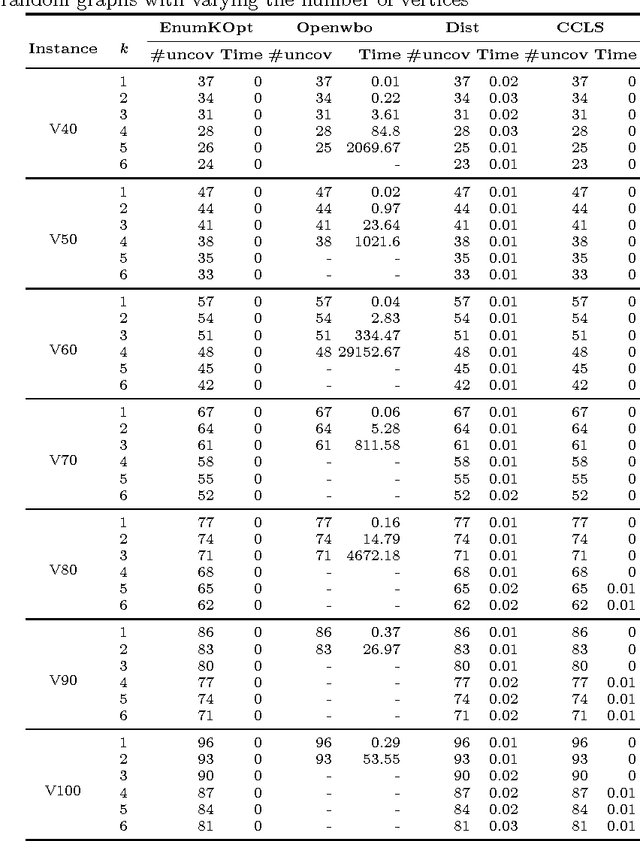
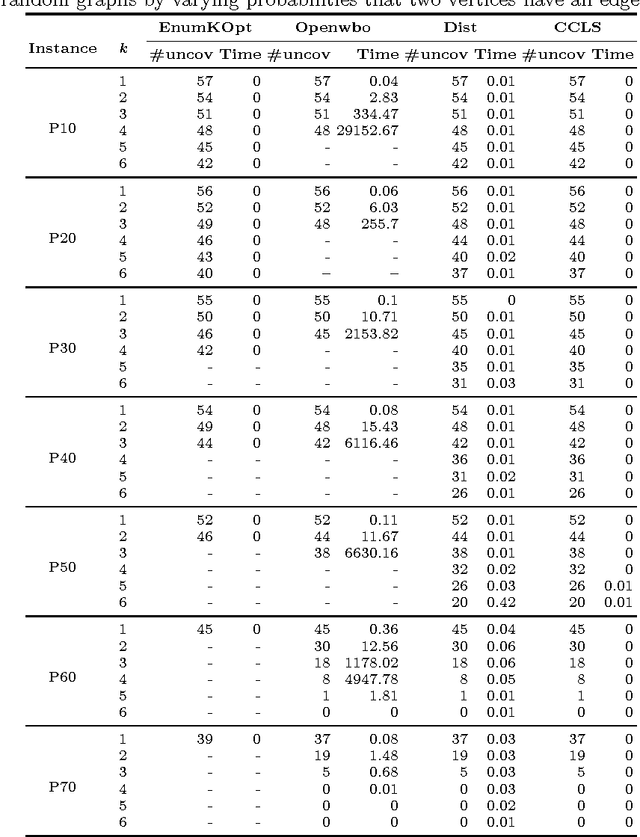
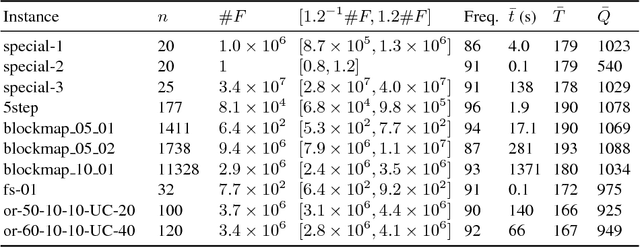
We introduce a diversified top-k partial MaxSAT problem, a combination of partial MaxSAT problem and enumeration problem. Given a partial MaxSAT formula F and a positive integer k, the diversified top-k partial MaxSAT is to find k maximal solutions for F such that the k maximal solutions satisfy the maximum number of soft clauses of F. This problem can be widely used in many applications including community detection, sensor place, motif discovery, and combinatorial testing. We prove the problem is NP-hard and propose an approach for solving the problem. The concrete idea of the approach is to design an encoding EE which reduces diversified top-k partial MaxSAT problem into partial MaxSAT problem, and then solve the resulting problem with state-of-art solvers. In addition, we present an algorithm MEMKC exactly solving the diversified top-k partial MaxSAT. Through several experiments we show that our approach can be successfully applied to the interesting problem.

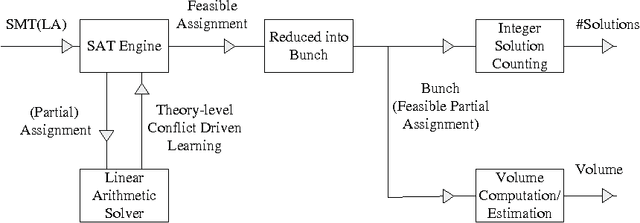
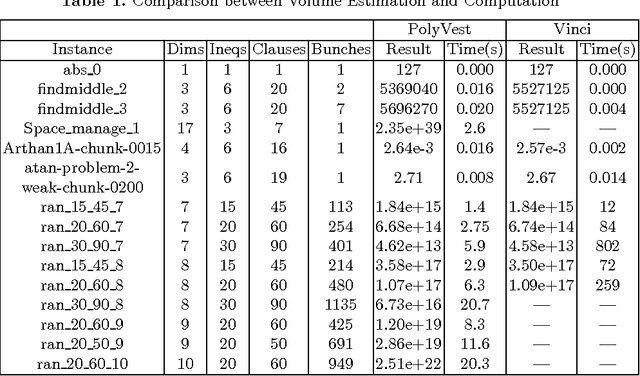
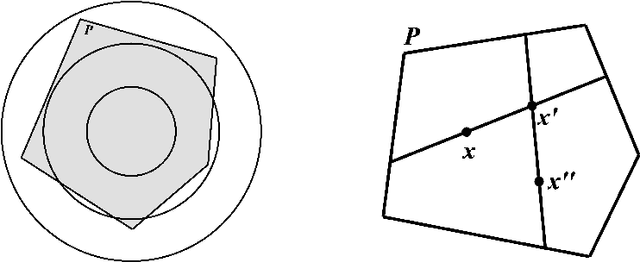
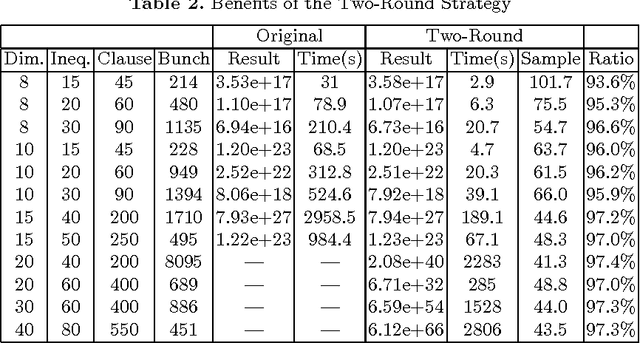
A Tool for Computing and Estimating the Volume of the Solution Space of SMT

There are already quite a few tools for solving the Satisfiability Modulo Theories (SMT) problems. In this paper, we present \texttt{VolCE}, a tool for counting the solutions of SMT constraints, or in other words, for computing the volume of the solution space. Its input is essentially a set of Boolean combinations of linear constraints, where the numeric variables are either all integers or all reals, and each variable is bounded. The tool extends SMT solving with integer solution counting and volume computation/estimation for convex polytopes. Effective heuristics are adopted, which enable the tool to deal with high-dimensional problem instances efficiently and accurately.