Diversified Top-k Partial MaxSAT Solving

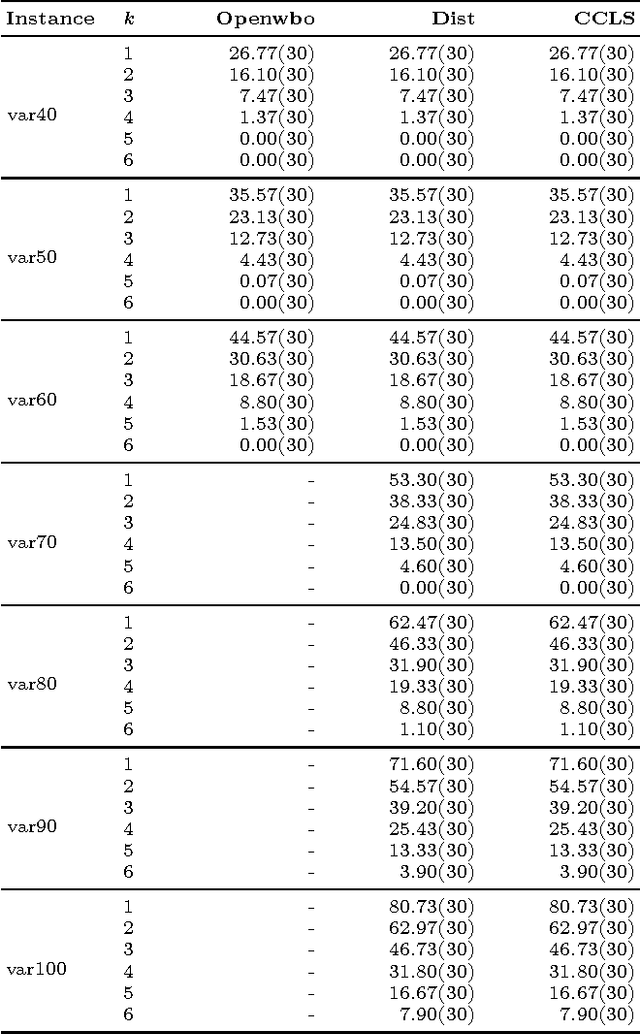
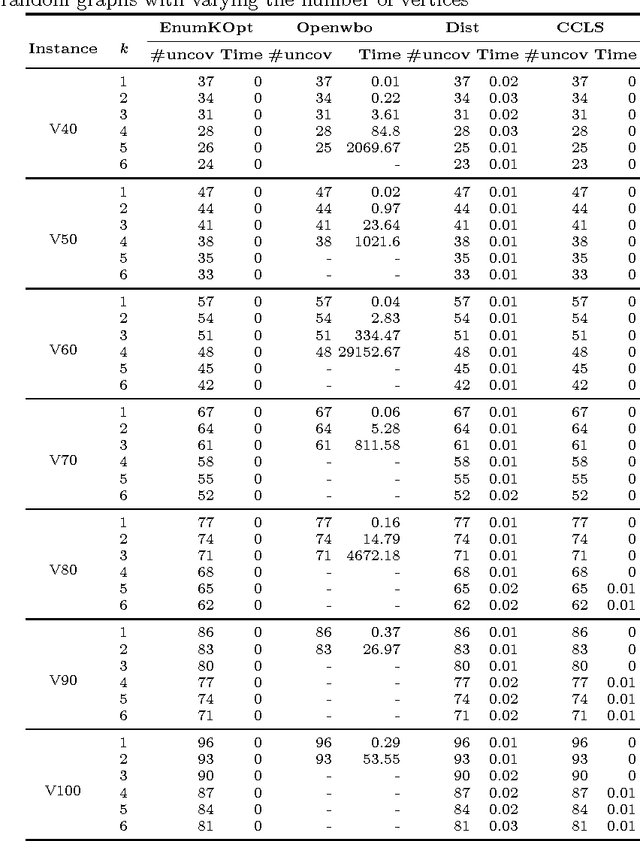
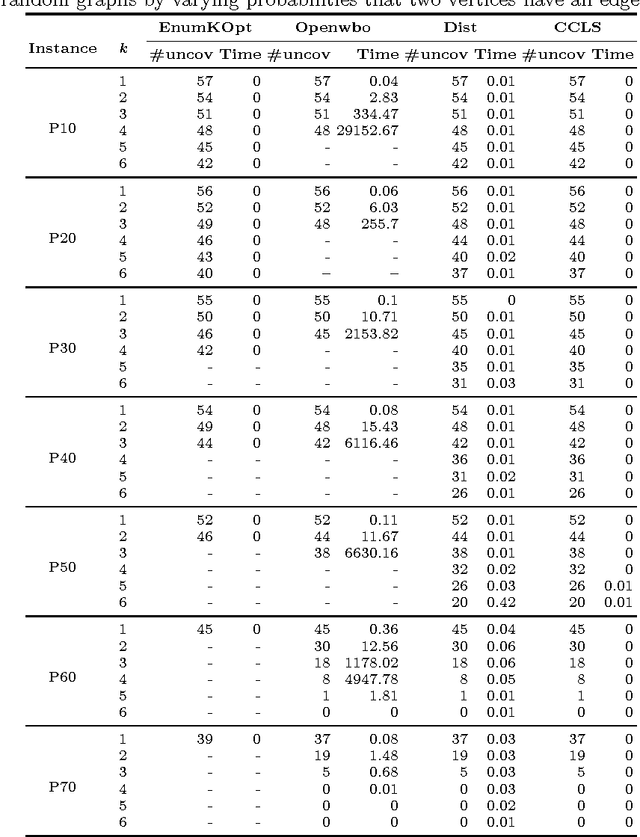
We introduce a diversified top-k partial MaxSAT problem, a combination of partial MaxSAT problem and enumeration problem. Given a partial MaxSAT formula F and a positive integer k, the diversified top-k partial MaxSAT is to find k maximal solutions for F such that the k maximal solutions satisfy the maximum number of soft clauses of F. This problem can be widely used in many applications including community detection, sensor place, motif discovery, and combinatorial testing. We prove the problem is NP-hard and propose an approach for solving the problem. The concrete idea of the approach is to design an encoding EE which reduces diversified top-k partial MaxSAT problem into partial MaxSAT problem, and then solve the resulting problem with state-of-art solvers. In addition, we present an algorithm MEMKC exactly solving the diversified top-k partial MaxSAT. Through several experiments we show that our approach can be successfully applied to the interesting problem.

Approximate Counting CSP Solutions Using Partition Function

We propose a new approximate method for counting the number of the solutions for constraint satisfaction problem (CSP). The method derives from the partition function based on introducing the free energy and capturing the relationship of probabilities of variables and constraints, which requires the marginal probabilities. It firstly obtains the marginal probabilities using the belief propagation, and then computes the number of solutions according to the partition function. This allows us to directly plug the marginal probabilities into the partition function and efficiently count the number of solutions for CSP. The experimental results show that our method can solve both random problems and structural problems efficiently.

Hybrid Tractable Classes of Binary Quantified Constraint Satisfaction Problems

In this paper, we investigate the hybrid tractability of binary Quantified Constraint Satisfaction Problems (QCSPs). First, a basic tractable class of binary QCSPs is identified by using the broken-triangle property. In this class, the variable ordering for the broken-triangle property must be same as that in the prefix of the QCSP. Second, we break this restriction to allow that existentially quantified variables can be shifted within or out of their blocks, and thus identify some novel tractable classes by introducing the broken-angle property. Finally, we identify a more generalized tractable class, i.e., the min-of-max extendable class for QCSPs.

New Worst-Case Upper Bound for X3SAT

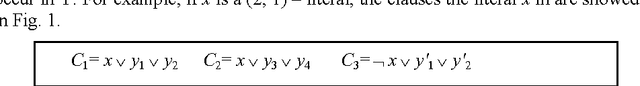
The rigorous theoretical analyses of algorithms for exact 3-satisfiability (X3SAT) have been proposed in the literature. As we know, previous algorithms for solving X3SAT have been analyzed only regarding the number of variables as the parameter. However, the time complexity for solving X3SAT instances depends not only on the number of variables, but also on the number of clauses. Therefore, it is significant to exploit the time complexity from the other point of view, i.e. the number of clauses. In this paper, we present algorithms for solving X3SAT with rigorous complexity analyses using the number of clauses as the parameter. By analyzing the algorithms, we obtain the new worst-case upper bounds O(1.15855m), where m is the number of clauses.

New Worst-Case Upper Bound for #XSAT

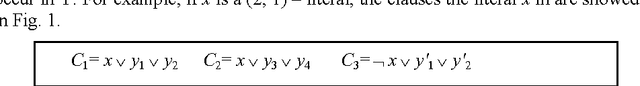
An algorithm running in O(1.1995n) is presented for counting models for exact satisfiability formulae(#XSAT). This is faster than the previously best algorithm which runs in O(1.2190n). In order to improve the efficiency of the algorithm, a new principle, i.e. the common literals principle, is addressed to simplify formulae. This allows us to eliminate more common literals. In addition, we firstly inject the resolution principles into solving #XSAT problem, and therefore this further improves the efficiency of the algorithm.

Phase Transitions of Plan Modification in Conformant Planning

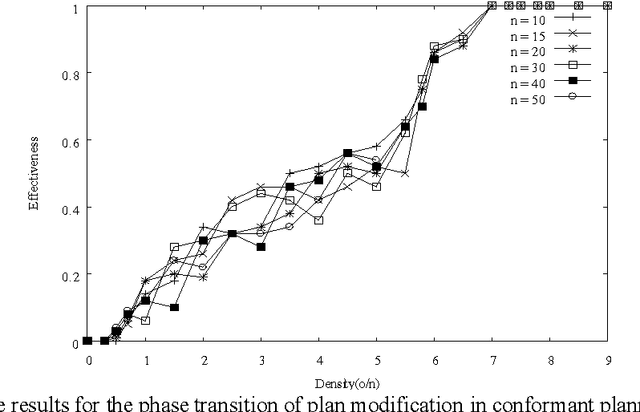
We explore phase transitions of plan modification, which mainly focus on the conformant planning problems. By analyzing features of plan modification in conformant planning problems, quantitative results are obtained. If the number of operators is less than, almost all conformant planning problems can't be solved with plan modification. If the number of operators is more than, almost all conformant planning problems can be solved with plan modification. The results of the experiments also show that there exists an experimental threshold of density (ratio of number of operators to number of propositions), which separates the region where almost all conformant planning problems can't be solved with plan modification from the region where almost all conformant planning problems can be solved with plan modification.

New worst upper bound for #SAT

The rigorous theoretical analyses of algorithms for #SAT have been proposed in the literature. As we know, previous algorithms for solving #SAT have been analyzed only regarding the number of variables as the parameter. However, the time complexity for solving #SAT instances depends not only on the number of variables, but also on the number of clauses. Therefore, it is significant to exploit the time complexity from the other point of view, i.e. the number of clauses. In this paper, we present algorithms for solving #2-SAT and #3-SAT with rigorous complexity analyses using the number of clauses as the parameter. By analyzing the algorithms, we obtain the new worst-case upper bounds O(1.1892m) for #2-SAT and O(1.4142m) for #3-SAT, where m is the number of clauses.