ε-weakened Robustness of Deep Neural Networks
Paper and Code
Oct 29, 2021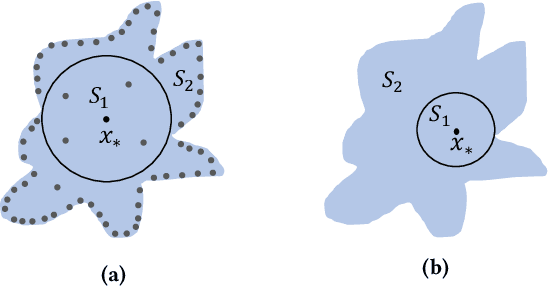

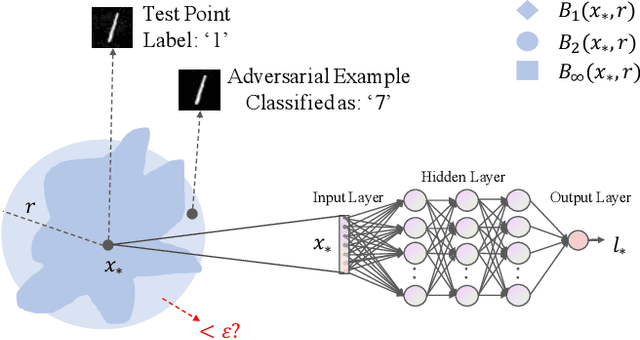
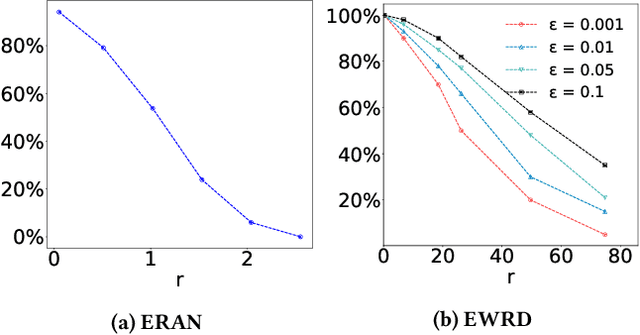
This paper introduces a notation of $\varepsilon$-weakened robustness for analyzing the reliability and stability of deep neural networks (DNNs). Unlike the conventional robustness, which focuses on the "perfect" safe region in the absence of adversarial examples, $\varepsilon$-weakened robustness focuses on the region where the proportion of adversarial examples is bounded by user-specified $\varepsilon$. Smaller $\varepsilon$ means a smaller chance of failure. Under such robustness definition, we can give conclusive results for the regions where conventional robustness ignores. We prove that the $\varepsilon$-weakened robustness decision problem is PP-complete and give a statistical decision algorithm with user-controllable error bound. Furthermore, we derive an algorithm to find the maximum $\varepsilon$-weakened robustness radius. The time complexity of our algorithms is polynomial in the dimension and size of the network. So, they are scalable to large real-world networks. Besides, We also show its potential application in analyzing quality issues.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge