How to Inverting the Leverage Score Distribution?

Leverage score is a fundamental problem in machine learning and theoretical computer science. It has extensive applications in regression analysis, randomized algorithms, and neural network inversion. Despite leverage scores are widely used as a tool, in this paper, we study a novel problem, namely the inverting leverage score problem. We analyze to invert the leverage score distributions back to recover model parameters. Specifically, given a leverage score $\sigma \in \mathbb{R}^n$, the matrix $A \in \mathbb{R}^{n \times d}$, and the vector $b \in \mathbb{R}^n$, we analyze the non-convex optimization problem of finding $x \in \mathbb{R}^d$ to minimize $\| \mathrm{diag}( \sigma ) - I_n \circ (A(x) (A(x)^\top A(x) )^{-1} A(x)^\top ) \|_F$, where $A(x):= S(x)^{-1} A \in \mathbb{R}^{n \times d} $, $S(x) := \mathrm{diag}(s(x)) \in \mathbb{R}^{n \times n}$ and $s(x) : = Ax - b \in \mathbb{R}^n$. Our theoretical studies include computing the gradient and Hessian, demonstrating that the Hessian matrix is positive definite and Lipschitz, and constructing first-order and second-order algorithms to solve this regression problem. Our work combines iterative shrinking and the induction hypothesis to ensure global convergence rates for the Newton method, as well as the properties of Lipschitz and strong convexity to guarantee the performance of gradient descent. This important study on inverting statistical leverage opens up numerous new applications in interpretation, data recovery, and security.

Local Convergence of Approximate Newton Method for Two Layer Nonlinear Regression

There have been significant advancements made by large language models (LLMs) in various aspects of our daily lives. LLMs serve as a transformative force in natural language processing, finding applications in text generation, translation, sentiment analysis, and question-answering. The accomplishments of LLMs have led to a substantial increase in research efforts in this domain. One specific two-layer regression problem has been well-studied in prior works, where the first layer is activated by a ReLU unit, and the second layer is activated by a softmax unit. While previous works provide a solid analysis of building a two-layer regression, there is still a gap in the analysis of constructing regression problems with more than two layers. In this paper, we take a crucial step toward addressing this problem: we provide an analysis of a two-layer regression problem. In contrast to previous works, our first layer is activated by a softmax unit. This sets the stage for future analyses of creating more activation functions based on the softmax function. Rearranging the softmax function leads to significantly different analyses. Our main results involve analyzing the convergence properties of an approximate Newton method used to minimize the regularized training loss. We prove that the loss function for the Hessian matrix is positive definite and Lipschitz continuous under certain assumptions. This enables us to establish local convergence guarantees for the proposed training algorithm. Specifically, with an appropriate initialization and after $O(\log(1/\epsilon))$ iterations, our algorithm can find an $\epsilon$-approximate minimizer of the training loss with high probability. Each iteration requires approximately $O(\mathrm{nnz}(C) + d^\omega)$ time, where $d$ is the model size, $C$ is the input matrix, and $\omega < 2.374$ is the matrix multiplication exponent.

Zero-th Order Algorithm for Softmax Attention Optimization

Large language models (LLMs) have brought about significant transformations in human society. Among the crucial computations in LLMs, the softmax unit holds great importance. Its helps the model generating a probability distribution on potential subsequent words or phrases, considering a series of input words. By utilizing this distribution, the model selects the most probable next word or phrase, based on the assigned probabilities. The softmax unit assumes a vital function in LLM training as it facilitates learning from data through the adjustment of neural network weights and biases. With the development of the size of LLMs, computing the gradient becomes expensive. However, Zero-th Order method can approximately compute the gradient with only forward passes. In this paper, we present a Zero-th Order algorithm specifically tailored for Softmax optimization. We demonstrate the convergence of our algorithm, highlighting its effectiveness in efficiently computing gradients for large-scale LLMs. By leveraging the Zeroth-Order method, our work contributes to the advancement of optimization techniques in the context of complex language models.

Attention Scheme Inspired Softmax Regression

Large language models (LLMs) have made transformed changes for human society. One of the key computation in LLMs is the softmax unit. This operation is important in LLMs because it allows the model to generate a distribution over possible next words or phrases, given a sequence of input words. This distribution is then used to select the most likely next word or phrase, based on the probabilities assigned by the model. The softmax unit plays a crucial role in training LLMs, as it allows the model to learn from the data by adjusting the weights and biases of the neural network. In the area of convex optimization such as using central path method to solve linear programming. The softmax function has been used a crucial tool for controlling the progress and stability of potential function [Cohen, Lee and Song STOC 2019, Brand SODA 2020]. In this work, inspired the softmax unit, we define a softmax regression problem. Formally speaking, given a matrix $A \in \mathbb{R}^{n \times d}$ and a vector $b \in \mathbb{R}^n$, the goal is to use greedy type algorithm to solve \begin{align*} \min_{x} \| \langle \exp(Ax), {\bf 1}_n \rangle^{-1} \exp(Ax) - b \|_2^2. \end{align*} In certain sense, our provable convergence result provides theoretical support for why we can use greedy algorithm to train softmax function in practice.

Solving Regularized Exp, Cosh and Sinh Regression Problems

In modern machine learning, attention computation is a fundamental task for training large language models such as Transformer, GPT-4 and ChatGPT. In this work, we study exponential regression problem which is inspired by the softmax/exp unit in the attention mechanism in large language models. The standard exponential regression is non-convex. We study the regularization version of exponential regression problem which is a convex problem. We use approximate newton method to solve in input sparsity time. Formally, in this problem, one is given matrix $A \in \mathbb{R}^{n \times d}$, $b \in \mathbb{R}^n$, $w \in \mathbb{R}^n$ and any of functions $\exp, \cosh$ and $\sinh$ denoted as $f$. The goal is to find the optimal $x$ that minimize $ 0.5 \| f(Ax) - b \|_2^2 + 0.5 \| \mathrm{diag}(w) A x \|_2^2$. The straightforward method is to use the naive Newton's method. Let $\mathrm{nnz}(A)$ denote the number of non-zeros entries in matrix $A$. Let $\omega$ denote the exponent of matrix multiplication. Currently, $\omega \approx 2.373$. Let $\epsilon$ denote the accuracy error. In this paper, we make use of the input sparsity and purpose an algorithm that use $\log ( \|x_0 - x^*\|_2 / \epsilon)$ iterations and $\widetilde{O}(\mathrm{nnz}(A) + d^{\omega} )$ per iteration time to solve the problem.

Self-Supervised Modality-Aware Multiple Granularity Pre-Training for RGB-Infrared Person Re-Identification

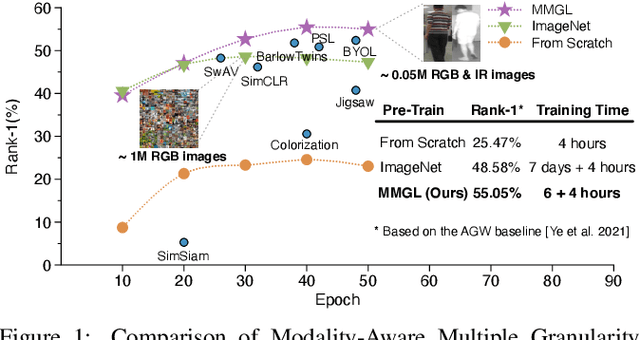
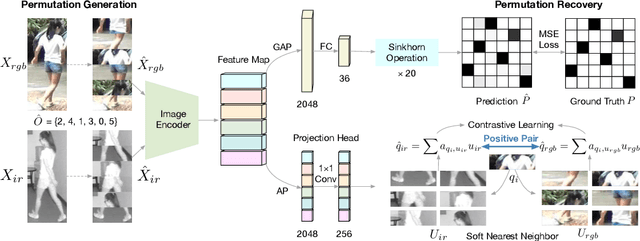
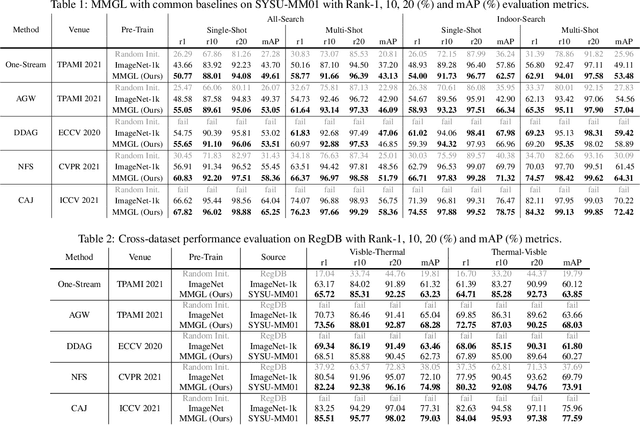
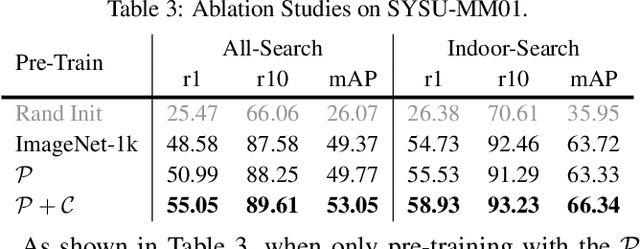
While RGB-Infrared cross-modality person re-identification (RGB-IR ReID) has enabled great progress in 24-hour intelligent surveillance, state-of-the-arts still heavily rely on fine-tuning ImageNet pre-trained networks. Due to the single-modality nature, such large-scale pre-training may yield RGB-biased representations that hinder the performance of cross-modality image retrieval. This paper presents a self-supervised pre-training alternative, named Modality-Aware Multiple Granularity Learning (MMGL), which directly trains models from scratch on multi-modality ReID datasets, but achieving competitive results without external data and sophisticated tuning tricks. Specifically, MMGL globally maps shuffled RGB-IR images into a shared latent permutation space and further improves local discriminability by maximizing agreement between cycle-consistent RGB-IR image patches. Experiments demonstrate that MMGL learns better representations (+6.47% Rank-1) with faster training speed (converge in few hours) and solider data efficiency (<5% data size) than ImageNet pre-training. The results also suggest it generalizes well to various existing models, losses and has promising transferability across datasets. The code will be released.

G$^2$DA: Geometry-Guided Dual-Alignment Learning for RGB-Infrared Person Re-Identification

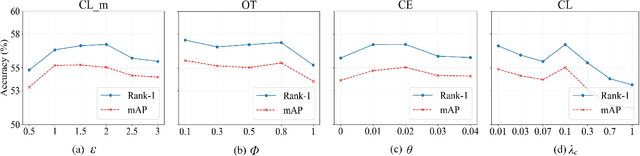
RGB-Infrared (IR) person re-identification aims to retrieve person-of-interest between heterogeneous modalities, suffering from large modality discrepancy caused by different sensory devices. Existing methods mainly focus on global-level modality alignment, whereas neglect sample-level modality divergence to some extent, leading to performance degradation. This paper attempts to find RGB-IR ReID solutions from tackling sample-level modality difference, and presents a Geometry-Guided Dual-Alignment learning framework (G$^2$DA), which jointly enhances modality-invariance and reinforces discriminability with human topological structure in features to boost the overall matching performance. Specifically, G$^2$DA extracts accurate body part features with a pose estimator, serving as a semantic bridge complementing the missing local details in global descriptor. Based on extracted local and global features, a novel distribution constraint derived from optimal transport is introduced to mitigate the modality gap in a fine-grained sample-level manner. Beyond pair-wise relations across two modalities, it additionally measures the structural similarity of different parts, thus both multi-level features and their relations are kept consistent in the common feature space. Considering the inherent human-topology information, we further advance a geometry-guided graph learning module to refine each part features, where relevant regions can be emphasized while meaningless ones are suppressed, effectively facilitating robust feature learning. Extensive experiments on two standard benchmark datasets validate the superiority of our proposed method, yielding competitive performance over the state-of-the-art approaches.

Neural Feature Search for RGB-Infrared Person Re-Identification

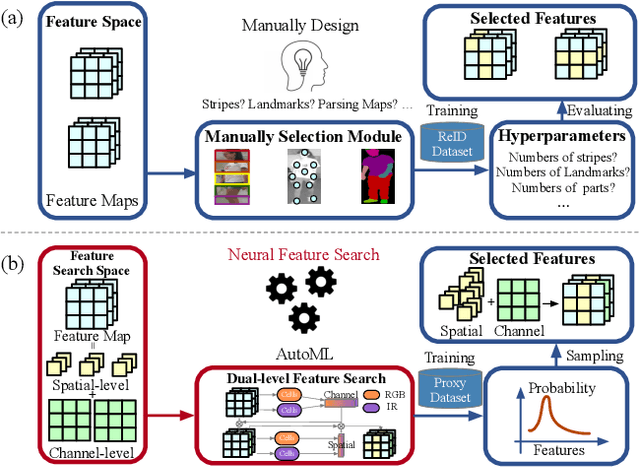
RGB-Infrared person re-identification (RGB-IR ReID) is a challenging cross-modality retrieval problem, which aims at matching the person-of-interest over visible and infrared camera views. Most existing works achieve performance gains through manually-designed feature selection modules, which often require significant domain knowledge and rich experience. In this paper, we study a general paradigm, termed Neural Feature Search (NFS), to automate the process of feature selection. Specifically, NFS combines a dual-level feature search space and a differentiable search strategy to jointly select identity-related cues in coarse-grained channels and fine-grained spatial pixels. This combination allows NFS to adaptively filter background noises and concentrate on informative parts of human bodies in a data-driven manner. Moreover, a cross-modality contrastive optimization scheme further guides NFS to search features that can minimize modality discrepancy whilst maximizing inter-class distance. Extensive experiments on mainstream benchmarks demonstrate that our method outperforms state-of-the-arts, especially achieving better performance on the RegDB dataset with significant improvement of 11.20% and 8.64% in Rank-1 and mAP, respectively.

ACFNet: Attentional Class Feature Network for Semantic Segmentation

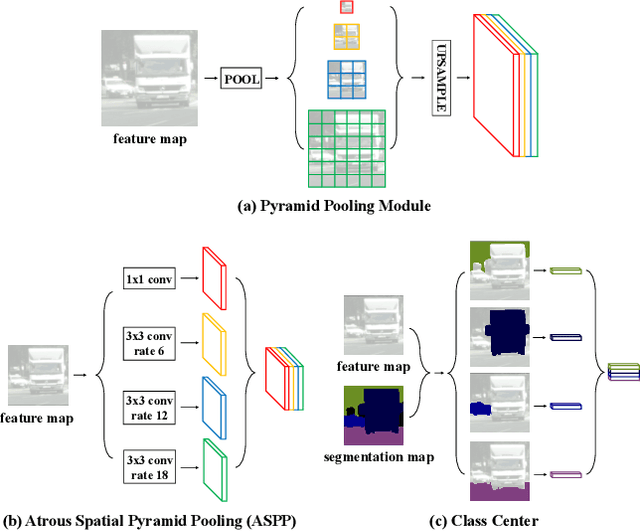
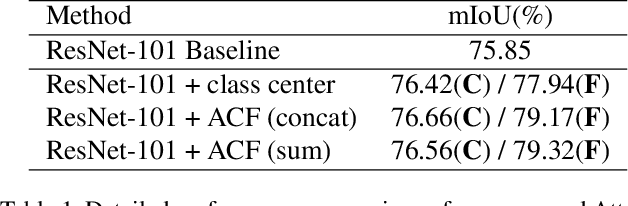
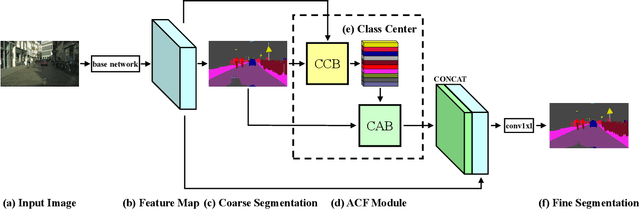
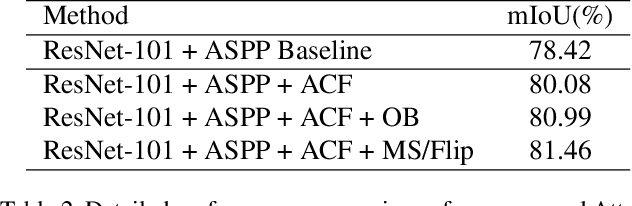
Recent works have made great progress in semantic segmentation by exploiting richer context, most of which are designed from a spatial perspective. In contrast to previous works, we present the concept of class center which extracts the global context from a categorical perspective. This class-level context describes the overall representation of each class in an image. We further propose a novel module, named Attentional Class Feature (ACF) module, to calculate and adaptively combine different class centers according to each pixel. Based on the ACF module, we introduce a coarse-to-fine segmentation network, called Attentional Class Feature Network (ACFNet), which can be composed of an ACF module and any off-the-shell segmentation network (base network). In this paper, we use two types of base networks to evaluate the effectiveness of ACFNet. We achieve new state-of-the-art performance of 81.85% mIoU on Cityscapes dataset with only finely annotated data used for training.

PyramidBox++: High Performance Detector for Finding Tiny Face

With the rapid development of deep convolutional neural network, face detection has made great progress in recent years. WIDER FACE dataset, as a main benchmark, contributes greatly to this area. A large amount of methods have been put forward where PyramidBox designs an effective data augmentation strategy (Data-anchor-sampling) and context-based module for face detector. In this report, we improve each part to further boost the performance, including Balanced-data-anchor-sampling, Dual-PyramidAnchors and Dense Context Module. Specifically, Balanced-data-anchor-sampling obtains more uniform sampling of faces with different sizes. Dual-PyramidAnchors facilitate feature learning by introducing progressive anchor loss. Dense Context Module with dense connection not only enlarges receptive filed, but also passes information efficiently. Integrating these techniques, PyramidBox++ is constructed and achieves state-of-the-art performance in hard set.