Better Understandings and Configurations in MaxSAT Local Search Solvers via Anytime Performance Analysis

Though numerous solvers have been proposed for the MaxSAT problem, and the benchmark environment such as MaxSAT Evaluations provides a platform for the comparison of the state-of-the-art solvers, existing assessments were usually evaluated based on the quality, e.g., fitness, of the best-found solutions obtained within a given running time budget. However, concerning solely the final obtained solutions regarding specific time budgets may restrict us from comprehending the behavior of the solvers along the convergence process. This paper demonstrates that Empirical Cumulative Distribution Functions can be used to compare MaxSAT local search solvers' anytime performance across multiple problem instances and various time budgets. The assessment reveals distinctions in solvers' performance and displays that the (dis)advantages of solvers adjust along different running times. This work also exhibits that the quantitative and high variance assessment of anytime performance can guide machines, i.e., automatic configurators, to search for better parameter settings. Our experimental results show that the hyperparameter optimization tool, i.e., SMAC, generally achieves better parameter settings of local search when using the anytime performance as the cost function, compared to using the fitness of the best-found solutions.

Impact of spatial transformations on landscape features of CEC2022 basic benchmark problems

When benchmarking optimization heuristics, we need to take care to avoid an algorithm exploiting biases in the construction of the used problems. One way in which this might be done is by providing different versions of each problem but with transformations applied to ensure the algorithms are equipped with mechanisms for successfully tackling a range of problems. In this paper, we investigate several of these problem transformations and show how they influence the low-level landscape features of a set of 5 problems from the CEC2022 benchmark suite. Our results highlight that even relatively small transformations can significantly alter the measured landscape features. This poses a wider question of what properties we want to preserve when creating problem transformations, and how to fairly measure them.

MA-BBOB: A Problem Generator for Black-Box Optimization Using Affine Combinations and Shifts

Choosing a set of benchmark problems is often a key component of any empirical evaluation of iterative optimization heuristics. In continuous, single-objective optimization, several sets of problems have become widespread, including the well-established BBOB suite. While this suite is designed to enable rigorous benchmarking, it is also commonly used for testing methods such as algorithm selection, which the suite was never designed around. We present the MA-BBOB function generator, which uses the BBOB suite as component functions in an affine combination. In this work, we describe the full procedure to create these affine combinations and highlight the trade-offs of several design decisions, specifically the choice to place the optimum uniformly at random in the domain. We then illustrate how this generator can be used to gain more low-level insight into the function landscapes through the use of exploratory landscape analysis. Finally, we show a potential use-case of MA-BBOB in generating a wide set of training and testing data for algorithm selectors. Using this setup, we show that the basic scheme of using a set of landscape features to predict the best algorithm does not lead to optimal results, and that an algorithm selector trained purely on the BBOB functions generalizes poorly to the affine combinations.

MA-BBOB: Many-Affine Combinations of BBOB Functions for Evaluating AutoML Approaches in Noiseless Numerical Black-Box Optimization Contexts

Extending a recent suggestion to generate new instances for numerical black-box optimization benchmarking by interpolating pairs of the well-established BBOB functions from the COmparing COntinuous Optimizers (COCO) platform, we propose in this work a further generalization that allows multiple affine combinations of the original instances and arbitrarily chosen locations of the global optima. We demonstrate that the MA-BBOB generator can help fill the instance space, while overall patterns in algorithm performance are preserved. By combining the landscape features of the problems with the performance data, we pose the question of whether these features are as useful for algorithm selection as previous studies suggested. MA-BBOB is built on the publicly available IOHprofiler platform, which facilitates standardized experimentation routines, provides access to the interactive IOHanalyzer module for performance analysis and visualization, and enables comparisons with the rich and growing data collection available for the (MA-)BBOB functions.

When to be Discrete: Analyzing Algorithm Performance on Discretized Continuous Problems

The domain of an optimization problem is seen as one of its most important characteristics. In particular, the distinction between continuous and discrete optimization is rather impactful. Based on this, the optimizing algorithm, analyzing method, and more are specified. However, in practice, no problem is ever truly continuous. Whether this is caused by computing limits or more tangible properties of the problem, most variables have a finite resolution. In this work, we use the notion of the resolution of continuous variables to discretize problems from the continuous domain. We explore how the resolution impacts the performance of continuous optimization algorithms. Through a mapping to integer space, we are able to compare these continuous optimizers to discrete algorithms on the exact same problems. We show that the standard $(\mu_W, \lambda)$-CMA-ES fails when discretization is added to the problem.

What Performance Indicators to Use for Self-Adaptation in Multi-Objective Evolutionary Algorithms

Parameter control has succeeded in accelerating the convergence process of evolutionary algorithms. Empirical and theoretical studies for classic pseudo-Boolean problems, such as OneMax, LeadingOnes, etc., have explained the impact of parameters and helped us understand the behavior of algorithms for single-objective optimization. In this work, by transmitting the techniques of single-objective optimization, we perform an extensive experimental investigation into the behavior of the self-adaptive GSEMO variants. We test three self-adaptive mutation techniques designed for single-objective optimization for the OneMinMax, COCZ, LOTZ, and OneJumpZeroJump problems. While adopting these techniques for the GSEMO algorithm, we consider different performance metrics based on the current non-dominated solution set. These metrics are used to guide the self-adaption process. Our results indicate the benefits of self-adaptation for the tested benchmark problems. We reveal that the choice of metrics significantly affects the performance of the self-adaptive algorithms. The self-adaptation methods based on the progress in one objective can perform better than the methods using multi-objective metrics such as hypervolume, inverted generational distance, and the number of the obtained Pareto solutions. Moreover, we find that the self-adaptive methods benefit from the large population size for OneMinMax and COCZ.

Using Affine Combinations of BBOB Problems for Performance Assessment

Benchmarking plays a major role in the development and analysis of optimization algorithms. As such, the way in which the used benchmark problems are defined significantly affects the insights that can be gained from any given benchmark study. One way to easily extend the range of available benchmark functions is through affine combinations between pairs of functions. From the perspective of landscape analysis, these function combinations smoothly transition between the two base functions. In this work, we show how these affine function combinations can be used to analyze the behavior of optimization algorithms. In particular, we highlight that by varying the weighting between the combined problems, we can gain insights into the effects of added global structure on the performance of optimization algorithms. By analyzing performance trajectories on more function combinations, we also show that aspects such as the scaling of objective functions and placement of the optimum can greatly impact how these results are interpreted.

Benchmarking Algorithms for Submodular Optimization Problems Using IOHProfiler

Submodular functions play a key role in the area of optimization as they allow to model many real-world problems that face diminishing returns. Evolutionary algorithms have been shown to obtain strong theoretical performance guarantees for a wide class of submodular problems under various types of constraints while clearly outperforming standard greedy approximation algorithms. This paper introduces a setup for benchmarking algorithms for submodular optimization problems with the aim to provide researchers with a framework to enhance and compare the performance of new algorithms for submodular problems. The focus is on the development of iterative search algorithms such as evolutionary algorithms with the implementation provided and integrated into IOHprofiler which allows for tracking and comparing the progress and performance of iterative search algorithms. We present a range of submodular optimization problems that have been integrated into IOHprofiler and show how the setup can be used for analyzing and comparing iterative search algorithms in various settings.

Non-Elitist Selection among Survivor Configurations can Improve the Performance of Irace

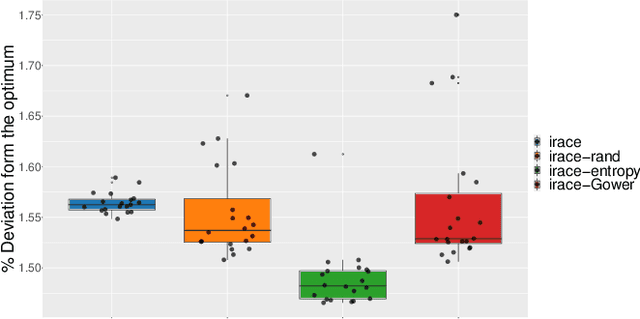
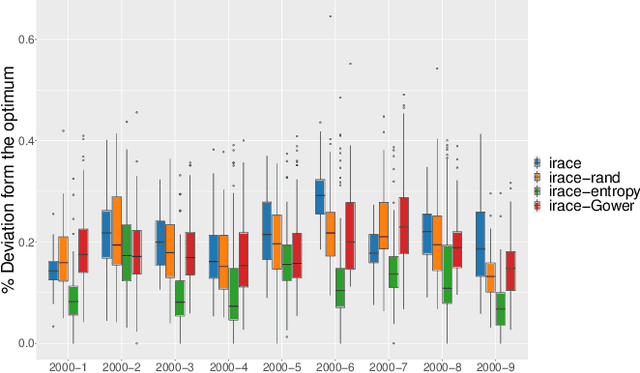
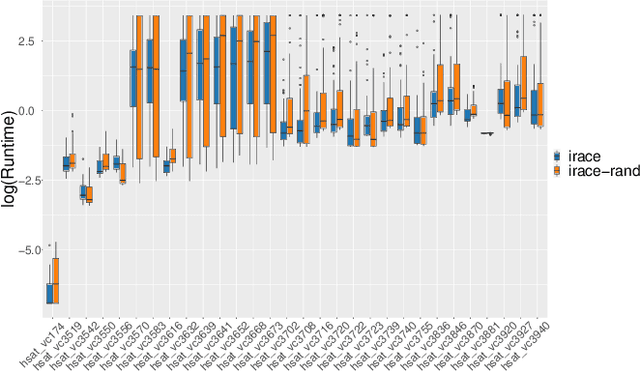
Modern optimization strategies such as evolutionary algorithms, ant colony algorithms, Bayesian optimization techniques, etc.~come with several parameters that steer their behavior during the optimization process. To obtain high-performing algorithm instances, automated algorithm configuration techniques have been developed. One of the most popular tools is irace, which evaluates configurations in sequential races, at the end of which a statistical test is used to determine the set of survivor configurations. It then selects up to five elite configurations from this set, via greedy truncation selection. We demonstrate that an alternative selection of the elites can improve the performance of irace. Our strategy keeps the best survivor and selects the remaining configurations uniformly at random from the set of survivors. We apply this alternative selection method to tune ant colony optimization algorithms for traveling salesperson problems and to configure an exact tree search solver for satisfiability problems. We also experiment with two non-elitist selection criteria, based on entropy and Gower's distance, respectively. Both methods provide more diverse configurations than irace, making them an interesting approach for exploring a wide range of solutions and understanding algorithms' performance. Moreover, the entropy-based selection performs better on our benchmarks than the default selection of irace.

IOHexperimenter: Benchmarking Platform for Iterative Optimization Heuristics

We present IOHexperimenter, the experimentation module of the IOHprofiler project, which aims at providing an easy-to-use and highly customizable toolbox for benchmarking iterative optimization heuristics such as evolutionary and genetic algorithms, local search algorithms, Bayesian optimization techniques, etc. IOHexperimenter can be used as a stand-alone tool or as part of a benchmarking pipeline that uses other components of IOHprofiler such as IOHanalyzer, the module for interactive performance analysis and visualization. IOHexperimenter provides an efficient interface between optimization problems and their solvers while allowing for granular logging of the optimization process. These logs are fully compatible with existing tools for interactive data analysis, which significantly speeds up the deployment of a benchmarking pipeline. The main components of IOHexperimenter are the environment to build customized problem suites and the various logging options that allow users to steer the granularity of the data records.