Mathematical Modeling and Convergence Analysis of Deep Neural Networks with Dense Layer Connectivities in Deep Learning

In deep learning, dense layer connectivity has become a key design principle in deep neural networks (DNNs), enabling efficient information flow and strong performance across a range of applications. In this work, we model densely connected DNNs mathematically and analyze their learning problems in the deep-layer limit. For a broad applicability, we present our analysis in a framework setting of DNNs with densely connected layers and general non-local feature transformations (with local feature transformations as special cases) within layers, which is called dense non-local (DNL) framework and includes standard DenseNets and variants as special examples. In this formulation, the densely connected networks are modeled as nonlinear integral equations, in contrast to the ordinary differential equation viewpoint commonly adopted in prior works. We study the associated training problems from an optimal control perspective and prove convergence results from the network learning problem to its continuous-time counterpart. In particular, we show the convergence of optimal values and the subsequence convergence of minimizers, using a piecewise linear extension and $\Gamma$-convergence analysis. Our results provide a mathematical foundation for understanding densely connected DNNs and further suggest that such architectures can offer stability of training deep models.

A Registration-Based Star-Shape Segmentation Model and Fast Algorithms

Image segmentation plays a crucial role in extracting objects of interest and identifying their boundaries within an image. However, accurate segmentation becomes challenging when dealing with occlusions, obscurities, or noise in corrupted images. To tackle this challenge, prior information is often utilized, with recent attention on star-shape priors. In this paper, we propose a star-shape segmentation model based on the registration framework. By combining the level set representation with the registration framework and imposing constraints on the deformed level set function, our model enables both full and partial star-shape segmentation, accommodating single or multiple centers. Additionally, our approach allows for the enforcement of identified boundaries to pass through specified landmark locations. We tackle the proposed models using the alternating direction method of multipliers. Through numerical experiments conducted on synthetic and real images, we demonstrate the efficacy of our approach in achieving accurate star-shape segmentation.

A Mathematical Explanation of UNet

The UNet architecture has transformed image segmentation. UNet's versatility and accuracy have driven its widespread adoption, significantly advancing fields reliant on machine learning problems with images. In this work, we give a clear and concise mathematical explanation of UNet. We explain what is the meaning and function of each of the components of UNet. We will show that UNet is solving a control problem. We decompose the control variables using multigrid methods. Then, operator-splitting techniques is used to solve the problem, whose architecture exactly recovers the UNet architecture. Our result shows that UNet is a one-step operator-splitting algorithm for the control problem.

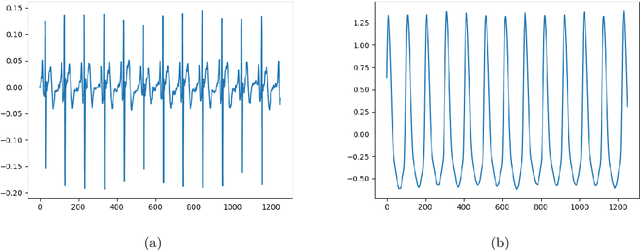
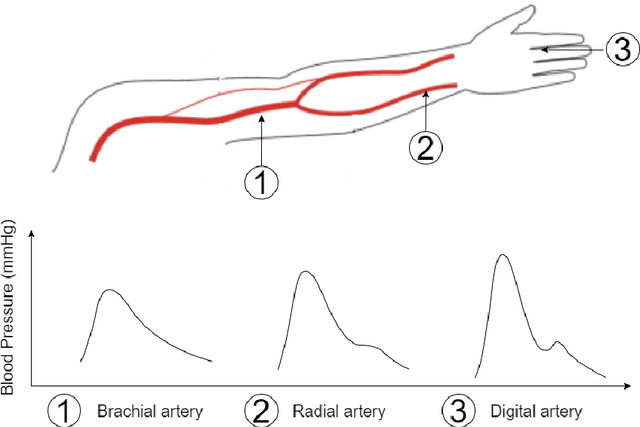
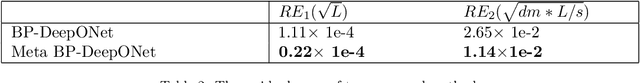
BP-DeepONet: A new method for cuffless blood pressure estimation using the physcis-informed DeepONet

Cardiovascular diseases (CVDs) are the leading cause of death worldwide, with blood pressure serving as a crucial indicator. Arterial blood pressure (ABP) waveforms provide continuous pressure measurements throughout the cardiac cycle and offer valuable diagnostic insights. Consequently, there is a significant demand for non-invasive and cuff-less methods to measure ABP waveforms continuously. Accurate prediction of ABP waveforms can also improve the estimation of mean blood pressure, an essential cardiovascular health characteristic. This study proposes a novel framework based on the physics-informed DeepONet approach to predict ABP waveforms. Unlike previous methods, our approach requires the predicted ABP waveforms to satisfy the Navier-Stokes equation with a time-periodic condition and a Windkessel boundary condition. Notably, our framework is the first to predict ABP waveforms continuously, both with location and time, within the part of the artery that is being simulated. Furthermore, our method only requires ground truth data at the outlet boundary and can handle periodic conditions with varying periods. Incorporating the Windkessel boundary condition in our solution allows for generating natural physical reflection waves, which closely resemble measurements observed in real-world cases. Moreover, accurately estimating the hyper-parameters in the Navier-Stokes equation for our simulations poses a significant challenge. To overcome this obstacle, we introduce the concept of meta-learning, enabling the neural networks to learn these parameters during the training process.

Double-well Net for Image Segmentation

In this study, our goal is to integrate classical mathematical models with deep neural networks by introducing two novel deep neural network models for image segmentation known as Double-well Nets. Drawing inspiration from the Potts model, our models leverage neural networks to represent a region force functional. We extend the well-know MBO (Merriman-Bence-Osher) scheme to solve the Potts model. The widely recognized Potts model is approximated using a double-well potential and then solved by an operator-splitting method, which turns out to be an extension of the well-known MBO scheme. Subsequently, we replace the region force functional in the Potts model with a UNet-type network, which is data-driven, and also introduce control variables to enhance effectiveness. The resulting algorithm is a neural network activated by a function that minimizes the double-well potential. What sets our proposed Double-well Nets apart from many existing deep learning methods for image segmentation is their strong mathematical foundation. They are derived from the network approximation theory and employ the MBO scheme to approximately solve the Potts model. By incorporating mathematical principles, Double-well Nets bridge the MBO scheme and neural networks, and offer an alternative perspective for designing networks with mathematical backgrounds. Through comprehensive experiments, we demonstrate the performance of Double-well Nets, showcasing their superior accuracy and robustness compared to state-of-the-art neural networks. Overall, our work represents a valuable contribution to the field of image segmentation by combining the strengths of classical variational models and deep neural networks. The Double-well Nets introduce an innovative approach that leverages mathematical foundations to enhance segmentation performance.

A Fast Minimization Algorithm for the Euler Elastica Model Based on a Bilinear Decomposition

The Euler Elastica (EE) model with surface curvature can generate artifact-free results compared with the traditional total variation regularization model in image processing. However, strong nonlinearity and singularity due to the curvature term in the EE model pose a great challenge for one to design fast and stable algorithms for the EE model. In this paper, we propose a new, fast, hybrid alternating minimization (HALM) algorithm for the EE model based on a bilinear decomposition of the gradient of the underlying image and prove the global convergence of the minimizing sequence generated by the algorithm under mild conditions. The HALM algorithm comprises three sub-minimization problems and each is either solved in the closed form or approximated by fast solvers making the new algorithm highly accurate and efficient. We also discuss the extension of the HALM strategy to deal with general curvature-based variational models, especially with a Lipschitz smooth functional of the curvature. A host of numerical experiments are conducted to show that the new algorithm produces good results with much-improved efficiency compared to other state-of-the-art algorithms for the EE model. As one of the benchmarks, we show that the average running time of the HALM algorithm is at most one-quarter of that of the fast operator-splitting-based Deng-Glowinski-Tai algorithm.

PottsMGNet: A Mathematical Explanation of Encoder-Decoder Based Neural Networks

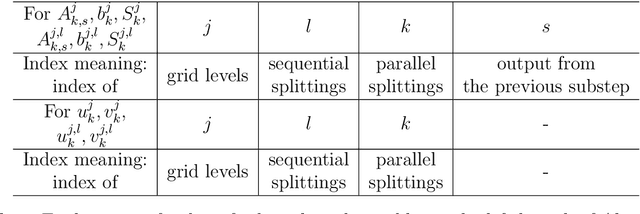
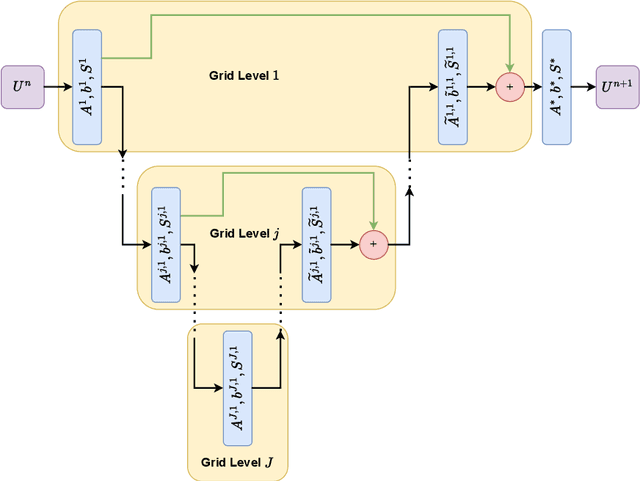
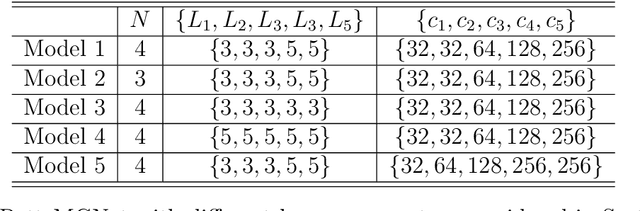
For problems in image processing and many other fields, a large class of effective neural networks has encoder-decoder-based architectures. Although these networks have made impressive performances, mathematical explanations of their architectures are still underdeveloped. In this paper, we study the encoder-decoder-based network architecture from the algorithmic perspective and provide a mathematical explanation. We use the two-phase Potts model for image segmentation as an example for our explanations. We associate the segmentation problem with a control problem in the continuous setting. Then, multigrid method and operator splitting scheme, the PottsMGNet, are used to discretize the continuous control model. We show that the resulting discrete PottsMGNet is equivalent to an encoder-decoder-based network. With minor modifications, it is shown that a number of the popular encoder-decoder-based neural networks are just instances of the proposed PottsMGNet. By incorporating the Soft-Threshold-Dynamics into the PottsMGNet as a regularizer, the PottsMGNet has shown to be robust with the network parameters such as network width and depth and achieved remarkable performance on datasets with very large noise. In nearly all our experiments, the new network always performs better or as good on accuracy and dice score than existing networks for image segmentation.

Connections between Operator-splitting Methods and Deep Neural Networks with Applications in Image Segmentation

Deep neural network is a powerful tool for many tasks. Understanding why it is so successful and providing a mathematical explanation is an important problem and has been one popular research direction in past years. In the literature of mathematical analysis of deep deep neural networks, a lot of works are dedicated to establishing representation theories. How to make connections between deep neural networks and mathematical algorithms is still under development. In this paper, we give an algorithmic explanation for deep neural networks, especially in their connection with operator splitting and multigrid methods. We show that with certain splitting strategies, operator-splitting methods have the same structure as networks. Utilizing this connection and the Potts model for image segmentation, two networks inspired by operator-splitting methods are proposed. The two networks are essentially two operator-splitting algorithms solving the Potts model. Numerical experiments are presented to demonstrate the effectiveness of the proposed networks.

Multiple Convex Objects Image Segmentation via Proximal Alternating Direction Method of Multipliers

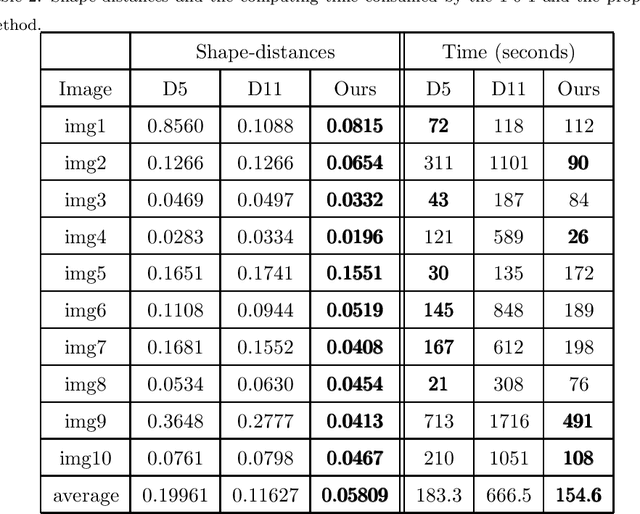
This paper focuses on the issue of image segmentation with convex shape prior. Firstly, we use binary function to represent convex object(s). The convex shape prior turns out to be a simple quadratic inequality constraint on the binary indicator function associated with each object. An image segmentation model incorporating convex shape prior into a probability-based method is proposed. Secondly, a new algorithm is designed to solve involved optimization problem, which is a challenging task because of the quadratic inequality constraint. To tackle this difficulty, we relax and linearize the quadratic inequality constraint to reduce it to solve a sequence of convex minimization problems. For each convex problem, an efficient proximal alternating direction method of multipliers is developed to solve it. The convergence of the algorithm follows some existing results in the optimization literature. Moreover, an interactive procedure is introduced to improve the accuracy of segmentation gradually. Numerical experiments on natural and medical images demonstrate that the proposed method is superior to some existing methods in terms of segmentation accuracy and computational time.

Elastica Models for Color Image Regularization

One classical approach to regularize color is to tream them as two dimensional surfaces embedded in a five dimensional spatial-chromatic space. In this case, a natural regularization term arises as the image surface area. Choosing the chromatic coordinates as dominating over the spatial ones, the image spatial coordinates could be thought of as a paramterization of the image surface manifold in a three dimensional color space. Minimizing the area of the image manifold leads to the Beltrami flow or mean curvature flow of the image surface in the 3D color space, while minimizing the elastica of the image surface yields an additional interesting regularization. Recently, the authors proposed a color elastica model, which minimizes both the surface area and elastica of the image manifold. In this paper, we propose to modify the color elastica and introduce two new models for color image regularization. The revised measures are motivated by the relations between the color elastica model, Euler's elastica model and the total variation model for gray level images. Compared to our previous color elastica model, the new models are direct extensions of Euler's elastica model to color images. The proposed models are nonlinear and challenging to minimize. To overcome this difficulty, two operator-splitting methods are suggested. Specifically, nonlinearities are decoupled by introducing new vector- and matrix-valued variables. Then, the minimization problems are converted to solving initial value problems which are time-discretized by operator splitting. Each subproblem, after splitting either, has a closed-form solution or can be solved efficiently. The effectiveness and advantages of the proposed models are demonstrated by comprehensive experiments. The benefits of incorporating the elastica of the image surface as regularization terms compared to common alternatives are empirically validated.