A Fast Minimization Algorithm for the Euler Elastica Model Based on a Bilinear Decomposition

The Euler Elastica (EE) model with surface curvature can generate artifact-free results compared with the traditional total variation regularization model in image processing. However, strong nonlinearity and singularity due to the curvature term in the EE model pose a great challenge for one to design fast and stable algorithms for the EE model. In this paper, we propose a new, fast, hybrid alternating minimization (HALM) algorithm for the EE model based on a bilinear decomposition of the gradient of the underlying image and prove the global convergence of the minimizing sequence generated by the algorithm under mild conditions. The HALM algorithm comprises three sub-minimization problems and each is either solved in the closed form or approximated by fast solvers making the new algorithm highly accurate and efficient. We also discuss the extension of the HALM strategy to deal with general curvature-based variational models, especially with a Lipschitz smooth functional of the curvature. A host of numerical experiments are conducted to show that the new algorithm produces good results with much-improved efficiency compared to other state-of-the-art algorithms for the EE model. As one of the benchmarks, we show that the average running time of the HALM algorithm is at most one-quarter of that of the fast operator-splitting-based Deng-Glowinski-Tai algorithm.

Fast Iterative Algorithms for Blind Phase Retrieval: A survey

In nanoscale imaging technique and ultrafast laser, the reconstruction procedure is normally formulated as a blind phase retrieval (BPR) problem, where one has to recover both the sample and the probe (pupil) jointly from phaseless data. This survey first presents the mathematical formula of BPR, related nonlinear optimization problems and then gives a brief review of the recent iterative algorithms. It mainly consists of three types of algorithms, including the operator-splitting based first-order optimization methods, second order algorithm with Hessian,and subspace methods. The future research directions for experimental issues and theoretical analysis are further discussed.

Bilinear Constraint based ADMM for Mixed Poisson-Gaussian Noise Removal

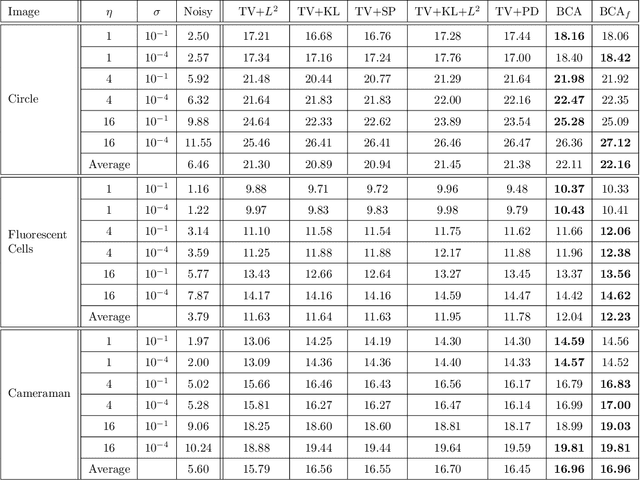
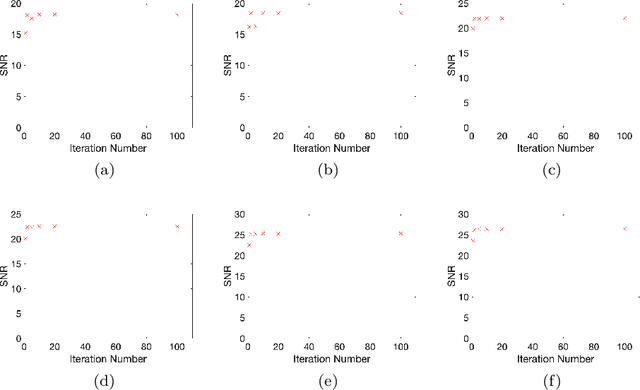
In this paper, we propose new operator-splitting algorithms for the total variation regularized infimal convolution (TV-IC) model in order to remove mixed Poisson-Gaussian (MPG) noise. In the existing splitting algorithm for TV-IC, an inner loop by Newton method had to be adopted for one nonlinear optimization subproblem, which increased the computation cost per outer loop. By introducing a new bilinear constraint and applying the alternating direction method of multipliers (ADMM), all subproblems of the proposed algorithms named as BCA (short for Bilinear Constraint based ADMM algorithm) and BCAf (short for a variant of BCA with fully splitting form) can be very efficiently solved; especially for the proposed BCAf , they can be calculated without any inner iterations. Under mild conditions, the convergence of the proposed BCA is investigated. Numerically, compared to existing primal-dual algorithms for the TV-IC model, the proposed algorithms, with fewer tunable parameters, converge much faster and produce comparable results meanwhile.